Участник:Anastasy/Алгоритм Диница: различия между версиями
Anastasy (обсуждение | вклад) |
Anastasy (обсуждение | вклад) |
||
| Строка 54: | Строка 54: | ||
=== Информационный граф === | === Информационный граф === | ||
| − | + | <div><ul> | |
| − | [[ | + | <li style="display: inline-block;"> [[File:dinic.png|thumb|none|500px|Информационный граф для алгоритма Диница]] </li> |
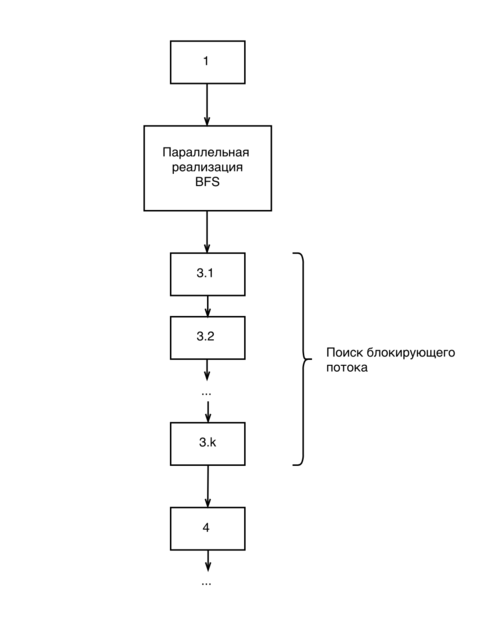
| + | <li style="display: inline-block;"> [[File:bfs.png|thumb|none|650px|Информационный граф для параллельной реализации поиска в ширину]] </li> | ||
| + | </ul></div> | ||
=== Ресурс параллелизма алгоритма === | === Ресурс параллелизма алгоритма === | ||
Версия 21:57, 27 ноября 2017
Алгоритм Диница
Автор: Киреева Анастасия, группа 416
Содержание
- 1 Постановка задачи
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Постановка задачи
1.1 Общее описание алгоритма
Алгоритм Диница [1] — полиномиальный алгоритм, предназначенный для поиска максимального потока в транспортной сети. Он был предложен советским учёным Ефимом Диницем в 1970 году. Временная сложность алгоритма O(nm^2), где m — число ребер, а n — число вершин.
Основная идея алгоритма состоит в том, чтобы итеративно увеличивать величину потока вдоль некоторых путей из истока в сток. Алгоритм Диница схож с алгоритмом Эдмондса-Карпа[2], но основное отличие можно понимать так: на каждой итерации поток увеличивается не вдоль одного кратчайшего пути из истока в сток, а вдоль целого набора таких путей.
1.2 Математическое описание алгоритма
Математическая постановка задачи приведена в статье "Поиск максимального потока в транспортной сети", мы будем использовать введённые в ней обозначения.
Введём необходимые определения.
Остаточной сетью G^R по отношению к сети G=(V, E) и некоторому потоку f в ней называется сеть, в которой каждому ребру (u,v) \in E с пропускной способностью c_{uv} и потоком f_{uv} соответствуют два ребра:
- (u,v) с пропускной способностью c_{uv}^R = c_{uv} - f_{uv}
- (v,u) с пропускной способностью c_{vu}^R = f_{uv}
Стоит отметить, что при таком определении в остаточной сети могут появляться кратные рёбра: если в исходной сети было как ребро (u,v), так и (v,u).
Блокирующим потоком в данной сети называется такой поток, что любой путь из истока s в сток t содержит насыщенное этим потоком ребро (то есть c_{uv} = f_{uv} для некоторых u,v \in V). Иными словами, в данной сети не найдётся такого пути из истока в сток, вдоль которого можно беспрепятственно увеличить поток.
Блокирующий поток не обязательно максимален. Согласно теореме Форда-Фалкерсона поток будет максимальным тогда и только тогда, когда в остаточной сети G^R не найдётся s-t пути; в блокирующем же потоке ничего не утверждается о существовании пути по рёбрам, появляющимся в остаточной сети.
Слоистая сеть для данной сети строится следующим образом. Сначала определяются длины кратчайших путей из истока s до всех остальных вершин; назовём уровнем {\rm level}[v] вершины её расстояние от истока. Тогда в слоистую сеть включают все те рёбра (u,v) исходной сети, для которых верно {\rm level}[u] + 1 = {\rm level}[v].
Слоистая сеть ациклична. Кроме того, любой s-t путь в слоистой сети является кратчайшим путём в исходной сети.
Алгоритм представляет собой несколько фаз. На каждой фазе сначала строится остаточная сеть, затем по отношению к ней строится слоистая сеть (обходом в ширину), а в ней ищется произвольный блокирующий поток. Найденный блокирующий поток прибавляется к текущему потоку, и на этом очередная итерация заканчивается. Алгоритм заканчивает свою работу, когда в построенной на некоторой итерации остаточной сети не найдётся s-t пути.
1.3 Вычислительное ядро алгоритма
Наибольший объем вычислений приходится на:
- поиск в ширину (для построения слоистой сети)
- обход в глубину (для построения блокирующего потока)
1.4 Макроструктура алгоритма
Одним из важных шагов алгоритма является поиск блокирующего потока. Опишем, каким образом это можно сделать.
Ищем s-t пути по одному обходом в глубину, пока такие пути находятся, при этом удаляем те ребра, вдоль которых невозможно дойти до стока. Для этого достаточно удалять ребро после того, как мы просмотрели его в обходе в глубину (кроме того случая, когда мы прошли вдоль ребра и нашли путь до стока). С точки зрения реализации, надо просто поддерживать в списке смежности каждой вершины указатель на первое неудалённое ребро, и увеличивать этот указатель в цикле внутри обхода в глубину.
1.5 Схема реализации последовательного алгоритма
Структуру алгоритма можно описать следующим образом:
- Для всех ребер (u, v) \in E сети G присвоим f_{uv}=0.
- Построим остаточную сеть G^R по отношению к сети G и потоку f. Затем строим слоистую сеть G^L по отношению к сети G^R. Если {\rm level}[t]=∞, алгоритм завершает работу и выводит поток f.
- Ищем блокирующий поток f' в сети G^R
- Прибавим f' к потоку f и переходим к шагу 2.
1.6 Последовательная сложность алгоритма
- С помощью поиска в ширину слоистая сеть строится за время O(m).
- Если обход в глубину достигает стока, насыщается как минимум одно ребро, иначе как минимум один указатель продвигается вперед. Таким образом, один запуск обхода в глубину работает за O(n + k), где k — число продвижения указателей. Ввиду того, что всего запусков обхода в глубину в рамках поиска одного блокирующего потока будет O(p), где p — число рёбер, насыщенных этим блокирующим потоком, то весь алгоритм поиска блокирующего потока отработает за O(pn + \sum\limits_i{k_i}). Учитывая, что все указатели в сумме прошли расстояние O(m), это дает асимптотику O(pn + pk). В худшем случае, когда блокирующий поток насыщает все рёбра, асимптотика получается O(mn).
- Можно показать, что после каждой итерации расстояние между стоком и истоком строго увеличивается[1] (то есть {\rm level'}[t] \gt {\rm level}[t], где {\rm level'}[t] — расстояние до стока, полученное на следующей итерации). Так как длина кратчайшего s-t пути не может превосходить n - 1, то и количество фаз алгоритма не превосходит n - 1. Таким образом, весь алгоритм Диница выполняется за O(n^2m).
1.7 Информационный граф
1.8 Ресурс параллелизма алгоритма
1.9 Входные и выходные данные алгоритма
Входные данные: Граф G(V, E). n вершин v_i и m ребер e_j = (v_j^{(1)}, v_j^{(2)}) с заданной пропускной способностью c_j, а также исток s и сток t.
Объем входных данных: O(m + n).
Выходные данные: величина максимального потока.
Объем выходных данных: O(1).
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
3 Литература
- ↑ Перейти обратно: 1,0 1,1 Диниц, Е. А. “Алгоритм решения задачи о максимальном потоке в сети со степенной оценкой.” Доклады АН СССР 194, no. 4 (1970): 754–57
- ↑ Edmonds, Jack; Karp, Richard M. (1972). "Theoretical improvements in algorithmic efficiency for network flow problems". Journal of the ACM. Association for Computing Machinery