Метод "Разделяй и властвуй" Завольсков/Землянский: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
| Строка 29: | Строка 29: | ||
&&&&&& b_{n-1} & a_{n} \\ | &&&&&& b_{n-1} & a_{n} \\ | ||
\end{bmatrix} | \end{bmatrix} | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
+ \begin{bmatrix} | + \begin{bmatrix} | ||
&&&&& \\ | &&&&& \\ | ||
Версия 18:36, 14 октября 2016
Авторы статьи: Завольсков Владислав, Землянский Роман, 614 группа
Содержание
- 1 ЧАСТЬ. Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 ЧАСТЬ. Программная реализация алгоритма
- 3 Литература
1 ЧАСТЬ. Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Метод разделяй и властвуй вычисления собственных значений и векторов трёхдиагональной матрицы - это наиболее быстрый из существующих методов, если нужны все собственные значения и собственные векторы трехдиагональной матриц, начиная с порядка n, примерно равного 26. (Точное значение этого порогового порядка зависит от компьютера.) Его численно устойчивая реализация весьма не тривиальна. В самом деле, хотя впервые метод был предложен еще в 1981 г., "правильный" способ его реализации был найден лишь в 1992 г. Этот способ воплощен LAPACK-программами ssyevd (для плотных матриц) и sstevd (для трехдиагональных матриц). В них стратегия "разделяй-и-влавствуй" используется для матриц порядка, большего чем 25. Для матриц меньшего порядка (или если нужны только собственные значения) происходит автоматический переход к QR-итерации.
1.2 Математическое описание алгоритма
Пусть
- L = \begin{bmatrix} a_{1} & b_{1}&&&&& \\ b_{1} & \ddots & \ddots \\ & \ddots & a_{m-1} & b_{m-1} \\ && b_{m-1} & a_{m} & b_{m} \\ &&& b_{m} & a_{m+1} & b_{m+1} \\ &&&& b_{m+1} & \ddots \\ &&&&&& \ddots & b_{n-1} \\ &&&&&& b_{n-1} & a_{n} \\ \end{bmatrix} = \begin{bmatrix} a_{1} & b_{1} &&&&& \\ b_{1} & \ddots & \ddots \\ & \ddots & a_{m-1} & b_{m-1} \\ && b_{m-1} & a_{m} - b_{m} \\ &&&& a_{m+1} - b_{m} & b_{m+1} \\ &&&& b_{m+1} & \ddots \\ &&&&&& \ddots & b_{n-1} \\ &&&&&& b_{n-1} & a_{n} \\ \end{bmatrix}
+ \begin{bmatrix} &&&&& \\ &&b_{m} & b_{m} \\ &&b_{m} & b_{m} \\ &&&&& \\ \end{bmatrix} =
- = \begin{bmatrix} T_{1} & 0 \\ 0 & T_{2}\end{bmatrix} + b_{m} * \begin{bmatrix} 0 \\ \vdots \\ 0 \\ 1 \\ 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix} \begin{bmatrix} 0 , \ldots , 0 , 1 , 1 , 0 \ldots , 0 \end{bmatrix} = \begin{bmatrix} T_{1} & 0 \\ 0 & T_{2}\end{bmatrix} + b_{m}vv^{T}
Предположим, что нам известны спектральные разложения матриц T_{1} и T_{2} : T_{i} = Q_{i} \Lambda_{i} Q_{i}^{T} . В действительности, они будут рекурсивно вычисляться тем же самым алгоритмом. Установим связь между собственными значениями матрицы Т и собственными значениями матриц T_{1} и T_{2}. Имеем:
T = \begin{bmatrix} T_{1} & 0 \\ 0 & T_{2}\end{bmatrix} + b_{m}vv^{T} = \begin{bmatrix} Q_{1} \Lambda_{1} Q_{1}^{T} & 0 \\ 0 & Q_{2} L_{2} Q_{2}^{T}\end{bmatrix} + b_{m}vv^{T} = \begin{bmatrix} Q_{1} & 0 \\ 0 & Q_{2}\end{bmatrix}(\begin{bmatrix} \Lambda_{1} & \\ & \Lambda_{2}\end{bmatrix} + b_{m}vv^{T})\begin{bmatrix} Q_{1}^{T} & 0 \\ 0 & Q_{2}^{T}\end{bmatrix} ,
где
u = \begin{bmatrix} Q_{1}^{T} & 0 \\ 0 & Q_{2}^{T}\end{bmatrix}v
так как v = \begin{bmatrix} 0 , \ldots , 0 , 1 , 1 , 0 \ldots , 0 \end{bmatrix}^T, получим матрицу, состоящую из последнего столбца матрицы Q_{1}^{T} и первого столбца матрицы Q_{2}^{T}.
Следовательно, T имеет те же собственные значения, что и пдобная ей матрица D + \rho uu^{T}, где D = \begin{bmatrix} L_{1} & 0 \\ 0 & L_{2}\end{bmatrix} - диагональная матрица, \rho = b_{m} - число, а u - вектор.
Будем предполагать, не ограничивая общности, что диагональные элементы d_{1}, \ldots, d_{n} матрицы D упорядочены по убыванию: d_{n} \lt = \ldots \lt =d_{1}.
Чтобы найти собственные значения матрицы D + \rho uu^{T}, вычислим её характеристический многочлен, считая пока матрицу D - \lambda I невырожденной. Тогда
det(D + \rho uu^{T} - \lambda I) = det((D - \lambda I)(I + \rho (D- \lambda I)^{-1} uu^{T})).
Поскольку D - \lambda I невырожденна, det(I + \rho (D - \lambda I)^{-1}uu^{T}) = 0 тогда и только тогда, когда \lambda - собственное значение. Заметим, что матрица I + \rho (D - \lambda I)^{-1}uu^{T} получается из единичной добавлением матрицы ранга 1. Определитель такой матрицы легко вычислить.
Лемма 1. Справедливо равенство det(I + xy^{T}) = 1 + y^{T}x, где x и y - векторы.
Таким образом,
det(I + \rho (D - \lambda I)^{-1}uu^{T}) = 1 + \rho u^{T}(D - \lambda I)^{-1}u
= 1 + \rho \sum_{i=1, n} \frac{u_{i}^{2}} {d_{i}-\lambda} = f(\lambda) ,
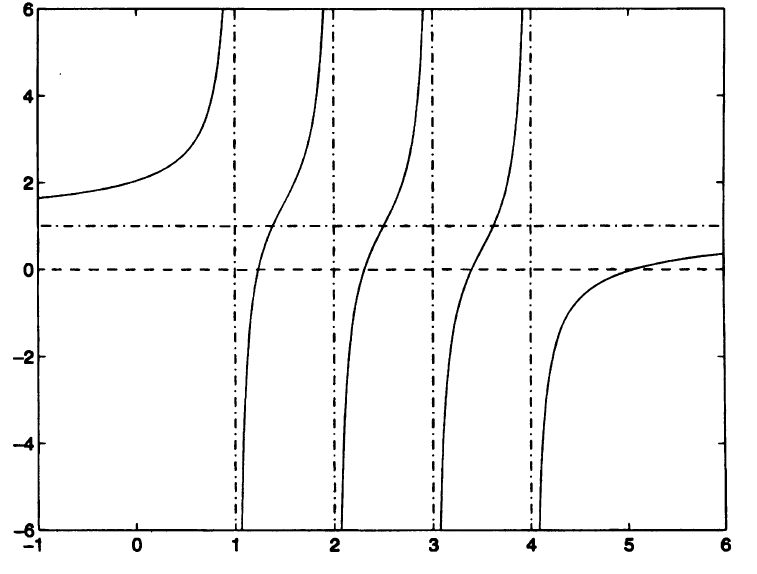
т.е. собственные значения матрицы T есть корни так называемого векового уравнения f(\lambda) = 0. Если все числа d_{i} различны и все u_{i} \lt \gt 0 (случай общего положения), то f(\lambda) имеет график типа показанного на рис. 1 (где n = 4 и \rho \gt 0).
Можно видеть, что прямая y = 1 является горизонтальной асимптотой для этого графика, а прямые \lambda = d_{i} есть вертикальные асимптоты. Поскольку f^{'}(\lambda) = \rho \sum_{i=1, n} \frac{u_{i}^{2}} {(d_{i}-\lambda)^{2}}\gt 0 , функция возрастает всюду, кроме точек \lambda = d_{i}. Поэтому корни функции разделяются числами d_{i} и ещё один корень находится справа от точки d_{1} (на рис. 1 d_{1} = 4). (При \rho\lt 0 функция f(\lambda) всюду убывает и соответствующий корень находится слева от точки d_{n}). Для функции f(\lambda), монотонной и гладкой на каждом из интервалов (d_{i+1},d_{i}), можно найти вариант метода Ньютона, который быстро и монотонно сходится к каждому из корней, если начальная точка взята в (d_{i+1},d_{i}). Нам достаточно знать, что на практике метод сходится к каждому собственному значению за ограниченное число шагов. Поскольку вычисление f(\lambda) и f^{'}(\lambda) стоит O(n) флопов, для вычисления одного собственного значения достаточно O(n), а для вычисления всех n собственных значений матрицы D + \rho uu^{T} требуется O(n^{2}) флопов. Для собственных векторов матрицы D + \rho uu^{T} мы легко можем получить явные выражения.
Лемма 2. Если \alpha - собственное значение матрицы D + \rho uu^{T}, то соответствующий вектор равен (D - \alpha I)^{-1}u. Поскольку матрица D - \alpha I диагональная, для вычисления такого вектора достаточно O(n) флопов.
Доказательство.
(D + \rho uu^{T})[(D - \alpha I)^{-1}u] = (D - \alpha I + \alpha I + \rho uu^{T})(D - \alpha I)^{-1}u
=u + \alpha (D - \alpha I)^{-1}u + u[\rho u^{T}(D - \alpha I)^{-1}u]
=u + \alpha(D - \alpha I)^{-1}u - u
поскольку [math] \rho u^{T}(D - \alpha I)^{-1}u + 1 = f(\alpha) = 0 [/math]
=\alpha [(D - \alpha I)^{-1}u], что и требовалось.
Для вычисления по этой простой формуле всех n собственных векторов требуется O(n^{2}) флопов. К сожалению, формула не обеспечивает численной устойчивости, так как для двух очень близких значений \alpha_{i} может давать неортогональные приближенные собственные векторы u_{i}. Потребовалось целое десятилетие для того, чтобы найти устойчивую альтернативу исходному описанию алгоритма. Снова детали будут обсуждаться позднее в данном разделе.
Алгоритм является рекурсивным.
1.3 Вычислительное ядро алгоритма
В описываемом алгоритме выделяется и описывается вычислительное ядро, т.е. та часть алгоритма, на которую приходится основное время работы алгоритма. Если в алгоритме несколько вычислительных ядер, то отдельно описывается каждое ядро. Описание может быть сделано в достаточно произвольной форме: словесной или с использованием языка математических формул. Вычислительное ядро может полностью совпадать с описываемым алгоритмом.
1.4 Макроструктура алгоритма
Сюда добавим про дефляцию и решение векового уравнения
1.5 Схема реализации последовательного алгоритма
Вычисление собственных значений и собственных векторов симметричной трехдиагональной матрицы посредством стратегии "разделяй и властвуй":
proc dc_eig(T,Q,\Lambda)... по входной матрице T вычисляются выходные матрицы Q и \Lambda, такие, что T = Q\Lambda Q^{T}
Если T - матрица размера 1 x 1
1. Присвоить выходным параметрам значения Q = 1, \Lambda = T
Иначе
1. Представить T в виде T = \begin{bmatrix} T_{1} & 0 \\ 0 & T_{2}\end{bmatrix} + b_{m}vv^{T}
2. call dc_eig(T_{1},Q_{1},\Lambda_{1})
3. call dc_eig(T_{2},Q_{2},\Lambda_{2})
4. Построить D+\rho uu^{T} по Lambda_{1},Lambda_{2}, Q_{1}, Q_{2}
5. Найти матрицу собственных значений \Lambda
6. Найти матрицу собственных векторов Q^{'} для матрицы D+\rho uu^{T}
7. Построить матрицу собственных векторов Q для матрицы T :
Q = \begin{bmatrix} Q_{1} & 0 \\ 0 & Q_{2}\end{bmatrix}* Q^{'}
8. Присвоить выходным параметрам значения Q и \Lambda
endif
1.6 Последовательная сложность алгоритма
Проанализируем сложность алгоритма. Пусть t(n) - число флопов при обработке матрицы размера n x n процедурой dc_eig. Тогда
t(n) = 2t(n/2) два рекурсивных обращения к dc_eig<(math>T_{i},Q_{i},\Lambda_{i})</math>
+O(n^{2}) вычисление собственных значений матрицы D+\rho uu^{T}
+O(n^{2}) вычисление собственных векторов матрицы D+\rho uu^{T}
+c*n^{3} вычисление матрицы Q = \begin{bmatrix} Q_{1} & 0 \\ 0 & Q_{2}\end{bmatrix}*Q^{'}
Если Q_{1}, Q_{2} и Q^{'} рассматриваются как плотные матрицы и используется стандартный алгоритм матричного умножения, то константа c в последней строке равна 1. Таким образом, именно это умножение составляет наиболее трудоёмкую часть алгоритма в целом. Игнорируя члены порядка n^{2}, получаем t(n) = 2t(n/2) + cn^{3}. Решая это разностное уравнение, находим t = c\frac{4}{3}n^{3}
На практике константа c обычно гораздо меньше 1, потому что матрица Q^{'} весьма разрежена вследствие явления, называемого дефляцией.
1.7 Информационный граф
TBD
1.8 Ресурс параллелизма алгоритма
TBD
1.9 Входные и выходные данные алгоритма
В данном разделе необходимо описать объем, структуру, особенности и свойства входных и выходных данных алгоритма: векторы, матрицы, скаляры, множества, плотные или разреженные структуры данных, их объем. Полезны предположения относительно диапазона значений или структуры, например, диагональное преобладание в структуре входных матриц, соотношение между размером матриц по отдельным размерностям, большое число матриц очень малой размерности, близость каких-то значений к машинному нулю, характер разреженности матриц и другие.
1.10 Свойства алгоритма
Какая-нибудь шляпа
2 ЧАСТЬ. Программная реализация алгоритма
Вторая часть описания алгоритмов в рамках AlgoWiki рассматривает все составные части процесса их реализации. Рассматривается как последовательная реализация алгоритма, так и параллельная. Описывается взаимосвязь свойств программ, реализующих алгоритм, и особенностей архитектуры компьютера, на которой они выполняются. Исследуется работа с памятью, локальность данных и вычислений, описывается масштабируемость и эффективность параллельных программ, производительность компьютеров, достигаемая на данной программе. Обсуждаются особенности реализации для разных классов архитектур компьютеров, приводятся ссылки на реализации в существующих библиотеках.
2.1 Масштабируемость алгоритма и его реализации
TBD
2.2 Существующие реализации алгоритма
TBD
3 Литература
[1] Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. - СПб.: БХВ-Петербург, 2002. - 608 с.
[2] Воеводин В.В., Воеводин Вад.В. Спасительная локальность суперкомпьютеров //Открытые системы. - 2013. - № 9. - С. 12-15.
[3] Воеводин Вад.В., Швец П. Метод покрытий для оценки локальности использования данных в программах // Вестник УГАТУ. — 2014. — Т. 18, № 1(62). — С. 224–229.
[4] Антонов А.С., Теплов А.М. О практической сложности понятия масштабируемости параллельных программ// Высокопроизводительные параллельные вычисления на кластерных системах (HPC 2014): Материалы XIV Международной конференции -Пермь: Издательство ПНИПУ, 2014. С. 20-27.
[5] Никитенко Д.А. Комплексный анализ производительности суперкомпьютерных систем, основанный на данных системного мониторинга // Вычислительные методы и программирование. 2014. 15. 85–97.