Участник:Lonalone/Генерация гауссовского вектора методом линейных преобразований: различия между версиями
Lonalone (обсуждение | вклад) |
Lonalone (обсуждение | вклад) |
||
| Строка 158: | Строка 158: | ||
=== Информационный граф === | === Информационный граф === | ||
| − | ==== Заполнение матрицы | + | ==== Заполнение матрицы B==== |
Граф алгоритма состоит из трёх групп вершин, расположенных в целочисленных узлах трёх областей разной размерности. | Граф алгоритма состоит из трёх групп вершин, расположенных в целочисленных узлах трёх областей разной размерности. | ||
| Строка 199: | Строка 199: | ||
Результат срабатывания операции является ''промежуточным данным'' алгоритма. | Результат срабатывания операции является ''промежуточным данным'' алгоритма. | ||
| − | Описанный граф можно посмотреть на рис.1 для случая <math>n = 4</math>. | + | Описанный граф можно посмотреть на рис.1, выполненном для случая <math>n = 4</math>. |
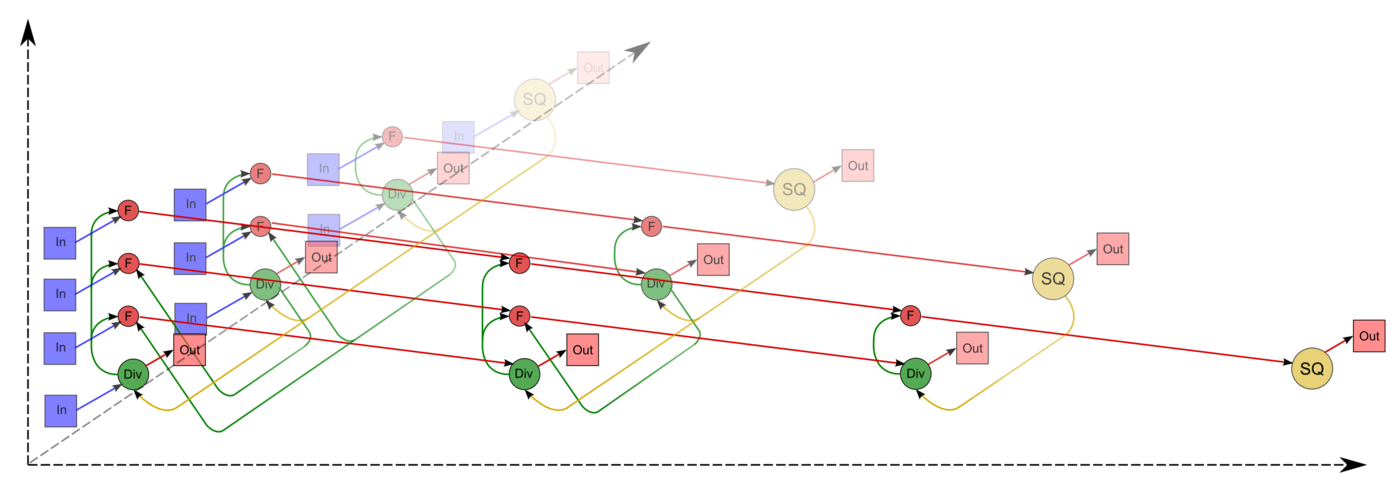
[[file:Cholesky full_in_out.png|thumb|center|1400px|Граф 1. SQ - вычисление квадратного корня, F - операция a-bc, Div - деление, In - входные данные, Out - результаты.]] | [[file:Cholesky full_in_out.png|thumb|center|1400px|Граф 1. SQ - вычисление квадратного корня, F - операция a-bc, Div - деление, In - входные данные, Out - результаты.]] | ||
| + | |||
| + | ====Генерация вектора Y==== | ||
| + | |||
| + | ====Вычисление вектора X==== | ||
| + | |||
| + | Граф алгоритма умножения плотной матрицы на вектор состоит из одной группы вершин, расположенной в целочисленных узлах двумерной области, соответствующая ей операция <math>a+bc</math>. | ||
| + | |||
| + | Естественно введённые координаты области таковы: | ||
| + | * <math>i</math> — меняется в диапазоне от <math>1</math> до <math>m</math>, принимая все целочисленные значения; | ||
| + | * <math>j</math> — меняется в диапазоне от <math>1</math> до <math>n</math>, принимая все целочисленные значения. | ||
| + | |||
| + | Аргументы операции следующие: | ||
| + | *<math>a</math>: | ||
| + | ** при <math>j = 1</math> константа <math>0.</math>; | ||
| + | ** при <math>j > 1</math> — результат срабатывания операции, соответствующей вершине с координатами <math>i, j-1</math>; | ||
| + | *<math>b</math> — элемент ''входных данных'', а именно <math>a_{ij}</math>; | ||
| + | *<math>c</math> - элемент входных данных <math>x_{j}</math>; | ||
| + | |||
| + | Результат срабатывания операции является: | ||
| + | * при <math>j < n</math> - ''промежуточным данным'' алгоритма; | ||
| + | * при <math>j = n</math> - выходным данным. | ||
| + | |||
| + | Описанный граф можно посмотреть на рисунке, выполненном для случая <math>m = 4, n = 5</math>. Здесь вершины обозначены голубым цветом. Изображена подача только входных данных из вектора <math>x</math>, подача элементов матрицы <math>A</math>, идущая во все вершины, на рисунке не представлена. | ||
| + | |||
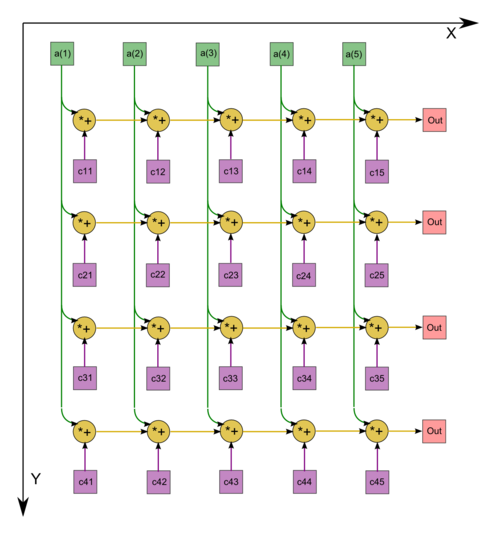
| + | [[Файл:YeqAX.png|500px|thumb|center|Рисунок 1. Граф 2]] | ||
=== Ресурс параллелизма алгоритма === | === Ресурс параллелизма алгоритма === | ||
Версия 19:49, 30 ноября 2018
Автор описания: Меньших И. М.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Из многомерных распределений особый интерес представляет нормальное. Этому закону подчиняются все результаты воздействия большого числа случайных факторов, среди которых нет превалирующих.
В статье приведен алгоритм генерации n-мерного гауссовского случайного вектора с помощью метода линейных преобразований[1]. Известно, что случае нормально распределенного случайного вектора, ковариационная матрица вместе с математическим ожиданием этого вектора полностью определяют его распределение. Поэтому для полного статистического соответствия моделируемого и теоретического распределения гауссовского вектора достаточно обеспечить требуемые значения указанных параметров[2].
Идея алгоритма заключается в линейном преобразовании n-мерного случайного вектора Y, компоненты которого независимы и одинаково распределены по нормальному закону со стандартными параметрами, в случайный вектор X с требуемыми ковариационной матрицей и вектором математических ожиданий.
1.2 Математическое описание алгоритма
1.2.1 Метод линейных преобразований
Даны ковариационная матрица \Sigma и вектор математических ожиданий M:
- \Sigma = \|\sigma_{ij}\| = \| \mathbb{E}[(X_{i} - m_{x_{i}})(X_{j} - m_{x_{j}})]\|, \\ M = (m_{x_{1}}, m_{x_{2}}, ..., m_{x_{n}})^T.
Требуется найти такую матрицу B, которая позволяла бы получить искомый вектор X с требуемыми характеристиками в результате линейного преобразования X = BY + M, где Y — n-мерный случайный вектор с независимыми нормально распределенными компонентами со стандартными параметрами.
Будем искать матрицу B в виде нижней треугольной матрицы. Перейдем от матричной записи к системе алгебраических уравнений:
- \begin{pmatrix} X_{1} \\ X_{2} \\ \vdots \\ X_{n} \end{pmatrix} = \begin{pmatrix} b_{11} & 0 & \cdots & 0 \\b_{21} & b_{22} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ b_{n1} & b_{n2} & \cdots & b_{nn} \end{pmatrix} \times \begin{pmatrix} Y_{1} \\ Y_{2} \\ \vdots \\ Y_{n} \end{pmatrix} + \begin{pmatrix} m_{x_{1}} \\ m_{x_{2}} \\ \vdots \\ m_{x_{n}} \end{pmatrix} \Rightarrow
- \begin{cases}X_{1} - m_{x_{1}} = b_{11}Y_{1} \\X_{2} - m_{x_{2}} = b_{21}Y_{1} + b_{22}Y_{2} \\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\X_{n} - m_{x_{n}} = b_{n1}Y_{1} + b_{n2}Y_{2} + \cdots + b_{nn}Y_{n} \end{cases}
Поскольку компоненты вектора Y независимы и имеют стандартные параметры, справедливо выражение:
- \mathbb{E}[Y_{i}Y_{j}] = \left\{\begin{matrix} 1, &i = j, \\ 0, &i \not= j. \end{matrix}\right.
Почленно перемножив сами на себя и между собой соответственно левые и правые части уравнений системы и взяв от результатов перемножения математическое ожидание, получаем систему уравнений вида:
- \begin{cases} \mathbb{E}[(X_{1} - m_{x_{1}})(X_{1} - m_{x_{1}})] = \mathbb{E}[b_{11}Y_{1}b_{11}Y_{1}], \\ \mathbb{E}[(X_{1} - m_{x_{1}})(X_{2} - m_{x_{2}})] = \mathbb{E}[(b_{21}Y_{1} + b_{22}Y_{2})b_{11}Y_{1}], \\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \end{cases}
Таким образом, в левых частях полученной системы уравнений располагаются элементы заданной ковариационной матрицы \Sigma, а в правых — элементы искомой матрицы B. Последовательно решая эту систему, получаем формулы для расчета элементов \sigma_{ij}:
- b_{11}=\sqrt{\sigma_{11}}; b_{21}=\frac{\sigma_{12}}{\sqrt{\sigma_{11}}}; b_{22} = \sqrt{\sigma_{22} - \frac{\sigma_{12}}{\sigma_{11}}}, \cdots
Рекуррентная формула для расчета любого элемента матрицы преобразования B имеет вид:
- b_{ij} = \frac {\sigma_{ij} - \sum_{k=1}^{j-1} b_{ik} b_{jk}} {\sqrt{\sigma_{ij} - \sum_{k=1}^{j-1} b_{jk}^2}}, \quad 1 \leqslant j \leqslant i \leqslant n
(суммы с верхним нулевым пределом считаются равными нулю)
Таким образом, матрица B получается с помощью разложения Холецкого матрицы \Sigma.
1.2.2 Генерация случайного вектора Y
Пусть имеется генератор псевдослучайных чисел (ГПСЧ, PRNG), с помощью которого можно получить реализацию случайной величины u \sim U(0,1) . Описанный выше случайный вектор Y=(y_1, \cdots, y_n) с независимыми компонентами составим из n реализаций случайной величины \eta \sim N(0,1). Каждую такую реализацию y_i, в свою очередь, получим с помощью приближения по ЦПТ \kappa случайными величинами, распределенными равномерно на отрезке [0,1]:
- y_i = \sqrt{\frac{12}{\kappa}} \left(\sum_{j=1}^{\kappa}{u_j^i} - \frac{\kappa}{2}\right), \quad i = \overline{1, n} \\
где u_j^i - реализации случайной величины u, а \kappa - параметр, обеспечивающий качество приближения.
Как правило, \kappa берут равным 12 и считают, что для подавляющего числа практических задач обеспечивается должная точность вычислений[3].
1.3 Вычислительное ядро алгоритма
\sigma_{ij} - \sum_{k=1}^{j-1} b_{ik} b_{jk}, \quad 1 \leqslant j \leqslant i \leqslant n
1.4 Макроструктура алгоритма
- Заполнение матрицы B
- Генерация вектора Y
- Вычисление вектора X = BY + M
1.5 Схема реализации последовательного алгоритма
1) Заполнение матрицы B.
- (a) b_{11}= \sqrt{\sigma_{11}}
- (b) b_{k1}= \frac{\sigma_{k1}}{l_{11}}, \quad k = \overline{2,n}
- Следующие два пункта выполняются циклически, друг за другом для i = \overline{2,n}.
- (c) b_{ii} = \sqrt{\sigma_{ii} - \sum_{p = 1}^{i - 1} b_{ip}^2}
- (d) b_{ji} = \frac{\sigma_{ji} - \sum_{p = 1}^{i - 1} b_{ip} b_{jp}} {l_{ii}}, \quad i \neq n, j = \overline{i+1,n}
2) Генерация вектора Y.
- Следующие два пункта выполняются циклически, друг за другом для i = \overline{1,n}.
- (a) u_j^i \leftarrow PRNG, \quad j = \overline{1,k}
- (b) y_i = \sqrt{\frac{12}{\kappa}} \left(\sum_{j=1}^{\kappa}{u_j^i} - \frac{\kappa}{2}\right)
3) Вычисление вектора X.
- x_i = m_{x_i} + \sum_{k = 1}^{i} b_{ik} y_{k}, \quad i = \overline{1,n}.
1.6 Последовательная сложность алгоритма
- \quad \frac {n(n-1)}{2} + \sum_{j=1}^{n-2}j(n-j-1) + n + \frac {n(n+1)}{2} = n(n+1) + \frac {n(n-1)(n-2)}{6} (умножений)
- \quad \frac {n(n-1)}{2} + \sum_{j=1}^{n-2}j(n-j-1) + n = \frac {n(n+1)}{2} + \frac {n(n-1)(n-2)}{6} (вычитаний)
- \quad (\kappa-1)n + \frac {n(n+1)}{2} = \frac {n(n-1+2\kappa)}{2} (сложений)
- \quad \frac {n(n-1)}{2} + 2n = \frac {n(n+3)}{2} (делений)
- \quad n + n = 2n (взятия квадратного корня)
\frac{n}{6}\left(2n^2+9n+31+6\kappa\right) - итого операций.
1.7 Информационный граф
1.7.1 Заполнение матрицы B
Граф алгоритма состоит из трёх групп вершин, расположенных в целочисленных узлах трёх областей разной размерности.
Первая группа вершин расположена в одномерной области, соответствующая ей операция вычисляет функцию SQRT. Единственная координата каждой из вершин i меняется в диапазоне от 1 до n, принимая все целочисленные значения.
Аргумент этой функции
- при i = 1 — элемент входных данных, а именно a_{11};
- при i \gt 1 — результат срабатывания операции, соответствующей вершине из третьей группы, с координатами i - 1, i, i - 1.
Результат срабатывания операции является выходным данным l_{ii}.
Вторая группа вершин расположена в двумерной области, соответствующая ей операция a / b. Естественно введённые координаты области таковы:
- i — меняется в диапазоне от 1 до n-1, принимая все целочисленные значения;
- j — меняется в диапазоне от i+1 до n, принимая все целочисленные значения.
Аргументы операции следующие:
- a:
- при i = 1 — элементы входных данных, а именно a_{j1};
- при i \gt 1 — результат срабатывания операции, соответствующей вершине из третьей группы, с координатами i - 1, j, i - 1;
- b — результат срабатывания операции, соответствующей вершине из первой группы, с координатой i.
Результат срабатывания операции является выходным данным l_{ji}.
Третья группа вершин расположена в трёхмерной области, соответствующая ей операция a - b * c. Естественно введённые координаты области таковы:
- i — меняется в диапазоне от 2 до n, принимая все целочисленные значения;
- j — меняется в диапазоне от i до n, принимая все целочисленные значения;
- p — меняется в диапазоне от 1 до i - 1, принимая все целочисленные значения.
Аргументы операции следующие:
- a:
- при p = 1 элемент входных данных a_{ji};
- при p \gt 1 — результат срабатывания операции, соответствующей вершине из третьей группы, с координатами i, j, p - 1;
- b — результат срабатывания операции, соответствующей вершине из второй группы, с координатами p, i;
- c — результат срабатывания операции, соответствующей вершине из второй группы, с координатами p, j;
Результат срабатывания операции является промежуточным данным алгоритма.
Описанный граф можно посмотреть на рис.1, выполненном для случая n = 4.
1.7.2 Генерация вектора Y
1.7.3 Вычисление вектора X
Граф алгоритма умножения плотной матрицы на вектор состоит из одной группы вершин, расположенной в целочисленных узлах двумерной области, соответствующая ей операция a+bc.
Естественно введённые координаты области таковы:
- i — меняется в диапазоне от 1 до m, принимая все целочисленные значения;
- j — меняется в диапазоне от 1 до n, принимая все целочисленные значения.
Аргументы операции следующие:
- a:
- при j = 1 константа 0.;
- при j \gt 1 — результат срабатывания операции, соответствующей вершине с координатами i, j-1;
- b — элемент входных данных, а именно a_{ij};
- c - элемент входных данных x_{j};
Результат срабатывания операции является:
- при j \lt n - промежуточным данным алгоритма;
- при j = n - выходным данным.
Описанный граф можно посмотреть на рисунке, выполненном для случая m = 4, n = 5. Здесь вершины обозначены голубым цветом. Изображена подача только входных данных из вектора x, подача элементов матрицы A, идущая во все вершины, на рисунке не представлена.
1.8 Ресурс параллелизма алгоритма
Для распараллеливания доступны следующие опции:
- вычисление элементов матрицы B в рамках столбца (под диагональю),
- генерация вектора Y,
- вычисление вектора X (умножение матрицы на вектор, сложение векторов).
1.9 Входные и выходные данные алгоритма
- Входные данные: вещественная всюду плотная положительно определенная симметрическая (n \times n) матрица \Sigma и вещественный (n) вектор M;
- Выходные данные: вещественный (n) вектор X.
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
// compute matrix B (core)
for (int j = 0; j < n; j++){
double sum_down = matrix_cov[j][j];
for (int k = 0; k < j; k++){
double cur = matrix_cov[j][k];
sum_down -= cur * cur;
}
matrix_cov[j][j] = sqrt(sum_down);
for (int i = j + 1; i < n; i++){
double sum_up = matrix_cov[i][j];
for (int k = 0; k < j; k++){
sum_up -= matrix_cov[i][k] * matrix_cov[j][k];
}
matrix_cov[i][j] = sum_up / matrix_cov[j][j];
}
}
// generate vector Y
for (int i = 0; i < n; i++){
double sum = generate_uniform(n);
for (int j = 0; j < CLT_NUM - 1; j++){
sum += generate_uniform(n);
}
vec_Y[i] = (sum - CLT_NUM / 2) * sqrt(12.0 / CLT_NUM);
}
// linear transformation
for (int i = 0; i < n; i++){
vec_X[i] = vec_exp[i];
for (int k = 0; k <= i; k++){
vec_X[i] += matrix_cov[i][k] * vec_Y[k];
}
}
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
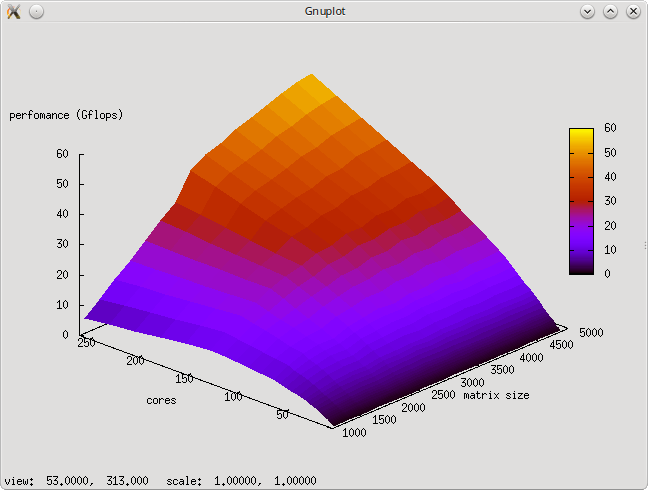
2.4 Масштабируемость алгоритма и его реализации
Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета. Алгоритм был реализован на языке C++ с использованием Intel MPI Library и запущен на кластере regular4.
Параметры компиляции и запуска:
module add slurm module add impi/5.0.1 mpicxx -std=c++0x task.c -o _scratch/task cd _scratch sbatch -n256 impi ./task <matrix_size>
Параметры запуска:
- размер матрицы [1024 : 4864] с шагом 256,
- число ядер [2 : 256] с шагом-умножением в 2 раза.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
В отличие от разложения Холецкого, которое реализовано (точечный метод) во многих прикладных пакетах (напр., LINPACK, LAPACK, SCALAPACK), моделирование гауссовского случайного вектора не так "популярно". MS Excel и распространённые статистические пакеты (напр., SPSS, Statistica) позволяют моделировать только одномерные статистические распределения.
Имеется возможность "собрать" многомерное распределение из нескольких одномерных при условии, что компоненты независимы. Однако если необходимо исследовать данные с зависящими друг от друга переменными, то приходится писать собственную программу.
3 Литература
- ↑ (п. 1.10.4) Михайлов Г.А., Войтишек А.В. Численное статистическое моделирование. Методы Монте-Карло — М.: Академия, 2006. — 368 с.
- ↑ https://ru.wikipedia.org/wiki/Многомерное_нормальное_распределение
- ↑ Балдин К.В., Уткин В.Б. Информационные системы в экономике. — М.:Дашков и Кo, 2008. — 395 с.