Участник:AleksLevin/Алгоритм Ланцоша вычисления собственных значений симметричной матрицы для точной арифметики (без переортогонализации)

Основные авторы описания: Левин А.Д. (студент, кафедра вычислительных методов, 604 группа)

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Данный алгоритм появился в 1950 г. и носит имя венгерского физика и математика Корнелия Ланцоша (венг. Lánczos Kornél). Алгоритм Ланцоша относится к итерационным методам вычисления собственных значений для матриц столь больших порядков $n$, что к ним нельзя применить прямые методы из-за ограничений по времени и памяти.

Сам Ланцош указывал, что его метод предназначен для отыскания нескольких собственных векторов симметричных матриц, хотя к методу сразу было обращено внимание, как к способу приведения всей матрицы к трёхдиагональному виду. Двадцатью годами позже канадский математик Крис Пэж показал, что, несмотря на чувствительность к округлениям, алгоритм Ланцоша - эффективное средство вычисления некоторых $k$ собственных чисел и соответствующих им собственных векторов [1, c.276]. Обычно число $k$ берут в два раза больше, чем количество собственных значений матрицы, которые поставлена цель найти, и оно имеет порядок не более $10^2$

Алгоритм Ланцоша для вычисления собственных значений симметричной матрицы $A$ соединяет в себе метод Ланцоша для построения последовательности подпространств Крылова и ортонормированных векторов Ланцоша и процедуру Рэлея-Ритца получения оптимальных приближений собственных значений и соответствующих собственных векторов исходной матрицы $A$ [2, с.381].

В данной статье рассматривается вариант алгоритма Ланцоша, в котором опущено влияние ошибок округления на вычислительный процесс, хотя на практике этому посвящается отдельное внимание и существуют различные методы решения данной проблемы, такие как частичная или полная переортогонализация. Этим модифицированным методам посвящены отдельные статьи на данном ресурсе.

1.2 Математическое описание алгоритма

Для лучшего понимания описания, данного в этом пункте статьи, рекомендуется ознакомиться с параграфом 6.6 Методы Крыловского подпространства [2, с.313]. Здесь же дано краткое описание всех переменных, математических операций и необходимый теоретический минимум.

Алгоритм Ланцоша для вычисления $k$ собственных значений и собственных векторов вещественной симметричной матрицы $A=A^T$ в точной арифметике [2, с.381]:

$\begin{align} q_1 = & \,\frac{b}{\|b\|_2},\; \beta_0 = 0,\; q_0 = 0\\ for \; & j = 1 \; to \; k \\ & z = A\,q_j\\ & \alpha_j = q^T_j z\\ & z = z - \alpha_j q_j - \beta_{j-1}q_{j-1}\\ & \beta_j = \|z\|_2\\ & If \; (\beta_j == 0) \; then\; stop\; the\; algorithm \\ & \; q_{j+1} = \frac{z}{\beta_j} \\ & compute\; eigenvalues\; and \;eigenvectors\;of \;matrix \;\;T_j= Q^T_j A Q\;\;and\;estimate \;the\; errors\\ end \; & for \end{align}$

В продемонстрированном выше алгоритме $b$ - заданный вещественный вектор. Также полагается известным алгоритм вычисления произведения матрицы $A$ на вектор $x$. Введём матрицу Крылова, определяемую следующим соотношением: $K_j = [b,Ab,A^2b,...,A^{j-1}b]$.

Далее, на практике, матрица $K$ заменяется матрицей $Q$, такой, что при любом числе $k$ линейные оболочки первых $k$ столбцов в $K$ и $Q$ являются одним и тем же подпространством [2, c.315]. Тогда матрица $Q$, в отличие от матрицы $K$, хорошо обусловлена и легко обратима. В результате получаем матрицу $Q_j = [q_1, q_2, \dots, q_j]$ размерности $n\times j$, столбцы которой ортогональны, являются базисом подпространства Крылова и называются векторами Ланцоша.

В алгоритме Ланцоша вычислению подлежит столько первых столбцов в матрице $Q_j$, сколько необходимо для получения требуемого приближения к решению $A\,x\,=b\,\,(A\,x=\lambda \, x)$.

Получение нулевого $\beta_j$ в итерационном процессе - событие, желательное в том смысле, что оно свидетельствует о том, что найдено некоторое подпространство, являющееся в точности инвариантным, а все собственные значения матрицы $T_j$ являются собственными значениями матрицы $A$. На практике же нулевое и близкие к нулю значения получаются редко [3, стр. 429].

Затем на каждом шаге цикла формируется симметричная трёхдиагональная матрица $T_j = Q^T_j A Q$, к которой применяется процесс Рэлея-Ритца для поиска её собственных значений (на практике для поиска этих собственных значений можно использовать любой из специальных методов, изложенных в [3, $\S$ 8.4]). Эти собственные значения, они же числа Ритца, и полагаются приближёнными собственными значениями исходной матрицы $A$.

Если требуется вычислить собственные векторы, то необходимо хранить вычисляемые векторы Ланцоша. Если работа при этом производится только с оперативной памятью, то при большом порядке исходной матрицы (а именно для таких матриц и предназначен метод Ланцоша) число шагов $j$, которые могут быть выполнены до того момента, как оперативная память будет исчерпана, будет очень незначительно, а следовательно, искомые собственные пары могут не успеть сойтись с требуемой точностью. В этом случае метод Ланцоша можно использовать итерационным образом: после выполнения заданного числа шагов процесс прерывается и, если еще не все требуемые пары Ритца сошлись с требуемой точностью, то формируется новый начальный вектор $q_1$, являющийся линейной комбинацией векторов Ритца, еще не сошедшихся с заданной точностью, и процесс начинается заново.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро рассматриваемого алгоритма (наиболее ресурсно-затратная часть алгоритма) - формирование на каждом шаге цикла промежуточного вектора $z$, вычисляемого по формуле: $z = A\,q_j$

1.4 Макроструктура алгоритма

Как уже было упомянуто в данной статье в описании алгоритма, рассматриваемый алгоритм состоит из двух последовательно выполненных алгоритмов: метод Ланцоша для построения последовательности подпространств Крылова и ортонормированных векторов Ланцоша и процедура Рэлея-Ритца получения оптимальных приближений собственных значений и соответствующих собственных векторов исходной матрицы.

В первой части алгоритма, где итерационно строятся Крыловское подпространство и трёхдиагональная матрица $T_j$, можно выделить следующие макрооперации:

• умножение матрицы на вектор (в свою очередь представляет собой умножение вектора на число и сложение векторов);
• вычисление нормы (скалярное произведение векторов + вычисление квадратного корня);
• скалярное произведение векторов;
• сложение векторов и их умножение на вещественные числа

Умножение матрицы на вектор - весьма дешевая и нетривиальная операция, если предполагать, что исходная матрица $A$ разреженная. Именно она подлежит оптимизации с использованием техник распараллеливания, поскольку она является вычислительным ядром алгоритма, а весь упомянутый процесс построения матрицы $T_j$ выполняется последовательно.

Вторая часть алгоритма - поиск собственных значений матрицы $T_j$, в нашем случае с помощью процедуры Рэлея-Ритца, может рассматриваться как отдельная нетривиальная макрооперация.

1.5 Схема реализации последовательного алгоритма

С целью полностью не дублировать пункт $\mathbf{1.2}$ данной статьи, где представлен очень наглядный и доступный для понимания псевдокод алгоритма, постараемся лишь коротко просуммировать и обобщить весь перечень последовательных действий в рассматриваемом алгоритме.

В качестве входных данных имеем: вещественная симметричная матрица $A$ размера $n\times n$, известный вещественный вектор $b$ длины $n$ и число $k\lt n$.

Далее:

• Инициализируем вещественную константу $\beta_0$ и векторы $q_0$ и $q_1$
• Итерационно для всех $j=\overline {1,k}$:
  • Вычисляем вспомогательный вектор $z$, используя умножение матрицы на вектор
  • Вычисляем, используя скалярное произведение векторов, значение $\alpha_j$ - элемент на главной диагонали трёхдиагональной матрицы $T_j$
  • Вычисляем по формуле новое значение и перезаписываем вектор $z$
  • Вычисляем значение $\beta_j$ - элементы непосредственно над и под главной диагональю той же матрицы $T_j$
  • Вычисляем с вектора $z$ очередной столбец матрицы $Q$, он же вектор Ланцоша : $\,\,q_{j+1}$
  • Теперь, когда матрица $T_j$ сформирована на очередном шаге, находим её собственные значения и вектора, например с помощью процедуры Рэлея-Ритца (о используемых на практике методах нахождения подробнее было сказано ранее в математическом описании алгоритма)
  • Переходим на следующую итерацию: $j$++

1.6 Последовательная сложность алгоритма

Оценим количество операций и сложность последовательного алгоритма, изложенного в предыдущем пункте.

• Для вычисления вектора $z$ умножается матрица размера $n\times n$ на вектор длины $n$, и потребуется $n^2$ операций умножения и $n^2$ операций сложения.
• Умножение векторов $q^T_j$ и $z$ длины $n$ потребует $n$ операций умножения и $n$ операций сложения.
• При вычислении нового значения вектора $z$ поэлементное сложение двух векторов длины $n$ требует $n$ операций сложения.
• Умножение вектора длины $n$ на вещественное число требует $n$ операций умножения.
• Нахождение квадратичной нормы вектора $z$ длины $n$ требует $n$ умножений и $n$ сложений и ещё 1 операцию извлечения квадратного корня.
• Заключительное нахождение собственных значений и собственных векторов трёхдиагональной матрицы $T_j$ размера $j\times j$ с помощью QR-алгоритма потребует в худшем случае $O(j^3)$ операций.

Посчитаем теперь суммарное количество простейших операций на одной итерации алгоритма (без учёта записей в память):

• $n^2+5\,n$ операций умножения/деления
• $n^2+4\,n$ операций сложения/вычитания
• 1 операция извлечения квадратного корня
  

Отдельно после всех итераций при $j=k$ :

• $O(k^3)$ операций для поиска собственных значений и собственных векторов трёхдиагональной матрицы $T_k$

Итого можно утверждать следующее:

Последовательная сложность одной итерации рассматриваемого алгоритма: $O(n ^ 2)$
Суммарная сложность алгоритма ($k$ итераций): $O(k\,n ^ 2) + O(k ^ 3)$

На практике же обычно рассматривается число $k\lt \lt n$, поэтому второе слагаемое можно опустить.

1.7 Информационный граф

На рисунке продемонстрирован граф одной итерации (при каком-либо произвольном значении итератора $j$) описанного алгоритма без отображения входных и выходных данных. Наглядно продемонстрированы связи между всеми действиями и с помощью деления на $n$ потоков показано, какие операции возможно выполнять параллельно на каждом шаге с целью оптимизации и экономии машинного времени. В результате, после параллельно выполненных операций Division на заключительном ярусе, на выходе имеем значение следующего вектора Ланцоша $q_{j+1}$, после чего следует переход на следующую итерацию, и процесс повторяется.

Simp (от англ. simple) - операции сложения и умножения вещественных чисел при вычислении произведения матрицы на вектор;

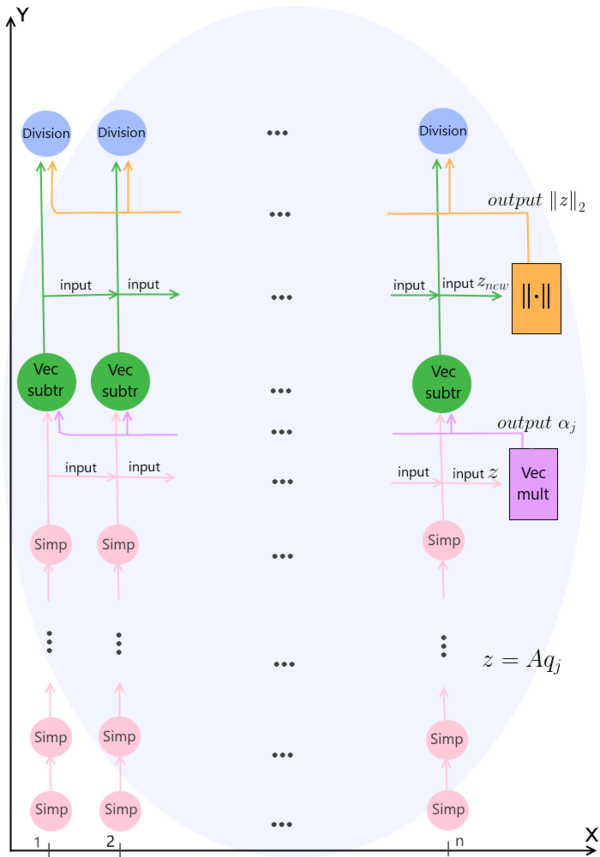
Vec mult (от англ. vectors multiplication) - операция скалярного умножения двух векторов;

Vec subtr (от англ. vectors subtraction, из-за использованных в операции вычитаний векторов) - операция умножения вектора на число (выполняется дважды) и формирование нового значения $z_{new}$ по формуле: $z = z - \alpha_j q_j - \beta_{j-1}q_{j-1}$

$||\cdot||$ - операция вычисления нормы вектора;

Division - операция деления вектора на вещественное число $\beta_j$

Важно отметить, что упомянутые выше операции также легко поддаются оптимизации. Например, попарные умножения вещественных координат векторов при вычислении скалярного произведения также легко выполняются параллельно на $n$ потоках, а затем можно применить суммирование методом сдваивания, о котором сказано в следующем пункте. Умножение или деление вектора на вещественное число являющееся, по определению, умножением или делением всех его координат на это число тоже может быть выполнено эффективнее, если мы используем $n$ потоков, а не выполняем эти действия последовательно.

1.8 Ресурс параллелизма алгоритма

Параллельные операции возможны только внутри итераций, так как рассматриваемый алгоритм является итерационным, и сами итерации строго последовательны.
Рассмотрим в этом пункте подробнее, какой выигрыш мы можем получить при распараллеливании операций внутри одной итерации согласно графу из предыдущего пункта.

Умножение вещественной симметричной матрицы $A$ размера $n\times n$ на вектор $b$ длины $n$ требует последовательного выполнения $n$ ярусов умножений и сложений. Сложение элементов вектора длины $n$ на каждом шаге перемножения можно оптимизировать и выполнить за $\log_2 n$ действий, если применять метод сдваивания.

Дальнейшие операции выполняются последовательно, а вычисление значений векторов происходит за один ярус операций сложения или умножения.

Ресурс параллелизма алгоритма вычисления собственных значений построенной трёхдиагональной матрицы $T_k$ размера $k\times k$ зависит от выбранного алгоритма (об этих алгоритмах подробнее было сказано в пункте 1.2). Будет очень затратно с точки зрения объёма материала пытаться рассмотреть пусть даже часть этих методов в этой статье, а так же тонкости их распараллеливания. Предлагаем читателям при желании самим ознакомиться с этими алгоритмами на данном ресурсе или прибегнув к иным источникам.

При классификации по высоте ЯПФ, таким образом, алгоритм Ланцоша без переортогонализации относится к алгоритмам с логарифмической сложностью, и его сложность равна $O(\log_2 n)$ с важным замечанием, что это сложность только одной итерации, а максимум в алгоритме может быть выполнено последовательно $k$ таких однотипных итераций.

Несмотря на то, что на графе в предыдущем пункте для лучшей визуализации и понимания было изображено $n$ потоков (никаких допущений мы не делали и нарушений с точки зрения логики и математики нет, можно изобразить большее число потоков, просто часть времени некоторые из них могут бездействовать и не использоваться), на самом деле правильным и разумным будет реализовать начальное параллельное выполнение $n^2$ операций умножения всех вещественных элементов матрицы $A$ на соответствующие элементы вектора $q_j$, после чего применять тот же самый упомянутый метод сдваивания.

Поэтому при классификации по ширине ЯПФ его сложность будет квадратичной и равна $O(n^2)$.

1.9 Входные и выходные данные алгоритма

Входные данные алгоритма: вещественная симметричная $A$ размера $n\times n$, вещественный вектор $b$ длины $n$, и одно вещественное число $k$, означающее количество итераций.

Объём входных данных: $n^2 +n + 1$. Если учесть, что матрица симметричная и достаточно для её однозначного определения задать элементы на главной диагонали и элементы над или под ней, то можно сократить объём входных данных с целью экономии памяти до: $\ \frac{n(n - 1)}{2} + n + 1$

Выходные данные алгоритма: вектор собственных значений $\Theta^k$ длины $k$, матрица из соответствующих собственных векторов $S^k$ размера $n\times k$.

Объём выходных данных: $k\;(n + 1)$.

1.10 Свойства алгоритма

добавить деммель страница 383 внизу

3 Литература

[1] Парлетт Б. - Симметричная проблема собственных значений. Численные методы //М.: Мир. - 1983. - С. 276-294

[2] James W. Demmel - Вычислительная линейная алгебра. Теория и приложения //Мир. - 2001. С. 381-391

[3] Голуб Дж., Ван Лоун Ч. - Матричные вычисления//М.: Мир. - 1999. - С. 426-436

[4] https://ru.wikipedia.org/wiki/Алгоритм_вычисления_собственных_значений#.D0.9C.D0.B0.D1.82.D1.80.D0.B8.D1.86.D1.8B_.D0.A5.D0.B5.D1.81.D1.81.D0.B5.D0.BD.D0.B1.D0.B5.D1.80.D0.B3.D0.B0_.D0.B8_.D1.82.D1.80.D1.91.D1.85.D0.B4.D0.B8.D0.B3.D0.BE.D0.BD.D0.B0.D0.BB.D1.8C.D0.BD.D1.8B.D0.B5_.D0.BC.D0.B0.D1.82.D1.80.D0.B8.D1.86.D1.8B

[5] http://num-anal.srcc.msu.ru/lib_na/int_ae/int_ae6.htm