Итерация алгоритма dqds

Алгоритм dqds нахождения сингулярных чисел двухдиагональной матрицы
Последовательный алгоритм
Последовательная сложность	$5n-4$
Объём входных данных	$2n$
Объём выходных данных	$2n$
Параллельный алгоритм
Высота ярусно-параллельной формы	$4n-3$
Ширина ярусно-параллельной формы	$2$

Основные авторы описания: А.Ю.Чернявский

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Итерация алгоритма dqds является одним шагом алгоритма dqds нахождения сингулярных чисел двухдиагональной матрицы.

Сам алгоритм dqds (differential quotient-difference algorithm with shifts) строит последовательность двухдиагональных матриц, сходящуюся к диагональной матрице, содержащей квадраты искомых сингулярных чисел. Его особенностью является высокая точность решения задачи. Вычислительным ядром алгоритма является именно внутренняя итерация, вне итераций происходит подбор сдвига $\delta$ (параметер итерации, см. математическое описание алгоритма), отслеживание сходимости, а также применение различных оптимизационных "хитростей". Отметим, что внеитерационная часть алгоритма не существенна с точки зрения структуры вычислений, т.к. основные затраты ложатся на вычисления внутри итерации. Подробности и варианты внеитерационной части, а также анализ сходимости можно найти в соответствующей литературе .

1.2 Математическое описание алгоритма

1.2.1 Вспомогательные сведения

Для понимания математических основ dqds-итерации полезно рассмотреть кратко её вывод, частично отражающий и историю возникновения алгоритма (подробности можно найти в ). За основу dqds-алгоритма удобно взять так называемую LR-итерацию, предшествующую хорошо-известной QR-итерации. LR-алгоритм, начиная с входной положительно определенной матрицы $T_0\gt 0,$ строит сходящуюся последовательность подобных $T_0$ матриц $T_i\gt 0,$ итерационно используя следующие три шага:

1. Выбрать сдвиг $\tau_i$ меньший младшего собственного значения $T_i.$
2. Вычислить разложение Холецкого $T_i-\tau^2_iI=B_i^TB_i,$ где $B_i$ - верхняя треугольная матрица с положительной диагональю.
3. $T_{i+1}=B_iB_i^T+\tau_i^2I.$

Отметим, что два шага LR-итерации с нулевым сдвигом эквивалентны одному шагу QR-итерации. Итерационная процедура приводит матрицу к диагональному виду, тем самым вычисляя собственные значения исходной матрицы. LR-алгоритм достаточно легко может быть переформулирован с заметными упрощениями для задачи поиска сингулярных значений двухдиагональных матриц. А именно, будем вычислять последовательность двухдиагональных матриц $B_i$ без непосредственного вычисления $T_i$(которые в данном случае будут трехдиагональными). Пусть матрица $B_i$ имеет диагональные элементы $a_1 \ldots a_n$ и наддиагональные элементы $b_1 \ldots b_{n-1}$, а матрица $B_{i+1}$ - диагональные элементы $\widehat{a}_1 \ldots \widehat{a}_n$ и наддиагональные элементы $\widehat{b}_1 \ldots \widehat{b}_{n-1}.$ Тогда шаг LR-итерации в терминах матриц $B_i$ можно привести к простому циклу, пробегающему значения $j$ от $1$ до $n-1:$

$\widehat{a}^2_j = a^2_j+b^2_j-\widehat{b}^2_{j-1}-\delta$

$\widehat{b}^2_j = b^2_j\dot (a^2_{j+1}/a^2_j)$

и вычислению $\widehat{a}^2_n = a^2_n-\widehat{b}^2_{n-1}-\delta.$ Очевидно, что работу с извлечением квадратов выгодно вести лишь после окончания работы алгоритма, поэтому можно ввести замену $q_j=a^2_j,\; e_j=b^2,$ что в итоге приводит к так называемому алгоритму qds. Формулы алгоритма следующие:

$\widehat{q}_j = q_j + e_j - \widehat{e}_{j-1} - \delta, \quad j \in [1,n-1]$

$\widehat{e}_j = e_j \cdot q_{j+1} / \widehat{q}_j, \quad j \in [1,n-1]$

$\widehat{q}_n = q_n - \widehat{e}_{n-1} - \delta.$

Здесь $q_j, \; j \in [1,n]$ и $e_j, \; j \in [1,n-1]$ - квадраты элемнтов главной и верхней побочной диагонали соответственно. Крышка означает выходные переменные, а

$\delta$ - сдвиг (параметр алгоритма). Такая математическая запись наиболее компактна и соответствует так называемой qds-итерации.

1.2.2 Математическое описание итерации алгоритма dqds

Представим теперь математическую запись, приближенную к dqds-итерации (с математической точки зрения qds и dqds-итерации эквивалентны) с введенными вспомогательными переменными

$t_j$ и $d_j.$ Итерация алгоритма dqds преобразует входную двухдиагональную матрицу $B$ в выходную $\widehat{B}.$

Входные и выходные данные: $q_{j}, \; j\in [1,n], \; e_{k}, \; k\in [1,n-1]$ - квадраты элементов главной и побочной диагонали входной матрицы $B$, $\widehat{q}_j , \; \widehat{e}_k$ - то же для вычисляемой матрицы $\widehat{B}.$.

Формулы метода выглядят следующим образом:

$d_1 = q_1 - \delta, \; q_n = d_n$

для$\quad j\in [1,n-1]:$

$\widehat{q}_j = d_j + e_j$

$t_j = q_{j+1}/\widehat{q}_j$

$\widehat{e}_j=e_j \cdot t_j$

$d_{j+1} = d \cdot t - \delta$

1.3 Вычислительное ядро алгоритма

Вычислительным ядром алгоритма является последовательный расчёт квадратов диагональных ($\widehat{q}_j$) и внедиагональных ($\widehat{e}_k$) элементов выходной матрицы. Учитывая использование вспомогательных переменных расчёт каждой новой пары содержит по одной операции сложения, вычитания и деления, а также две операции умножения.

1.4 Макроструктура алгоритма

Алгоритм состоит из отдельного вычисления начального значения вспомогательной переменной $d,$ последующим (n-1)-кратным выполнением повторяющейся последовательности из 5 операций (+,/,*,*,-) для вычисления квадратов диагональных ($\widehat{q}_j$) и внедиагональных ($\widehat{e}_k$) элементов выходной матрицы и завершающего вычислением крайнего значения $\widehat{q}_n$.

1.5 Схема реализации последовательного алгоритма

Отметим, что выходные данные сразу могут быть записаны на место входных (это учтено в схеме), также для хранения вспомогательных переменных $t_j$ и $d_j$ достаточно двух перезаписываемых переменных. Таким образом элементы главной ($q_j$) и побочной ($e_k$) диагонали входной матрицы последовательно перезаписываются соответствующими элементами выходной матрицы.

Последовательность исполнения метода следующая:

1. Вычисляется начальное значение вспомогательной переменной $d = q_1-\delta.$

2. Производится цикл по j от 1 до n-1, состоящий из:

2.1 Вычисляется значение $q_j = d + e_j;$

2.2 Вычисляется значение вспомогательной переменной $t = q_{j+1}/q_j;$

2.3 Вычисляется значение $e_j = e_j \cdot t;$

2.4 Вычисляется значение вспомогательной переменной $d = d \cdot t - \delta.$

3. Вычисляется $q_n = d.$

Легко заметить, что можно представить вычисления в другой форме, например, в виде qds-итерации (см. Математическое описание dqds-итерации), однако, именно dqds реализация вычисления позволяет достичь высокой точности.

1.6 Последовательная сложность алгоритма

Для выполнения одной итерации dqds необходимо выполнить:

• $n-1$ делений,
• $2n-2$ умножений,
• $2n-1$ сложений/вычитаний.

Таким образом одна dqds-итерация имеет линейную сложность.

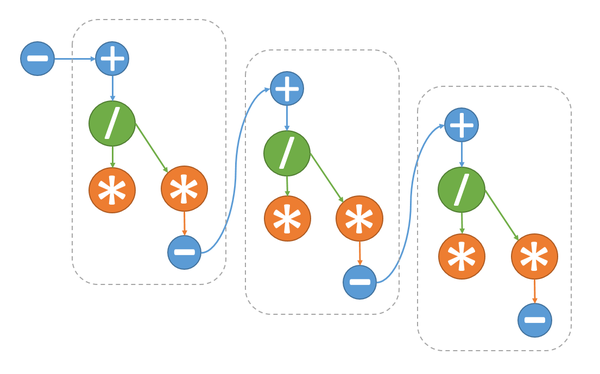
1.7 Информационный граф

Рисунок 1. Граф алгоритма для n=4 без отображения входных и выходных данных.

1.8 Ресурс параллелизма алгоритма

Как видно из информационного графа алгоритма, на каждом шаге основного цикла возможно лишь параллельное выполнение операции умножения (2.2) и умножения+сложения (2.4). Это позволяет сократить число ярусов на одной итерации цикла c 5 до 4, а общее число ярусов алгоритма с 5n-4 до 4n-3. Ярусы с операциями умножения состоят из двух операций, остальные же из одной.

1.9 Входные и выходные данные алгоритма

Входные данные: Квадраты элементов основной и верхней побочной диагонали двухдиагональной матрицы (вектора $q$ длины n и $e$ длины n-1), а также параметр сдвига $\delta$.

Объём входных данных: $2n$.

Выходные данные: Квадраты элементов основной и верхней побочной диагонали выходной двухдиагональной матрицы.

Объём выходных данных: $2n-1$.

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности при наличии возможности параллельного выполнения операций умножения составляет $\frac{5n-4}{4n-3}$, т.е. алгоритм плохо распараллеливается.

Вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных - константа.

Описываемый алгоритм является полностью детерминированным.

2 Программная реализация алгоритмов

2.1 Особенности реализации последовательного алгоритма

Алгоритм на языке Matlab может быть записать так:

d = q(1)-delta;
for j = 1:n-1
    q(j)=d+e(j);
    t=q(j+1)/q(j);
    e(j) = e(j)*t;
    d = d*t-delta;
end
q(n) = d;

Как говорилось в cхеме реализации последовательного алгоритма, вычисляемые данные записываются сразу на место входных.

2.2 Локальность данных и вычислений

Легко видеть, что локальность данных высока. Её легко повысить, размещая рядом соответствующие элементы массивов e и q, однако, это не оказывает существенного влияния на производительность в силу константного количества операций относительно объема обрабатываемых данных.

2.2.1 Локальность реализации алгоритма

2.2.1.1 Структура обращений в память и качественная оценка локальности

Рисунок 2. Итерация алгоритма dqds. Общий профиль обращений в память

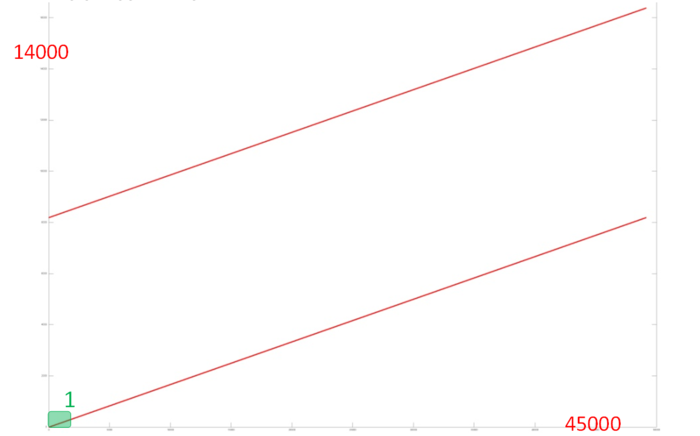
На рис. 2 представлен профиль обращений в память для реализации итерации алгоритма dqds. Данный профиль внешне устроен очень просто и состоит из двух параллельно выполняемых последовательных переборов. Отметим, что общее число обращений в память всего в 3 раза больше числа задействованных данных, что говорит о том, что данные повторно используют редко. Зачастую это сигнализирует о достаточно невысокой локальности.

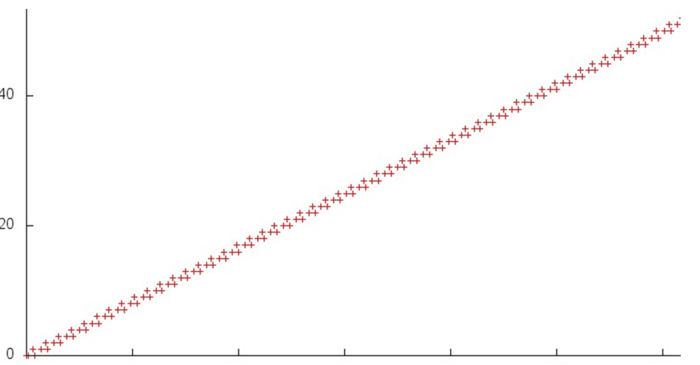
Рассмотрим более детально строение одного из переборов (второй устроен практически идентично). На рис. 3 показан выделенный на рис. 2 небольшой фрагмент 1. Видно, что на каждом шаге в данном переборе выполняется три обращения в память; подобное строение говорит о высокой пространственной локальности, однако низкой временной, поскольку данные повторно используются только по 3 раза.

Поскольку данная структура обращений и составляет общий профиль, то же самое можно говорить и о локальности всего профиля.

Рисунок 3. Профиль обращений, фрагмент 1

2.2.1.2 Количественная оценка локальности

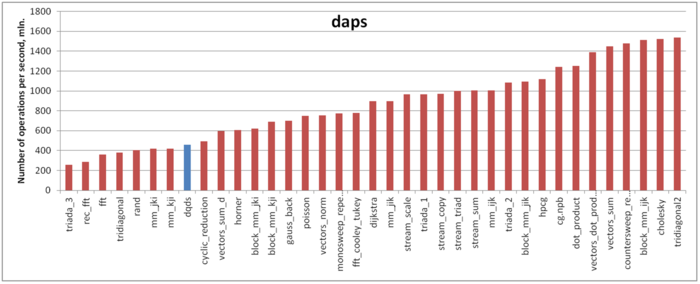
Оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.

На рисунке 4 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Результат получен достаточно неожиданный – производительность работы с памятью очень невелика. Оценка daps для данного профиля сравнима с реализациями самых неэффективных алгоритмов в части работы с памятью – тестов RandomAccess и неэффективных вариантов обычного перемножения матриц. Отчасти это может объясняться низкой временной локальностью. Однако в данном случае причина может также заключаться в том, что в данной реализации объем вычислений на одно обращение в память достаточно велик, что может приводить к недостаточной загруженности подсистемы памяти. В таком случае, несмотря на в целом неплохую эффективность работы с памятью, производительность будет достаточно низка.

Рисунок 4. Сравнение значений оценки daps

2.3 Возможные способы и особенности параллельной реализации алгоритма

Итерация dqds практически полностью последовательна. Единственная возможность - одновременное выполнение операции умножения (2.3) и операции (2.4) умножения и сложения, что дает небольшой выигрыш в производительности.

2.4 Масштабируемость алгоритма и его реализации

Алгоритм не является масштабируемым, максимального эффекта ускорения можно добиться на двух независимых процессорах.

Проведём исследование масштабируемости вширь реализации согласно методике. Исследование проводилось на суперкомпьютере "Ломоносов-2" Суперкомпьютерного комплекса Московского университета.

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

• число процессоров 1;
• размер матрицы [1000 : 260000] с шагом 500.

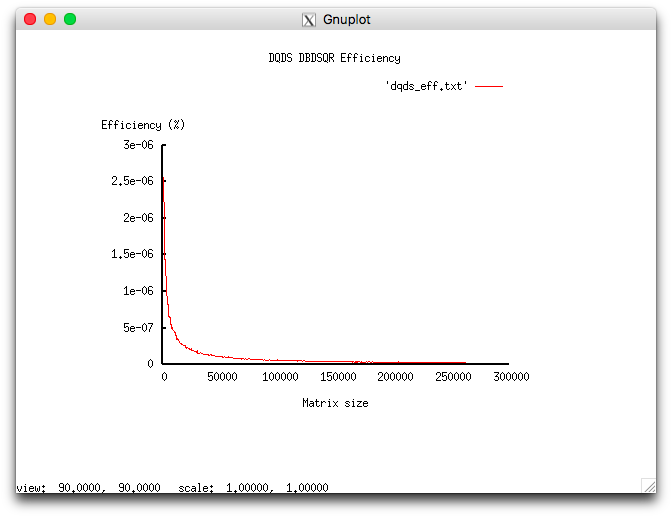
В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма:

• минимальная эффективность реализации 2.559e-06%;
• максимальная эффективность реализации 2.492e-08%.

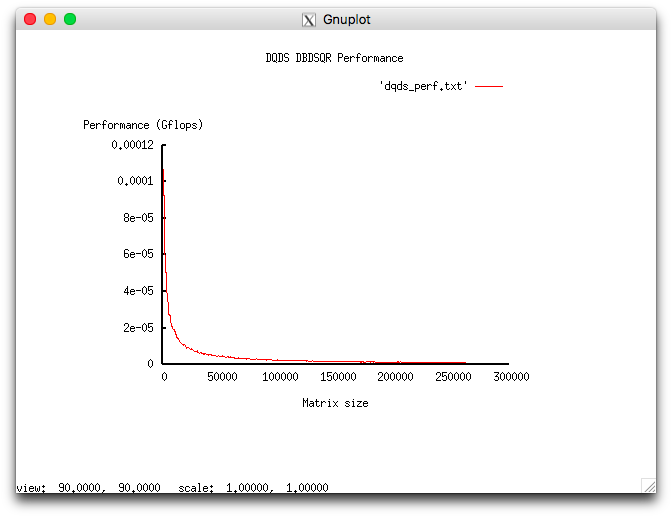
На следующих рисунках приведены графики производительности и эффективности выбранной реализации DQDS в зависимости от изменяемых параметров запуска.

Рисунок 8. Параллельная реализация алгоритма dqds. Изменение производительности в зависимости от числа процессоров и размера матрицы.

Рисунок 9. Параллельная реализация алгоритма dqds. Изменение эффективности в зависимости от числа процессоров и размера матрицы.

Исследованная параллельная реализация на языке C

2.5 Выводы для классов архитектур

Эффективное выполнение алгоритма возможно только на вычислительных устройствах с одним или двумя ядрами.

2.6 Существующие реализации алгоритма

Сам алгоритм dqds реализован в функции xBDSQR пакета LAPACK и используется при её вызове без расчёта сингулярных векторов.