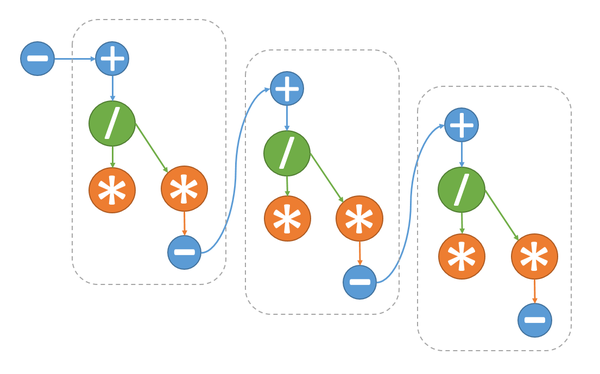
Итерация алгоритма dqds
| Алгоритм dqds нахождения сингулярных чисел двухдиагональной матрицы | |
| Последовательный алгоритм | |
| Последовательная сложность | 5n-4 |
| Объём входных данных | 2n |
| Объём выходных данных | 2n |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | 4n-3 |
| Ширина ярусно-параллельной формы | 2 |
Основные авторы описания: А.Ю.Чернявский
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритмов
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Итерация алгоритма dqds является одним шагом алгоритма dqds нахождения сингулярных чисел двухдиагональной матрицы.
Сам алгоритм dqds (differential quotient-difference algorithm with shifts)[1][2] строит последовательность двухдиагональных матриц, сходящуюся к диагональной матрице, содержащей квадраты искомых сингулярных чисел. Его особенностью является высокая точность решения задачи. Вычислительным ядром алгоритма является именно внутренняя итерация, вне итераций происходит подбор сдвига \delta (параметер итерации, см. математическое описание алгоритма), отслеживание сходимости, а также применение различных оптимизационных "хитростей". Отметим, что внеитерационная часть алгоритма не существенна с точки зрения структуры вычислений, т.к. основные затраты ложатся на вычисления внутри итерации. Подробности и варианты внеитерационной части, а также анализ сходимости можно найти в соответствующей литературе [3] [4] [5].
1.2 Математическое описание алгоритма
1.2.1 Вспомогательные сведения
Для понимания математических основ dqds-итерации полезно рассмотреть кратко её вывод, частично отражающий и историю возникновения алгоритма (подробности можно найти в [1]). За основу dqds-алгоритма удобно взять так называемую LR-итерацию, предшествующую хорошо-известной QR-итерации. LR-алгоритм, начиная с входной симметричной и положительно определенной матрицы T_0\gt 0, строит сходящуюся последовательность подобных T_0 матриц T_i\gt 0, итерационно используя следующие три шага:
- Выбрать сдвиг \tau_i меньший младшего собственного значения T_i.
- Вычислить разложение Холецкого T_i-\tau^2_iI=B_i^TB_i, где B_i - верхняя треугольная матрица с положительной диагональю.
- T_{i+1}=B_iB_i^T+\tau_i^2I.
Отметим, что два шага LR-итерации с нулевым сдвигом эквивалентны одному шагу QR-итерации. Итерационная процедура приводит матрицу к диагональному виду, тем самым вычисляя собственные значения исходной матрицы. LR-алгоритм достаточно легко может быть переформулирован с заметными упрощениями для задачи поиска сингулярных значений двухдиагональных матриц. А именно, будем вычислять последовательность двухдиагональных матриц B_i без непосредственного вычисления T_i(которые в данном случае будут трехдиагональными). Пусть матрица B_i имеет диагональные элементы a_1 \ldots a_n и наддиагональные элементы b_1 \ldots b_{n-1}, а матрица B_{i+1} - диагональные элементы \widehat{a}_1 \ldots \widehat{a}_n и наддиагональные элементы \widehat{b}_1 \ldots \widehat{b}_{n-1}. Тогда шаг LR-итерации в терминах матриц B_i можно привести к простому циклу, пробегающему значения j от 1 до n-1:
- \widehat{a}^2_j = a^2_j+b^2_j-\widehat{b}^2_{j-1}-\delta
- \widehat{b}^2_j = b^2_j\dot (a^2_{j+1}/a^2_j)
и вычислению \widehat{a}^2_n = a^2_n-\widehat{b}^2_{n-1}-\delta. Очевидно, что работу с извлечением квадратных корней выгодно вести лишь после окончания работы алгоритма, поэтому можно ввести замену q_j=a^2_j,\; e_j=b^2, что в итоге приводит к так называемому алгоритму qds. Формулы алгоритма следующие:
- \widehat{q}_j = q_j + e_j - \widehat{e}_{j-1} - \delta, \quad j \in [1,n-1]
- \widehat{e}_j = e_j \cdot q_{j+1} / \widehat{q}_j, \quad j \in [1,n-1]
- \widehat{q}_n = q_n - \widehat{e}_{n-1} - \delta.
Здесь q_j, \; j \in [1,n] и e_j, \; j \in [1,n-1] - квадраты элементов главной и верхней побочной диагонали соответственно. Крышка означает выходные переменные, а
\delta - сдвиг (параметр алгоритма). Такая математическая запись наиболее компактна и соответствует так называемой qds-итерации.
1.2.2 Математическое описание итерации алгоритма dqds
Представим теперь математическую запись, приближенную к dqds-итерации (с математической точки зрения qds и dqds-итерации эквивалентны) с введенными вспомогательными переменными
t_j и d_j. Итерация алгоритма dqds преобразует входную двухдиагональную матрицу B в выходную \widehat{B}.
Входные и выходные данные: q_{j}, \; j\in [1,n], \; e_{k}, \; k\in [1,n-1] - квадраты элементов главной и побочной диагонали входной матрицы B, \widehat{q}_j , \; \widehat{e}_k - то же для вычисляемой матрицы \widehat{B}..
Формулы метода выглядят следующим образом:
- d_1 = q_1 - \delta, \; q_n = d_n
- для \quad j\in [1,n-1]:
- \widehat{q}_j = d_j + e_j
- t_j = q_{j+1}/\widehat{q}_j
- \widehat{e}_j=e_j \cdot t_j
- d_{j+1} = d \cdot t - \delta
1.3 Вычислительное ядро алгоритма
Вычислительным ядром алгоритма является последовательный расчёт квадратов диагональных (\widehat{q}_j) и внедиагональных (\widehat{e}_k) элементов выходной матрицы. Учитывая использование вспомогательных переменных расчёт каждой новой пары содержит по одной операции сложения, вычитания и деления, а также две операции умножения.
1.4 Макроструктура алгоритма
Алгоритм состоит из отдельного вычисления начального значения вспомогательной переменной d, последующего (n-1)-кратного выполнения повторяющейся последовательности из 5 операций (+,/,*,*,-) для вычисления квадратов диагональных (\widehat{q}_j) и внедиагональных (\widehat{e}_k) элементов выходной матрицы и завершающего вычисления крайнего значения \widehat{q}_n.
1.5 Схема реализации последовательного алгоритма
Отметим, что выходные данные сразу могут быть записаны на место входных (это учтено в схеме), также для хранения вспомогательных переменных t_j и d_j достаточно двух перезаписываемых переменных. Таким образом элементы главной (q_j) и побочной (e_k) диагонали входной матрицы последовательно перезаписываются соответствующими элементами выходной матрицы.
Последовательность исполнения метода следующая:
1. Вычисляется начальное значение вспомогательной переменной d = q_1-\delta.
2. Производится цикл по j от 1 до n-1, состоящий из:
- 2.1 Вычисляется значение q_j = d + e_j;
- 2.2 Вычисляется значение вспомогательной переменной t = q_{j+1}/q_j;
- 2.3 Вычисляется значение e_j = e_j \cdot t;
- 2.4 Вычисляется значение вспомогательной переменной d = d \cdot t - \delta.
3. Вычисляется q_n = d.
Легко заметить, что можно представить вычисления в другой форме, например, в виде qds-итерации (см. Математическое описание dqds-итерации), однако, именно dqds реализация вычисления позволяет достичь высокой точности[1].
1.6 Последовательная сложность алгоритма
Для выполнения одной итерации dqds необходимо выполнить:
- n-1 делений,
- 2n-2 умножений,
- 2n-1 сложений/вычитаний.
Таким образом одна dqds-итерация имеет линейную сложность.
1.7 Информационный граф
1.8 Ресурс параллелизма алгоритма
Как видно из информационного графа алгоритма, на каждом шаге основного цикла возможно лишь параллельное выполнение операции умножения (2.2) и умножения+сложения (2.4). Это позволяет сократить число ярусов на одной итерации цикла c 5 до 4, а общее число ярусов алгоритма с 5n-4 до 4n-3. Ярусы с операциями умножения состоят из двух операций, остальные же из одной.
1.9 Входные и выходные данные алгоритма
Входные данные: Квадраты элементов основной и верхней побочной диагонали двухдиагональной матрицы (вектора q длины n и e длины n-1), а также параметр сдвига \delta.
Объём входных данных: 2n.
Выходные данные: Квадраты элементов основной и верхней побочной диагонали выходной двухдиагональной матрицы.
Объём выходных данных: 2n-1.
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности при наличии возможности параллельного выполнения операций умножения составляет \frac{5n-4}{4n-3}, т.е. алгоритм плохо распараллеливается.
Вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных - константа.
Описываемый алгоритм является полностью детерминированным.
2 Программная реализация алгоритмов
2.1 Особенности реализации последовательного алгоритма
Алгоритм на языке Matlab может быть записан так:
d = q(1)-delta;
for j = 1:n-1
q(j)=d+e(j);
t=q(j+1)/q(j);
e(j) = e(j)*t;
d = d*t-delta;
end
q(n) = d;
Как говорилось в cхеме реализации последовательного алгоритма, вычисляемые данные записываются сразу на место входных.
2.2 Возможные способы и особенности параллельной реализации алгоритма
Итерация dqds практически полностью последовательна. Единственная возможность - одновременное выполнение операции умножения (2.3) и операции (2.4) умножения и сложения, что дает небольшой выигрыш в производительности.
Сам алгоритм dqds реализован в функции xBDSQR пакета LAPACK и используется при её вызове без расчёта сингулярных векторов.
2.3 Результаты прогонов
2.4 Выводы для классов архитектур
Эффективное выполнение алгоритма возможно только на вычислительных устройствах с одним или двумя ядрами.
3 Литература
- ↑ Перейти обратно: 1,0 1,1 1,2 Деммель Д. Вычислительная линейная алгебра. – М : Мир, 2001.
- ↑ Hogben L. (ed.). Handbook of linear algebra. – CRC Press, 2006.
- ↑ Fernando K. V., Parlett B. N. Accurate singular values and differential qd algorithms //Numerische Mathematik. – 1994. – Т. 67. – №. 2. – С. 191-229.
- ↑ Parlett B. N., Marques O. A. An implementation of the dqds algorithm (positive case) //Linear Algebra and its Applications. – 2000. – Т. 309. – №. 1. – С. 217-259.
- ↑ Aishima K. et al. On convergence of the DQDS algorithm for singular value computation //SIAM Journal on Matrix Analysis and Applications. – 2008. – Т. 30. – №. 2. – С. 522-537.