Участник:Liebeann/Принадлежность точки многоугольнику

Автор статьи: Липкина Анна

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

На плоскости дан произвольный многоугольник с [math]N[/math] вершинами и точка [math]X[/math]. Требуется определить положение точки относительно многоугольника: находится ли точка внутри многоугольника, на его границе, совпадает с вершиной или находится вне многоугольника.

1.2 Математическое описание алгоритма

Дано: Многоугольник [math]P[/math]с [math]N[/math] вершинами и точка [math]X[/math]. Каждая вершина многоугольника и точка [math]X[/math] описываются парой координат [math](x, y)[/math].

Обозначения:

• [math]int(P)[/math] — множество строго внутренних точек многоугольника [math]P[/math];
• [math]V(P) = \{v_0, v_2, \dots, v_{N - 1} \}[/math] — упорядоченноый набор точек, являющихся вершинами многоугольника [math]P[/math];
• [math]D(P)[/math] — множество граничных точек многоугольника [math]P[/math], без учета вершин многоугольника;
• [math]out(P)[/math] — множество строго внешних по отношению к [math]P[/math] точек;
• [math]\delta_{\varepsilon}(X)[/math] — [math]\varepsilon[/math]-окрестность точки [math]X[/math], или это следующее множество точек: [math]\{x \in \mathbb{R}^2 | \rho(x, X) \leqslant \varepsilon \}[/math], где [math]\rho(A, B) = \sqrt{(A_x - B_x)^2 + (A_y - B_y) ^ 2}[/math] — Евклидово расстояние между точками [math]A[/math] и [math]B[/math], а [math]A = (A_x, A_y)[/math] — точка, задающаяся своими координатами по осям.

Выход: вывести:

• 1, если [math]X \in int(P)[/math]
• 2, если [math]X \in V(P)[/math]
• 0, если [math]X \in D(P)[/math]
• -1, если [math]X \in out(P)[/math]

Алгоритм:

1) Сначала проверим, принадлежит ли [math]X[/math] множеству [math]V(P)[/math]. Для этого достаточно перебрать все вершины [math]V(P)[/math] и для каждой проверить, лежит ли [math]X[/math] в маленькой [math]\varepsilon[/math]-окрестности текущей вершины многоугольника. Более формально:

для всех v принадлежащих V(P):
   если X принадлежит епсилон-окрестности v:
        вернуть 2

2) Если точка не совпадает ни с одной вершиной, то проверим, принадлежит ли [math]X[/math] множеству [math]D(P)[/math]. Для этого переберем все ребра многоугольника [math](v_i, v_{i + 1})[/math] и посчитаем следующие величины:

Пусть [math]v_i^l = v_i - X, v_i^r = v_{(i + 1) \% N} - X[/math]

[math]s_i = \langle v_i^l, v_i^r \rangle [/math] — скалярное произведение векторов [math]v_i^l, v_i^r[/math]

[math]t_i = v_i^l \times v_i^r[/math] — модуль вектора, полученного векторным произведением векторов [math]v_i^l, v_i^r[/math]

Теоретически, точка лежит на ребре (строго, не совпадает ни с одной из вершин ребер), если [math]s_i \lt 0[/math] и [math]d_i = 0[/math].

Практически, равенство нулю нужно превратить в [math]|d_i| \leqslant \varepsilon [/math].

Если все условия выполнены, то возвращаем 0.

3) Если [math]X \notin V(P)[/math] и [math]X \notin D(P)[/math]:

Посчитаем следующую сумму ориентированных углов:

[math]S = \sum_{i=0}^{N - 1} angle (v_i - X, v_{(i + 1) \% N} - X)[/math]

где [math]angle(a, b)[/math] — ориентированный угол между векторами [math]a[/math] и [math]b[/math].

Есть следующие два варианта:

• [math]|S| \lt \varepsilon \Rightarrow X \in out(P) [/math]
• [math]|S| \in \delta_{\varepsilon}(2 \pi) \Rightarrow X \in int(P)[/math]

Замечание: здесь вводятся [math]\varepsilon[/math] - окрестности из-за того, что работа происходит с вещественными числами.

1.3 Вычислительное ядро алгоритма

Как нетрудно видеть, сложность выполнения каждого из шагов 1) – 3) равна [math]O(N)[/math]. Но в данной задаче есть один нюанс — сложность чтения данных составляет также [math]O(N)[/math]. Причем, скорость чтения данных с диска гораздо медленее, чем оперирование с данными в процессе выполненения программы, поэтому, если говорить честно, то основная сложность алгоритма приходится именно на чтение данных (что впоследствии и будет видно на графиках сильной масштабируемости). Но проблема в том, что чтение с диска достаточно плохо параллелится (с точки зрения времени чтения), то есть является "узким местом" алгоритма. Назовем фактическим вычислительным ядром алгоритма именно чтение входных данных.

Поэтому, будем считать, что данные уже лежат в памяти программы (то есть чтение данных не вносит значительный вклад в время работы алгоритма) (такое запросто может быть, так как выбранный алгоритм спокойно может быть подзадачей какой-то программы), и тогда, основная сложность алгоритма придется на шаги 1) – 3). Формальным вычислительным ядром, или вычислительным ядром алгоритма назовем именно эти шаги. Формально, я продолжу писать, что данные считываются из памяти.

1.4 Макроструктура алгоритма

0) Чтение входных данных: точка [math]X[/math] и многоугольник [math]P[/math];

1) Проверка принадлежности [math]X[/math] набору [math]V(P)[/math];

2) Проверка принадлежности [math]X[/math] множеству [math]D(P)[/math];

3) Проверка принадлежности [math]X[/math] множеству [math]int(P)[/math].

1.5 Схема реализации последовательного алгоритма

Псевдокод алгоритма:

# Ввод данных
X = input_point()
P = input_polygon()

if is_one_of_vertex(X, P): # Если точка X является одной из вершин многоугольника
   print(2)
else if is_one_of_edge(X, P): # Если точка X лежит на одном из ребер многоульника
   print(0)
else if is_inside(X, P): # Если точка X строго внутри многоугольника
   print(1)
else: # Если точка X строго снаружи многоугольника
   print(-1) 

1.6 Последовательная сложность алгоритма

В силу описания предложенного алгоритма с разделе на п.1.2, время работы всего алгоритма линейное от количества вершин многоульника [math]P[/math], то есть([math]O(N)[/math] операций) (под операциями здесь подразумеваются сложения и умножения чисел).

1.8 Ресурс параллелизма алгоритма

Как нетрудно видеть, вычислительное ядро алгоритма легко параллелится: достаточно каждому процессу [math]p_i[/math] дать свой "кусок" (ломанную последовательных вершин многоугольника) [math]P_{p_i}[/math] так, чтобы в объединении эти ломанные давали весь многоугольник, а сами ломанные могут пересекаться только по вершине. Далее посчитаем для каждого процесса следующие величины:

1) [math]\text{vertex_flag}_{p_i}[/math] — принадлежность точки [math]X[/math] одной из вершин [math]P_{p_i}[/math];

2) [math]\text{edge_flag}_{p_i}[/math] — принадлежность точки [math]X[/math] одному из ребер [math]P_{p_i}[/math];

3) [math]\text{angle_sum}_{p_i}[/math] — сумма ориентированных углов, описанная в на п.1.2 в применении к [math]P_{p_i}[/math] (естественно, без замыкания этой ломанной по первой вершине).

Теперь, чтобы получить исходный ответ, посчитаем следующие величины:

1) [math]\text{vertex_flag} = \bigvee \limits_{p_i} \text{vertex_flag}_{p_i}[/math], [math]\bigvee[/math] — логическое ИЛИ;

2) [math]\text{edge_flag} = \bigvee \limits_{p_i} \text{edge_flag}_{p_i}[/math];

3) [math]\text{angle_sum} = \sum \limits_{p_i} \text{angle_sum}_{p_i}[/math];

На основе этих величин, очевидно, делается вывод о расположении точки [math]X[/math] относительно многоугольника [math]P[/math].

Так как оптимальнее всего распределить данные между процессами равномерно, то будем считать, что каждому процессу приходит примерно [math]\left[\dfrac{N}{K}\right][/math] последовательных вершин, где [math]K[/math] — количество процессов.

Тогда сложность алгоритма составит: [math]O\left(\left[\dfrac{N}{K}\right]\right) + O(K)[/math]

Первое слагаемое — параллельный подсчет величин [math]\text{vertex_flag}_{p_i}, \text{edge_flag}_{p_i}, \text{angle_sum}_{p_i}[/math] каждым процессом [math]p_i[/math].

Второе слагаемое — получение из этих величин посредством логического или алгебраического суммирования величин [math]\text{vertex_flag}, \text{edge_flag}, \text{angle_sum}[/math].

Если [math]K^2 \lt N[/math], то основной вклад в сумму будет вносить член [math]O\left(\left[\dfrac{N}{K}\right]\right)[/math].

Иначе, итоговая сложность будет равна [math]O(K)[/math].

Минимальная асимптотическая сложность, как нетрудно видеть, будет достигаться при [math]K = \sqrt{N}[/math] и составит [math]\sqrt{N}[/math].

1.9 Входные и выходные данные алгоритма

На вход программе подаются:

1) N — число вершин в многоугольнике [math]P[/math]; [math]N \geqslant 3[/math]

2) Точка [math]X[/math], описываемая парой вещественных чисел [math](X_x, X_y)[/math]

3) Набор из [math]N[/math] точек, последовательно перечисленных в каком-либо порядке обхода многоугольника [math]P[/math]. Каждая точка [math]v_i[/math] описывается парой вещественных чисел [math](v_{i, x}, v_{i, y})[/math]

На выходе программы ожидается число, характеризующее позицию точки [math]X[/math] относительно многоугольника [math]P[/math]:

• 1, если [math]X \in int(P)[/math]
• 2, если [math]X \in V(P)[/math]
• 0, если [math]X \in D(P)[/math]
• -1, если [math]X \in out(P)[/math]

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета.

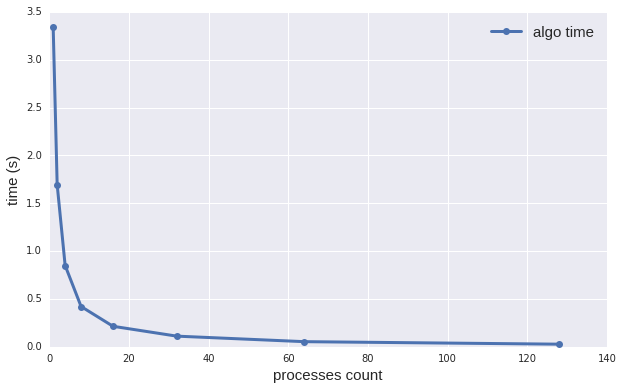
Сначала приведем график сильной масштабируемости для формального вычислительного ядра алгоритма:

В качестве входных данных был сгенерирован правильный [math]10^8[/math]-угольник с центроидом в начале координат и радиусом 15 (радиус правильного многоугольника — расстояние от его центроида до любой вершины), а точка [math]X = (0, 0)[/math].

Количество рассматриваемых процессов: [math]\{1, 2, 4, 8, 16, 32, 64, 128\}[/math]

Как нетрудно видеть, время выполнения алгоритма уменьшается с ростом количества процессов, то есть выигрыш есть. Но с ростом количества процессов этот выигрыш все меньше из-за раскладных расходов на распараллеливание алгоритма.

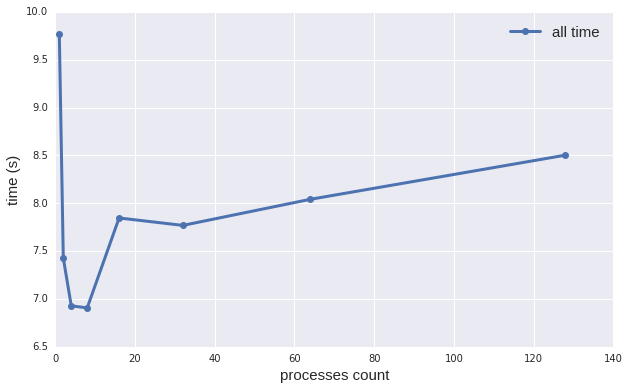
Теперь рассмотрим зависимость времени выполнения программы с учетом чтения входных данных (то есть фактическое вычислительное ядро) от количества процессов:

Как и ожидалось, общее время выполнения программы гораздо больше, чем время выполнения алгоритма. Причем, как видно из графика, время выполнения примерно одинаковое для всех процессов. Флуктуации во времени выполнения связаны с кешированием входных данных или его отсутствием.

2.7 Существующие реализации алгоритма

Последовательные реализации:

• http://www.e-maxx-ru.1gb.ru/algo/pt_in_polygon
• https://github.com/BorysMinaiev/cg/blob/master/include/cg/algo/point_inside_polygon.h
• https://github.com/rubenv/point-in-svg-polygon

Параллельные реализации:

Не обнаружено

3 Литература

• http://ru-wiki.org/wiki/Задача_о_принадлежности_точки_многоугольнику
• http://neerc.ifmo.ru/wiki/index.php?title=Принадлежность_точки_выпуклому_и_невыпуклому_многоугольникам
• https://habrahabr.ru/post/301102/