Участник:Abogovski/Вспомогательная задача при решении задачи Штурма-Лиувилля с условиями сопряжения

Боговский Антон, 409

1 Свойства и структура алгоритмов

К этой вспомогательной задаче (см. Математическое описание алгоритма) сводится решение задачи Штурма-Лиувилля с условия сопряжения, возникающей при разделении переменных в краевой задаче для эллиптического оператора с кусочно-постоянными коэффицентами. Ищутся области (углы) для которых, существуют собственное число равное единице.

1.1 Общее описание алгоритма

Искомые области находятся перебором параметров области (углы, на которых коэффицент постоянен, и значения коэффицента на этих подобластях.

1.2 Математическое описание алгоритма

Рассмотрим задачу Дирихле на ограниченной области для эллиптического уравнения в дивергентной форме с кусочно-постоянными коэффицентами. [math]div(\varkappa grad u) = div F [/math], где коэффицент [math]\varkappa[/math] -- кусочно-постоянный. При решении задачи методом разделения переменных в полярных возникает задача Штурма-Лиувилля относительного полярного угла [math]\Phi'(\varphi) = \lambda \Phi(\varphi)[/math] c условиями сопряжения на разрывах коэффицента: непрерывность [math]\Phi(\varphi)[/math] и [math]\varkappa(\varphi)\Phi'(\varphi)[/math].

В качестве области для модельной задачи возьмем круг (или сектор круга) с радиальными линиями разрыва [math]\varkappa(\varphi)[/math]. Тогда на каждом отрезке непрерывности [math]\varkappa(\varphi)[/math] решение -- линейная комбинация [math]cos(\sqrt{-\lambda}\varphi)[/math] и [math]sin(\sqrt{-\lambda}\varphi)[/math]. Если для области такого вида (набора значений [math]\varkappa[/math] и величин углов) существуют набор постоянных при [math]cos(\sqrt{-\lambda}\varphi)[/math] и [math]sin(\sqrt{-\lambda}\varphi)[/math], такой что граничные условия и условия сопряжения выполнены, то существует собственная функция.

Ищем такие области. Заметим, что решения задачи штурма Лиувилля зависят от [math]\alpha = \sqrt{-\lambda}\varphi[/math] -- перейдем к такой переменной. Зададим граничное условие на одной стороне сектора, условия сопряжения на линиях разрыва и проверим (переберем) различные значения [math]\alpha, \varkappa[/math] на выполнение граничного условия на правой стороне.

(Условия сопряжения дают связь между коэффицентами при [math]cos,sin[/math] через композицию матриц растяжения и поворота, зависящих от [math]\alpha, \varkappa[/math]).

1.3 Вычислительное ядро алгоритма

Перебор параметров. Можно рассматривать вычислительное как обход дерева всех наборов значений параметров.

• Для первой подобласти фиксируется значение [math]\varkappa=1[/math] и поддиапазон перебора значений [math]\alpha[/math]
• Остальные значения перебираются в заданном диапазоне -- обход дерева всех наборов значений параметра (при заданном шаге по значениям).

1.4 Макроструктура алгоритма

• Для каждого процесса из его номера вычисляется поддерево наборов значений для обхода.
• Каждым из процессов выполняется обход своего поддерева
• 0-ой процесс, закончив обход своего поддерева, собирает все результаты и сохраняет их в файл с уникальным именем

1.5 Схема реализации последовательного алгоритма

В первой подобласти: зафиксируем [math]\varkappa=1[/math] Далее перебор значений остальных параметров.

1.6 Последовательная сложность алгоритма

n = ЧИСЛО_ЛИНИЙ_РАЗРЫВА k = ЧИСЛО_ЗНАЧЕНИЙ_В_ДИАПОЗОНЕ_ПЕРЕБОРА

СЛОЖНОСТЬ = [math]O(k^{2n})[/math]

1.7 Информационный граф

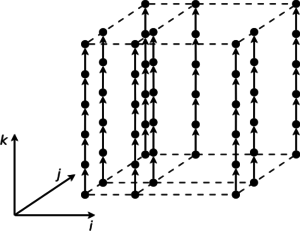
Это очень важный раздел описания. Именно здесь можно показать (увидеть) как устроена параллельная структура алгоритма, для чего приводится описание и изображение его информационного графа (графа алгоритма ). Для рисунков с изображением графа будут составлены рекомендации по их формированию, чтобы все информационные графы, внесенные в энциклопедию, можно было бы воспринимать и интерпретировать одинаково. Дополнительно можно привести полное параметрическое описание графа в терминах покрывающих функций .

Интересных вариантов для отражения информационной структуры алгоритмов много. Для каких-то алгоритмов нужно показать максимально подробную структуру, а иногда важнее макроструктура. Много информации несут разного рода проекции информационного графа, выделяя его регулярные составляющие и одновременно скрывая несущественные детали. Иногда оказывается полезным показать последовательность в изменении графа при изменении значений внешних переменных (например, размеров матриц): мы часто ожидаем "подобное" изменение информационного графа, но это изменение не всегда очевидно на практике.

В целом, задача изображения графа алгоритма весьма нетривиальна. Начнем с того, что это потенциально бесконечный граф, число вершин и дуг которого определяется значениями внешних переменных, а они могут быть весьма и весьма велики. В такой ситуации, как правило, спасают упомянутые выше соображения подобия, делающие графы для разных значений внешних переменных "похожими": почти всегда достаточно привести лишь один граф небольшого размера, добавив, что графы для остальных значений будут устроены "точно также". На практике, увы, не всегда все так просто, и здесь нужно быть аккуратным.

Далее, граф алгоритма - это потенциально многомерный объект. Наиболее естественная система координат для размещения вершин и дуг информационного графа опирается на структуру вложенности циклов в реализации алгоритма. Если глубина вложенности циклов не превышает трех, то и граф размещается в привычном трехмерном пространстве, однако для более сложных циклических конструкций с глубиной вложенности 4 и больше необходимы специальные методы представления и изображения графов.

В данном разделе AlgoWiki могут использоваться многие интересные возможности, которые еще подлежат обсуждению: возможность повернуть граф при его отображении на экране компьютера для выбора наиболее удобного угла обзора, разметка вершин по типу соответствующим им операций, отражение ярусно-параллельной формы графа и другие. Но в любом случае нужно не забывать главную задачу данного раздела - показать информационную структуру алгоритма так, чтобы стали понятны все его ключевые особенности, особенности параллельной структуры, особенности множеств дуг, участки регулярности и, напротив, участки с недерминированной структурой, зависящей от входных данных.

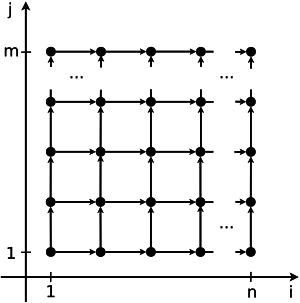
На рис.1 показана информационная структура алгоритма умножения матриц, на рис.2 - информационная структура одного из вариантов алгоритма решения систем линейных алгебраических уравнений с блочно-двухдиагональной матрицей.

Рис.1. Информационная структура алгоритма умножения матриц

Рис.2. Информационная структура одного из вариантов алгоритма решения систем линейных алгебраических уравнений с блочно-двухдиагональной матрицей

1.8 Ресурс параллелизма алгоритма

Так как структура алгоритма представляет собой дерево (с большим количеством потомков в каждом узле) -- алгоритм хорошо распараллеливается. Наблюдается линейная масштабируемость. Сбор и сохранение данных в конце почти не влиют на производительность.

1.9 Входные и выходные данные алгоритма

Параметрами задачи являются: число областей непрерывности, диапазон и точность перебора [math]\varkappa, \alpha[/math], требуемая точность выполнения граничного условия. Выходные данные: наборы [math]\varkappa, \alpha[/math] -- с их помощью можно построить искомые области.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Ключевым ограничением масштабируемости является сбор результатов одним процессом.

2.6 Выводы для классов архитектур

• Алгоритм имеет линейную масштабируемость на любой системе, где сохранение данных не займет существенную часть времени. (вычислительные ядра не взаимодействуют)
• Алгоритм не учитывает возможность оптимизации с помощью векторизации.