Участник:Maria Zaitseva/PAM (Partitioning Around Medoids): различия между версиями
Kovalexal (обсуждение | вклад) |
ASA (обсуждение | вклад) |
||
| (не показано 40 промежуточных версий 5 участников) | |||
| Строка 1: | Строка 1: | ||
| + | {{Assignment|ASA|Dexter}} | ||
| + | |||
| + | {{algorithm | ||
| + | | name = Partitioning Around Medoids | ||
| + | | serial_complexity = <math>O(Tkn^2)</math> | ||
| + | | input_data = <math>\frac{n (n - 1)}{2}</math> | ||
| + | | output_data = <math>k</math> | ||
| + | | pf_height = <math>O(Tkn)</math> | ||
| + | | pf_width = <math>O(k(n-k))</math> | ||
| + | }} | ||
| + | |||
| + | |||
| + | |||
Авторы: [[Участник: Maria Zaitseva|Зайцева М.Ф.]], [[Участник: kovalexal|Ковальчук А.А.]]. | Авторы: [[Участник: Maria Zaitseva|Зайцева М.Ф.]], [[Участник: kovalexal|Ковальчук А.А.]]. | ||
| − | '''PAM (Partitioning Around Medoids)''' | + | Авторы работали над каждым разделом статьи совместно (совместно искали и изучали материалы, формулировали описание и заполняли описание статьи на сайте). За содержание каждого из пунктов отвечают оба автора. |
| + | |||
| + | '''PAM (Partitioning Around Medoids)''' – алгоритм разбиения множества объектов на [https://ru.wikipedia.org/wiki/Кластер кластеры], базирующийся на использовании наиболее представительных объектов каждого кластера ([https://ru.wikipedia.org/wiki/Медоид медоидов]) для их описания. Был разработан в 1987 году Леонардом Кауфманом и Питером Русивом <ref>Kaufman L., Rousseeuw P. J. Finding groups in data: an introduction to cluster analysis. – John Wiley & Sons, 2009. – Т. 344.</ref>. Показывает хорошие результаты разбиения на небольших наборах данных, однако имеет высокую вычислительную сложность, ввиду чего неэффективно работает на больших наборах данных. | ||
= Свойства и структура алгоритма = | = Свойства и структура алгоритма = | ||
== Общее описание алгоритма == | == Общее описание алгоритма == | ||
| − | Данный алгоритм используется для решения задачи [https://ru.wikipedia.org/wiki/Кластерный_анализ кластеризации] множества объектов на заранее известное число кластеров <math>k</math>. Каждый кластер характеризуется наиболее представительным (центральным ) объектом | + | Данный алгоритм используется для решения задачи [https://ru.wikipedia.org/wiki/Кластерный_анализ кластеризации] множества объектов на заранее известное число кластеров <math>k</math>. Каждый кластер характеризуется наиболее представительным (центральным ) объектом – медоидом. Принадлежность объекта к соответствующему кластеру определяется индексом наиболее близкого к нему медоида. |
На вход алгоритму может подаваться набор объектов с заданной функцией расчета дистанции между ними, либо матрица расстояний, характеризующая дистанции между каждой парой объектов, а также число кластеров, на которое необходимо разбить множество объектов. На выходе алгоритм выдает множество объектов, принятых в качестве медоидов. | На вход алгоритму может подаваться набор объектов с заданной функцией расчета дистанции между ними, либо матрица расстояний, характеризующая дистанции между каждой парой объектов, а также число кластеров, на которое необходимо разбить множество объектов. На выходе алгоритм выдает множество объектов, принятых в качестве медоидов. | ||
| Строка 34: | Строка 49: | ||
''Выходные данные'': | ''Выходные данные'': | ||
| − | * <math>m = \{m_1,\dots,m_k\}\subset o</math> –– множество индексов объектов, принятых в качестве медоидов | + | * <math>m = \{m_1,\dots,m_k\}\subset o</math> –– множество индексов объектов, принятых в качестве медоидов; <math> M </math>--множество медоидов. |
Принадлежность объекта к определенному кластеру определяется как индекс ближайшего к нему медоида: | Принадлежность объекта к определенному кластеру определяется как индекс ближайшего к нему медоида: | ||
| Строка 40: | Строка 55: | ||
Основная задача состоит в выборе такого множества индексов медоидов <math>m</math>, наилучшим образом минимизирующего функционал: | Основная задача состоит в выборе такого множества индексов медоидов <math>m</math>, наилучшим образом минимизирующего функционал: | ||
| − | :<math>F_o(m) = \sum_{j \in o} d_{jg_m(j)}</math>. | + | :<math>F_o(m) = \sum_{j \in o \backslash m} d_{jg_m(j)}</math>. |
Введем обозначения: | Введем обозначения: | ||
| Строка 84: | Строка 99: | ||
== Макроструктура алгоритма == | == Макроструктура алгоритма == | ||
| − | |||
| − | + | 1. Макрооперация "Выбор следующего медоида" | |
| − | + | :<math>m = m \cup \{ \arg \max_{i \in o \backslash m} \sum_{j \in o \backslash \{m \cup i\} } \max (D_j - d_{ji}, 0) \}</math> | |
| + | |||
| + | 2. Макрооперация "Вычисление стоимости смены текущей конфигурации" | ||
| + | :<math>T_m(i, h) = \sum_{j \in o \backslash \{m \cup h\}} C_{jih}</math> | ||
| + | |||
| + | Таким образом, алгоритм, в терминах макроопераций выглядит следующим образом: | ||
| + | |||
| + | 1. Фаза ''BUILD'' | ||
| + | |||
| + | На данном шаге осуществляется выбор первого медоида. Далее осуществляется макрооперация "Выбор следующего медоида" <math>(k - 1)</math> раз. | ||
| + | |||
| + | 2. Фаза ''SWAP'' | ||
| + | |||
| + | На данном шаге для всех возможных комбинаций медоид-немедоид осуществляется макрооперация "Вычисление стоимости смены текущей конфигурации". Данная операция производится <math>k(n-k)</math> раз для каждой итерации. Среди всех комбинаций выбирается та замена, стоимость которой максимальна. | ||
| + | |||
| + | 3. ''Критерий останова'' | ||
| + | |||
| + | :<math>T_m(i, h) < 0</math> | ||
== Схема реализации последовательного алгоритма == | == Схема реализации последовательного алгоритма == | ||
| Строка 93: | Строка 124: | ||
''Псевдокод алгоритма'': | ''Псевдокод алгоритма'': | ||
| − | '''Вход''': | + | '''Вход''': Объем входных данных: <math>n\times n + 2</math>. Матрица дистанций D (<math>n\times n</math> вещественных чисел); количество кластеров <math>k \in \mathbb{Z}</math>; максимальное количество итераций алгоритма <math>maxIter \in \mathbb{Z}</math> |
| − | '''Выход''': | + | '''Выход''': Объем выходных данных: <math>k</math>. Множество индексов медоидов <math>m = \{m_1, \dots, m_k\} \subset \mathbb{Z}</math> |
1 # Фаза BUILD | 1 # Фаза BUILD | ||
2 Выбор стартового объекта в качестве начального медоида: m = {первый медоид} | 2 Выбор стартового объекта в качестве начального медоида: m = {первый медоид} | ||
| Строка 114: | Строка 145: | ||
18 Иначе: | 18 Иначе: | ||
19 m = m + {h} - {i} | 19 m = m + {h} - {i} | ||
| + | |||
| + | На фазе ''BUILD'' осуществляется построение начального множества медоидов. Данный процесс производится итерационно до тех пор, пока не будет найдено необходимое число медоидов. | ||
| + | На фазе ''SWAP'' производится попытка улучшить множество выбранных медоидов. Данный процесс также производится итерационно то тех пор, пока целевая функция не перестанет улучшаться. Также, для данного шага можно ввести ограничение по числу производимых алгоритмом итераций. | ||
== Последовательная сложность алгоритма == | == Последовательная сложность алгоритма == | ||
| Строка 120: | Строка 154: | ||
* <math>n^2</math> операций сложения и <math>n</math> операций сравнения для выбора начального медоида; | * <math>n^2</math> операций сложения и <math>n</math> операций сравнения для выбора начального медоида; | ||
| − | * <math>\sum_{l=1}^{k-1} 2(n-l) \cdot (n-l-1)=\frac{ | + | * <math>\sum_{l=1}^{k-1} (2(n-l) \cdot (n-l-1)+(n-l))=\frac{1}{6}(k-1)(4k^2 - 12kn + k + 6n(2n-1))</math> операций сложения, вычитания и сравнения для всех итераций выбора медоидов. |
| − | |||
Таким образом, последовательная сложность шага ''BUILD'' оценивается как <math>O(kn^2)</math>. | Таким образом, последовательная сложность шага ''BUILD'' оценивается как <math>O(kn^2)</math>. | ||
| Строка 134: | Строка 167: | ||
== Информационный граф == | == Информационный граф == | ||
| − | |||
| − | + | === Информационный граф шага BUILD === | |
| + | На рис.1 показана информационная структура шага BUILD алгоритма PAM на некотором шаге. | ||
| − | + | [[file:Pam_build.png|thumb|center|553px|Рис.1. Информационная структура шага BUILD алгоритма PAM на шаге <math>t</math>]] | |
| − | + | ''Операции'': | |
| + | * <math>sum_{o,m_t}(i) = \sum_{j \in o \backslash \{m \cup i\}} \max (D_j, d_{ji})</math> –– оценка конфигурации при внесении <math>i</math> в множество индексов медоидов <math>m</math> с множеством объектов <math>o</math>; | ||
| + | * <math>\arg \max</math> –– индекс объекта, дающего наибольшую оценку конфигурации при его внесении в множество индексов медоидов <math>m</math>; | ||
| + | * <math>update(m)</math> –– операция добавления индекса объекта в множество индексов медоидов <math>m</math>. | ||
| − | + | === Информационный граф шага SWAP === | |
| + | На рис.2 показана информационная структура шага SWAP алгоритма PAM на некотором шаге. | ||
| − | + | [[file:Pam_swap_new.png|thumb|center|553px|Рис.2. Информационная структура шага SWAP алгоритма PAM на шаге <math>t</math>]] | |
| − | + | ''Операции'': | |
| − | + | * <math>T_m(i, h) = \sum_{j \in o \backslash \{m \cup h\}} C_{jih} </math> –– стоимость смены конфигурации при замене немедоида <math>h</math> медоидом <math>i</math> в текущей конфигурации <math>m</math>; | |
| + | * <math>\arg \min</math> –– пара <math>(i, h)</math> (медоид-немедоид), замена которой в текущей конфигурации <math>m</math> дает наименьшую стоимость смены; | ||
| + | * <math>swap</math> –– операция замены медоида <math>i</math> на немедоид <math>h</math> в текущей конфигурации <math>m</math>, если стоимость смены отрицательна. | ||
== Ресурс параллелизма алгоритма == | == Ресурс параллелизма алгоритма == | ||
| Строка 163: | Строка 202: | ||
* <math>k(n-k)</math> последовательных операций сравнения. | * <math>k(n-k)</math> последовательных операций сравнения. | ||
| − | Таким образом, параллельная сложность каждого шага ''SWAP'' оценивается как <math>O(kn | + | Таким образом, параллельная сложность каждого шага ''SWAP'' оценивается как <math>O(kn)</math>. |
| − | Заранее число итераций шага ''SWAP'' неизвестно, поэтому принимаем его равным <math>T</math>. Отсюда, общая | + | Заранее число итераций шага ''SWAP'' неизвестно, поэтому принимаем его равным <math>T</math>. Отсюда, общая параллельная сложность алгоритма PAM оценивается как <math>O(Tkn)</math>. |
| − | |||
| − | + | == Входные и выходные данные алгоритма == | |
| − | + | ''Входные данные'': | |
| + | * Массив <math>V</math> из <math>\frac{n(n-1)}{2}</math> вещественных чисел, определяющий набор дистанций между всеми парами объектов (сжатая матрица дистанций). Симметрическая матрица дистанций <math>D\in \mathbb{R}^{n\times n}</math> восстанавливается из этого массива однозначным образом (для восстановления необходимо знать число объектов <math>n</math>): | ||
| + | :<math>D(i, j)=\left\{\begin{matrix} | ||
| + | V[ni - \frac{i(i + 1)}{2} + (j - i - 1)], & i < j\\ | ||
| + | V[nj - \frac{j(j + 1)}{2} + (i - j - 1)], & i > j \\ | ||
| + | 0, & i = j | ||
| + | \end{matrix}\right.</math> | ||
| − | + | * Целое число кластеров <math>k</math>, на которое необходимо разбить множество объектов. | |
| − | + | ''Выходные данные'': | |
| − | + | * Множество <math>m</math>, состоящее из <math>k</math> индексов объектов, принятых в качестве медоидов. Индекс кластера, которому принадлежит объект с индексом <math>i</math> можно восстановить с использованием функции <math>g_m(i)=\arg \min_{m_j\in m} d_{im_j}</math>. | |
| − | |||
| − | |||
== Свойства алгоритма == | == Свойства алгоритма == | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '' | + | 1. ''Соотношение последовательной и параллельной сложности'' в случае неограниченных ресурсов является ''линейным'' как отношение квадратичной сложности к линейной. |
| − | + | 2. ''Вычислительная мощность'' последовательного алгоритма, как отношение числа операций к суммарному объему входных и выходных данных: <math> O(Tk) </math>. | |
| − | + | 3. Алгоритм является ''устойчивым'', так как все операции в алгоритме не подвержены накоплению ошибки. | |
| − | + | 4. Алгоритм является ''не детерминированным'', так как не детерминирован выбор набора медоидов, на которых достигается наилучшая конфигурация. | |
| − | + | 5. Имеет высокую вычислительную сложность (квадратичную) ввиду необходимости полного перебора, поэтому неэффективно работает на больших наборах данных. | |
| − | + | 6. Позволяет работать с произвольными объектами с заданной мерой рассчета расстояний (различий), не требует хранения всего множества объектов. | |
| − | + | 7. Устойчив к выбросам данных (за счет рассмотрения медоидов). | |
= Программная реализация алгоритма = | = Программная реализация алгоритма = | ||
| Строка 210: | Строка 245: | ||
== Масштабируемость алгоритма и его реализации == | == Масштабируемость алгоритма и его реализации == | ||
| − | |||
| − | + | Для изучения масштабируемости алгоритма была выполнена его [https://gitlab.com/kovalexal/pam-lomonosov реализация] с использованием механизма MPI на языке программирования C++. Данная реализация использует библиотеку [http://www.boost.org Boost] (модуль MPI для удобного взаимодействия C++ и MPI и модуль uBLAS для работы с матрицами). Исследование масштабируемости описанной реализации производилось на суперкомпьютере [https://parallel.ru/cluster/lomonosov.html "Ломоносов"]. Для сборки программы использовался компилятор gcc версии 5.2.0 с опциями "-std=c++11 -O3" совместно с OpenMPI версии 1.8.4. | |
| + | |||
| + | В качестве рассматриваемого при оценке набора данных была произведена их генерация на основе двумерного нормального распределения. Для этого сперва выбиралось некоторое количество точек, которые в дальнейшем выступали в качестве центроидов кластеров. Далее, для каждого полученного кластера осуществлялась генерация равного числа точек. | ||
| + | |||
| + | |||
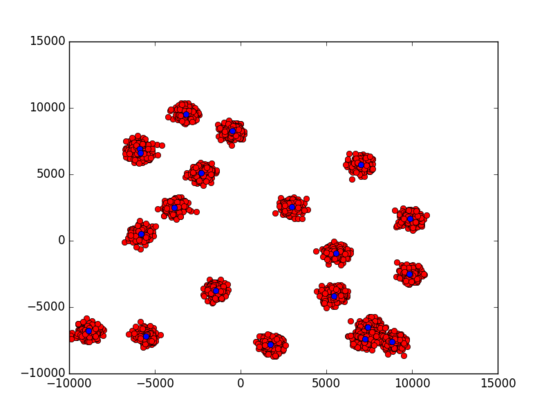
| + | [[file:points.png|thumb|center|553px|Рис.3. Пример сгенерированных данных – 20 кластеров, 5000 точек]] | ||
| + | |||
| + | |||
| + | Набор значений параметров запуска, используемых для оценке масштабируемости представлен ниже: | ||
| + | |||
| + | * Число процессов: [1, 8, 16, 32, 48, 50, 51, 64, 99, 100, 101, 128, 160, 192, 200, 224, 256, 320, 384, 448, 512] | ||
| + | * Число кластеризуемых элементов: от 1000 до 5000 с шагом 250 | ||
| + | * Число кластеров при расчете: 20 | ||
| + | |||
| + | |||
| + | Для оценки производительности алгоритма осуществлялся расчет числа операций с плавающей запятой в секунду (FLOPs или GFLOPs). Для этого при каждом запуске рассчитывалось время работы алгоритма, число итераций шага ''SWAP'', по данным значениям можно получить точное число операций сложения, вычитания и сравнения вещественных чисел (оно равно последовательной сложности алгоритма), поделив его на время работы можно получить оценку числа FLOP в секунду. График изменения производительности в зависимости от числа процессоров и числа кластеризуемых элементов представлен ниже. Интерактивный график доступен по [https://plot.ly/~kovalexal/7/ ссылке]. | ||
| + | |||
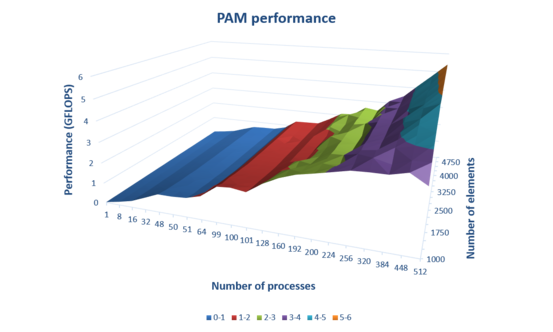
| + | [[file:PAM_perf.png|thumb|center|553px|Рис.4. Изменение производительности в зависимости от числа процессоров и числа кластеризуемых элементов]] | ||
| + | |||
| + | Масштабируемость алгоритма была получена путем деления реальной производительности на пиковую произвдительность <math>s</math> задействованных ядер (пиковая производительность одного ядра "Ломоносова" составляет ''5.686'' GFLOPs). График изменения эффективности в зависимости от числа процессоров и числа кластеризуемых элементов представлен ниже. Интерактивный график доступен по [https://plot.ly/~kovalexal/9/ ссылке]. | ||
| + | |||
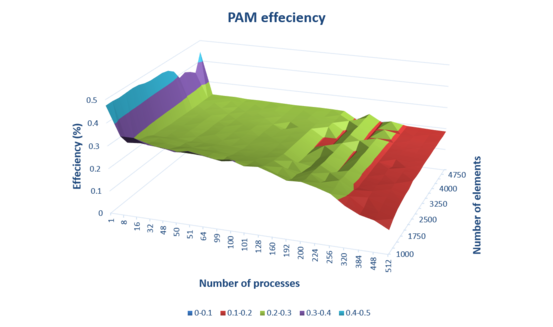
| + | [[file:PAM_eff.png|thumb|center|553px|Рис.5. Изменение эффективности в зависимости от числа процессоров и числа кластеризуемых элементов]] | ||
| − | |||
| − | + | Из полученных значений эффективности можно оценить диапазон эффективности реализации алгоритма: | |
| − | + | ||
| + | * минимальная эффективность: 0.10353% достигается при использовании 512 процессов для кластеризации 1000 элементов на 20 кластеров; | ||
| + | * максимальная эффективность: 0.47637% достигается при использовании 1 процесса для кластеризации 2000 элементов на 20 кластеров. | ||
| + | |||
| + | Построим оценки масштабируемости выбранной реализации алгоритма Partitioning Around Medoids согласно [[Scalability_methodology]]: | ||
| + | |||
| + | * По числу процессов: 6.07542E-04. При увеличении числа процессов эффективность реализации на рассмотренной области значений параметров запуска возрастает, но интенсивность данного роста мала. Для увеличения масштабируемости по числу процессов необходимо увеличить количество операций в секунду, осуществляемых каждым процессом (например, уменьшив время работы алгоритма). Для этого можно применить различные технологии распараллеливания и векторизации вычислений. | ||
| + | * По размеру задачи: 1.91151E-04. При увеличении размера задачи эффективность возрастает, однако данный рост достаточно слаб. Это говорит нам о том, что эффективность алгоритма слабо зависит от размера входной задачи. | ||
| + | * По двум направлениям: 2.03868E-05. При рассмотрении увеличения как размера входа, так и числа процессов на всей рассмотренной области значений эффективность увеличивается, однако скорость увеличения эффективности небольшая. В совокупности с тем фактом, что разница между минимальной и максимальной эффективностью на рассмотренной области параметров небольшая, эффективность с увеличением масштабов возрастает, но медленно. | ||
== Динамические характеристики и эффективность реализации алгоритма == | == Динамические характеристики и эффективность реализации алгоритма == | ||
| Строка 223: | Строка 285: | ||
== Выводы для классов архитектур == | == Выводы для классов архитектур == | ||
| − | + | == Существующие реализации алгоритма == | |
1. Последовательные реализации | 1. Последовательные реализации | ||
| Строка 235: | Строка 297: | ||
* В пакете [https://cran.r-project.org/package=sprint SPRINT] на языке R (Свободное распространение ([https://ru.wikipedia.org/wiki/GNU_General_Public_License#GPL_v1 GPL])) | * В пакете [https://cran.r-project.org/package=sprint SPRINT] на языке R (Свободное распространение ([https://ru.wikipedia.org/wiki/GNU_General_Public_License#GPL_v1 GPL])) | ||
| − | |||
= Литература = | = Литература = | ||
[[en:Description of algorithm properties and structure]] | [[en:Description of algorithm properties and structure]] | ||
Текущая версия на 16:28, 19 декабря 2016
 | Эта работа успешно выполнена Преподавателю: в основное пространство, в подстраницу Данное задание было проверено и зачтено. Проверено Dexter и ASA. |
| Partitioning Around Medoids | |
| Последовательный алгоритм | |
| Последовательная сложность | O(Tkn^2) |
| Объём входных данных | \frac{n (n - 1)}{2} |
| Объём выходных данных | k |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | O(Tkn) |
| Ширина ярусно-параллельной формы | O(k(n-k)) |
Авторы: Зайцева М.Ф., Ковальчук А.А..
Авторы работали над каждым разделом статьи совместно (совместно искали и изучали материалы, формулировали описание и заполняли описание статьи на сайте). За содержание каждого из пунктов отвечают оба автора.
PAM (Partitioning Around Medoids) – алгоритм разбиения множества объектов на кластеры, базирующийся на использовании наиболее представительных объектов каждого кластера (медоидов) для их описания. Был разработан в 1987 году Леонардом Кауфманом и Питером Русивом [1]. Показывает хорошие результаты разбиения на небольших наборах данных, однако имеет высокую вычислительную сложность, ввиду чего неэффективно работает на больших наборах данных.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Данный алгоритм используется для решения задачи кластеризации множества объектов на заранее известное число кластеров k. Каждый кластер характеризуется наиболее представительным (центральным ) объектом – медоидом. Принадлежность объекта к соответствующему кластеру определяется индексом наиболее близкого к нему медоида.
На вход алгоритму может подаваться набор объектов с заданной функцией расчета дистанции между ними, либо матрица расстояний, характеризующая дистанции между каждой парой объектов, а также число кластеров, на которое необходимо разбить множество объектов. На выходе алгоритм выдает множество объектов, принятых в качестве медоидов.
Алгоритм состоит из двух последовательных этапов:
1. Шаг BUILD. Построение начального набора k медоидов путем их последовательного выбора. Первый из них выбирается как объект, сумма дистанций которого до всех других объектов минимальна (центральный объект). Каждый следующий выбирается из оставшихся объектов как лучше всего минимизирующий сумму расстояний от объектов до ближайших к ним медоидов. Выбранный набор медоидов характеризует "конфигурацию" кластеров, для которой может быть вычислена ее стоимость.
2. Шаг SWAP. На данном шаге производится попытка улучшить стоимость текущей конфигурации путем перебора всех возможных замен (медоид-немедоид). Среди рассматриваемых конфигураций ищется наиболее оптимальная. В случае, если данная конфигурация по стоимости лучше текущей, она принимается в качестве текущей и шаг повторяется с начала, иначе алгоритм завершается.
Преимущества данного алгоритма по сравнению с подобными ему:
- В отличие от более популярного алгоритма k-means, PAM позволяет работать с произвольными объектами с заданной мерой рассчета расстояний (различий), не требует хранения всего множества объектов (достаточно знать лишь матрицу дистанций, так как медоиды выбираются из множества объектов), а также более устойчив к выбросам в данных (за счет рассмотрения медоидов вместо центроидов);
- В отличие от традиционного k-medoids на шаге BUILD начальные медоиды выбираются более оптимальным образом по сравнению со случайным выбором. Это позволяет уменьшить количество итераций шага SWAP, тем самым сокращая время работы алгоритма.
Недостатком данного алгоритма является неэффективность при больших наборах данных ввиду необходимости полного перебора.
1.2 Математическое описание алгоритма
Входные данные:
- o = \{1,\dots,n\} \subset \mathbb{Z} –– множество индексов объектов
- O = \{O_1,\dots,O_n\} –– множество объектов
- k \leq n –– количество кластеров для разбиения
- d:O\times O\rightarrow \mathbb{R}^{1} –– метрика расчета расстояний между объектами, d_{ij} = d(O_i,O_j)
- D\in \mathbb{R}^{n\times n} –– симметрическая матрица дистанций объектов, где D=(d_{ij}), i \in o, j \in o
Выходные данные:
- m = \{m_1,\dots,m_k\}\subset o –– множество индексов объектов, принятых в качестве медоидов; M --множество медоидов.
Принадлежность объекта к определенному кластеру определяется как индекс ближайшего к нему медоида:
- g_m(i)=\arg \min_{m_j\in m} d_{im_j}.
Основная задача состоит в выборе такого множества индексов медоидов m, наилучшим образом минимизирующего функционал:
- F_o(m) = \sum_{j \in o \backslash m} d_{jg_m(j)}.
Введем обозначения:
- D_j = d_{jg_m(j)} –– индекс первого по близости к j медоида
- E_j = d_{jg_{m \backslash g_m(j)}(j)} –– индекс второго по близости к j медоида
Решение задачи состоит из следующих шагов:
1. Шаг BUILD
1.1. Выбор первого медоида
- m=\{ \arg \min_{i \in o} \sum_{j \in o} d_{ij} \}
1.2 Последовательный выбор оставшихся медоидов до тех пор, пока [math]\left\vert{m}\right\vert \neq k[/math]
- m = m \cup \{ \arg \max_{i \in o \backslash m} \sum_{j \in o \backslash \{m \cup i\} } \max (D_j - d_{ji}, 0) \}
2. Шаг SWAP
2.1. Производится перебор всех возможных пар медоид-немедоид [math](i, h): i \in m, h \in o \backslash m[/math], для каждой из которых рассчитывается стоимость смены текущей конфигурации [math]T_m(i,h)[/math]. При смене конфигурации множество медоидов изменяется [math]m = m \cup \{h\} \backslash \{i\}[/math].
- T_m(i, h) = \sum_{j \in o \backslash \{m \cup h\}} C_{jih}, где C_{jih} –– вклад объекта j в перестановку медоида i и не медоида h.
При этом [math]C_{jih}[/math] рассчитывается по-разному в зависимости от положения [math]j[/math] относительно [math]i[/math] и [math]h[/math] ([math]j[/math] дальше от [math]i[/math] и от [math]h[/math], чем от своего ближайшего медоида; [math]i[/math] оказался ближайшим медоидом [math]j[/math]; [math]j[/math] оказался дальше от [math]i[/math], но ближе к [math]h[/math], чем к своему медоиду).
- C_{jih} = \left\{\begin{matrix} 0, & d_{ji} \gt D_j, d_{jh} \gt D_j \\ d_{jh} - d_{ji}, & d_{ji} = D_j, d_{jh} \lt E_j \\ E_j - D_j, & d_{ji} = D_j, d_{jh} \geqslant E_j \\ d_{jh} - D_j, & d_{ji} \gt D_j, d_{jh} \lt D_j \end{matrix}\right.
Среди всех пар находится такая пара [math](i_s, h_s)[/math], что [math]T_m(i_s, h_s)[/math] минимально.
2.2 В случае, если [math]T_m(i_s, h_s) \geq 0[/math], смена конфигурации медоидов не производится и решение задачи окончено. Иначе производится смена конфигурации и повторяется шаг 2.1.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма на этапе BUILD состоит последовательного выбора такого объекта из числа немедоидов, добавление которого к множеству медоидов максимизирует следующую функцию:
F_{m} = \max_{i \in o \backslash m} \sum_{j \in o \backslash \{m \cup i\} } \max (D_j - d_{ji}, 0)
С каждой следующей итерацией множество просматриваемых немедоидов уменьшается, таким образом, на i-ом шаге итерации необходимо рассчитывать сумму для n - i немедоидов.
Вычислительное ядро алгоритма на этапе SWAP состоит в расчете функции минимизации стоимости изменения конфигурации T_m(i, h) при замене медоида i на немедоид h в текущей конфигурации для всех возможных (i, h): i \in m, h \in o \backslash m:
T_m(i, h) = \sum_{j \in o \backslash \{m \cup h\}} C_{jih}.
1.4 Макроструктура алгоритма
1. Макрооперация "Выбор следующего медоида"
- m = m \cup \{ \arg \max_{i \in o \backslash m} \sum_{j \in o \backslash \{m \cup i\} } \max (D_j - d_{ji}, 0) \}
2. Макрооперация "Вычисление стоимости смены текущей конфигурации"
- T_m(i, h) = \sum_{j \in o \backslash \{m \cup h\}} C_{jih}
Таким образом, алгоритм, в терминах макроопераций выглядит следующим образом:
1. Фаза BUILD
На данном шаге осуществляется выбор первого медоида. Далее осуществляется макрооперация "Выбор следующего медоида" (k - 1) раз.
2. Фаза SWAP
На данном шаге для всех возможных комбинаций медоид-немедоид осуществляется макрооперация "Вычисление стоимости смены текущей конфигурации". Данная операция производится k(n-k) раз для каждой итерации. Среди всех комбинаций выбирается та замена, стоимость которой максимальна.
3. Критерий останова
- T_m(i, h) \lt 0
1.5 Схема реализации последовательного алгоритма
Псевдокод алгоритма:
Вход: Объем входных данных: [math]n\times n + 2[/math]. Матрица дистанций D ([math]n\times n[/math] вещественных чисел); количество кластеров [math]k \in \mathbb{Z}[/math]; максимальное количество итераций алгоритма [math]maxIter \in \mathbb{Z}[/math] Выход: Объем выходных данных: [math]k[/math]. Множество индексов медоидов [math]m = \{m_1, \dots, m_k\} \subset \mathbb{Z}[/math] 1 # Фаза BUILD 2 Выбор стартового объекта в качестве начального медоида: m = {первый медоид} 3 Пока |m| != k: 4 Выбор следующего медоида i_m 5 Добавление найденного медоида в множество: m = m + {i_m} 6 # Фаза SWAP 7 Пока (maxIter--): 8 Лучшая стоимость замены: Tbest = MAXINT 9 Кандидаты на замену: (i_s, h_s) = (-1, -1) 10 Для всех i из множества медоидов: 11 Для всех j из множества немедоидов: 12 Расчет стоимости замены Tm(i,h) 13 Если Tm(i, h) < Tbest: 14 Tbest = Tm(i, j) 15 Запомнить найденные кандидаты: (i_s, j_s) = (i, h) 16 Если Tbest >= 0: 17 Выход 18 Иначе: 19 m = m + {h} - {i}
На фазе BUILD осуществляется построение начального множества медоидов. Данный процесс производится итерационно до тех пор, пока не будет найдено необходимое число медоидов. На фазе SWAP производится попытка улучшить множество выбранных медоидов. Данный процесс также производится итерационно то тех пор, пока целевая функция не перестанет улучшаться. Также, для данного шага можно ввести ограничение по числу производимых алгоритмом итераций.
1.6 Последовательная сложность алгоритма
Для осуществления шага BUILD потребуется:
- n^2 операций сложения и n операций сравнения для выбора начального медоида;
- \sum_{l=1}^{k-1} (2(n-l) \cdot (n-l-1)+(n-l))=\frac{1}{6}(k-1)(4k^2 - 12kn + k + 6n(2n-1)) операций сложения, вычитания и сравнения для всех итераций выбора медоидов.
Таким образом, последовательная сложность шага BUILD оценивается как O(kn^2).
Для осуществления каждого шага SWAP потребуется:
- 2k(n-k)(n-k-1) операций вычитания и сложения;
- k(n-k) операций сравнения;
Таким образом, последовательная сложность каждого шага SWAP оценивается как O(kn^2). Заранее число итераций шага SWAP неизвестно, поэтому принимаем его равным T. Отсюда, общая последовательная сложность алгоритма PAM оценивается как O(Tkn^2).
1.7 Информационный граф
1.7.1 Информационный граф шага BUILD
На рис.1 показана информационная структура шага BUILD алгоритма PAM на некотором шаге.
Операции:
- sum_{o,m_t}(i) = \sum_{j \in o \backslash \{m \cup i\}} \max (D_j, d_{ji}) –– оценка конфигурации при внесении i в множество индексов медоидов m с множеством объектов o;
- \arg \max –– индекс объекта, дающего наибольшую оценку конфигурации при его внесении в множество индексов медоидов m;
- update(m) –– операция добавления индекса объекта в множество индексов медоидов m.
1.7.2 Информационный граф шага SWAP
На рис.2 показана информационная структура шага SWAP алгоритма PAM на некотором шаге.
Операции:
- T_m(i, h) = \sum_{j \in o \backslash \{m \cup h\}} C_{jih} –– стоимость смены конфигурации при замене немедоида h медоидом i в текущей конфигурации m;
- \arg \min –– пара (i, h) (медоид-немедоид), замена которой в текущей конфигурации m дает наименьшую стоимость смены;
- swap –– операция замены медоида i на немедоид h в текущей конфигурации m, если стоимость смены отрицательна.
1.8 Ресурс параллелизма алгоритма
Для осуществления шага BUILD потребуется:
- n параллельных операций сложения и n последовательных операций сравнения для выбора начального медоида;
- \sum_{l=1}^{k-1} 2(n-l) = (k-1)(2n-k) параллельных операций сложения и вычитания для всех итераций выбора медоидов;
- \sum_{l=1}^{k-1} n-l = \frac{1}{2}(k-1)(2n-k) последовательных операций сравнения для всех итераций выбора медоидов.
Таким образом, параллельная сложность шага BUILD оценивается как O(kn).
Для осуществления каждого шага SWAP потребуется:
- k(n-k) параллельных операций вычитания и сложения;
- k(n-k) последовательных операций сравнения.
Таким образом, параллельная сложность каждого шага SWAP оценивается как O(kn). Заранее число итераций шага SWAP неизвестно, поэтому принимаем его равным T. Отсюда, общая параллельная сложность алгоритма PAM оценивается как O(Tkn).
1.9 Входные и выходные данные алгоритма
Входные данные:
- Массив V из \frac{n(n-1)}{2} вещественных чисел, определяющий набор дистанций между всеми парами объектов (сжатая матрица дистанций). Симметрическая матрица дистанций D\in \mathbb{R}^{n\times n} восстанавливается из этого массива однозначным образом (для восстановления необходимо знать число объектов n):
- D(i, j)=\left\{\begin{matrix} V[ni - \frac{i(i + 1)}{2} + (j - i - 1)], & i \lt j\\ V[nj - \frac{j(j + 1)}{2} + (i - j - 1)], & i \gt j \\ 0, & i = j \end{matrix}\right.
- Целое число кластеров k, на которое необходимо разбить множество объектов.
Выходные данные:
- Множество m, состоящее из k индексов объектов, принятых в качестве медоидов. Индекс кластера, которому принадлежит объект с индексом i можно восстановить с использованием функции g_m(i)=\arg \min_{m_j\in m} d_{im_j}.
1.10 Свойства алгоритма
1. Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов является линейным как отношение квадратичной сложности к линейной.
2. Вычислительная мощность последовательного алгоритма, как отношение числа операций к суммарному объему входных и выходных данных: O(Tk) .
3. Алгоритм является устойчивым, так как все операции в алгоритме не подвержены накоплению ошибки.
4. Алгоритм является не детерминированным, так как не детерминирован выбор набора медоидов, на которых достигается наилучшая конфигурация.
5. Имеет высокую вычислительную сложность (квадратичную) ввиду необходимости полного перебора, поэтому неэффективно работает на больших наборах данных.
6. Позволяет работать с произвольными объектами с заданной мерой рассчета расстояний (различий), не требует хранения всего множества объектов.
7. Устойчив к выбросам данных (за счет рассмотрения медоидов).
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Для изучения масштабируемости алгоритма была выполнена его реализация с использованием механизма MPI на языке программирования C++. Данная реализация использует библиотеку Boost (модуль MPI для удобного взаимодействия C++ и MPI и модуль uBLAS для работы с матрицами). Исследование масштабируемости описанной реализации производилось на суперкомпьютере "Ломоносов". Для сборки программы использовался компилятор gcc версии 5.2.0 с опциями "-std=c++11 -O3" совместно с OpenMPI версии 1.8.4.
В качестве рассматриваемого при оценке набора данных была произведена их генерация на основе двумерного нормального распределения. Для этого сперва выбиралось некоторое количество точек, которые в дальнейшем выступали в качестве центроидов кластеров. Далее, для каждого полученного кластера осуществлялась генерация равного числа точек.
Набор значений параметров запуска, используемых для оценке масштабируемости представлен ниже:
- Число процессов: [1, 8, 16, 32, 48, 50, 51, 64, 99, 100, 101, 128, 160, 192, 200, 224, 256, 320, 384, 448, 512]
- Число кластеризуемых элементов: от 1000 до 5000 с шагом 250
- Число кластеров при расчете: 20
Для оценки производительности алгоритма осуществлялся расчет числа операций с плавающей запятой в секунду (FLOPs или GFLOPs). Для этого при каждом запуске рассчитывалось время работы алгоритма, число итераций шага SWAP, по данным значениям можно получить точное число операций сложения, вычитания и сравнения вещественных чисел (оно равно последовательной сложности алгоритма), поделив его на время работы можно получить оценку числа FLOP в секунду. График изменения производительности в зависимости от числа процессоров и числа кластеризуемых элементов представлен ниже. Интерактивный график доступен по ссылке.
Масштабируемость алгоритма была получена путем деления реальной производительности на пиковую произвдительность s задействованных ядер (пиковая производительность одного ядра "Ломоносова" составляет 5.686 GFLOPs). График изменения эффективности в зависимости от числа процессоров и числа кластеризуемых элементов представлен ниже. Интерактивный график доступен по ссылке.
Из полученных значений эффективности можно оценить диапазон эффективности реализации алгоритма:
- минимальная эффективность: 0.10353% достигается при использовании 512 процессов для кластеризации 1000 элементов на 20 кластеров;
- максимальная эффективность: 0.47637% достигается при использовании 1 процесса для кластеризации 2000 элементов на 20 кластеров.
Построим оценки масштабируемости выбранной реализации алгоритма Partitioning Around Medoids согласно Scalability_methodology:
- По числу процессов: 6.07542E-04. При увеличении числа процессов эффективность реализации на рассмотренной области значений параметров запуска возрастает, но интенсивность данного роста мала. Для увеличения масштабируемости по числу процессов необходимо увеличить количество операций в секунду, осуществляемых каждым процессом (например, уменьшив время работы алгоритма). Для этого можно применить различные технологии распараллеливания и векторизации вычислений.
- По размеру задачи: 1.91151E-04. При увеличении размера задачи эффективность возрастает, однако данный рост достаточно слаб. Это говорит нам о том, что эффективность алгоритма слабо зависит от размера входной задачи.
- По двум направлениям: 2.03868E-05. При рассмотрении увеличения как размера входа, так и числа процессов на всей рассмотренной области значений эффективность увеличивается, однако скорость увеличения эффективности небольшая. В совокупности с тем фактом, что разница между минимальной и максимальной эффективностью на рассмотренной области параметров небольшая, эффективность с увеличением масштабов возрастает, но медленно.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
1. Последовательные реализации
- В MATLAB (Commercial software)
- ELKI на языке JAVA (Свободное распространение (AGPL))
- В пакете Cluster на языке R (Свободное распространение (GPL))
- В пакете ClusterR на языке R (Свободное распространение (MIT))
2. Параллельные реализации
3 Литература
- ↑ Kaufman L., Rousseeuw P. J. Finding groups in data: an introduction to cluster analysis. – John Wiley & Sons, 2009. – Т. 344.