Участник:Maria Zaitseva/PAM (Partitioning Around Medoids)

Авторы: Зайцева М.Ф., Ковальчук А.А..

PAM (Partitioning Around Medoids) –– алгоритм разбиения множества объектов на кластеры, базирующийся на использовании наиболее представительных объектов каждого кластера (медоидов) для их описания. Был разработан в 1987 году Леонардом Кауфманом и Питером Русивом . Показывает хорошие результаты разбиения на небольших наборах данных, однако имеет высокую вычислительную сложность, ввиду чего неэффективно работает на больших наборах данных.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Данный алгоритм используется для решения задачи кластеризации множества объектов на заранее известное число кластеров [math]k[/math]. Каждый кластер характеризуется наиболее представительным (центральным ) объектом – медоидом. Принадлежность объекта к соответствующему кластеру определяется индексом наиболее близкого к нему медоида.

На вход алгоритму может подаваться набор объектов с заданной функцией расчета дистанции между ними, либо матрица расстояний, характеризующая дистанции между каждой парой объектов, а также число кластеров, на которое необходимо разбить множество объектов. На выходе алгоритм выдает множество объектов, принятых в качестве медоидов.

Алгоритм состоит из двух последовательных этапов:

1. Шаг BUILD. Построение начального набора [math]k[/math] медоидов путем их последовательного выбора. Первый из них выбирается как объект, сумма дистанций которого до всех других объектов минимальна (центральный объект). Каждый следующий выбирается из оставшихся объектов как лучше всего минимизирующий сумму расстояний от объектов до ближайших к ним медоидов. Выбранный набор медоидов характеризует "конфигурацию" кластеров, для которой может быть вычислена ее стоимость.

2. Шаг SWAP. На данном шаге производится попытка улучшить стоимость текущей конфигурации путем перебора всех возможных замен (медоид-немедоид). Среди рассматриваемых конфигураций ищется наиболее оптимальная. В случае, если данная конфигурация по стоимости лучше текущей, она принимается в качестве текущей и шаг повторяется с начала, иначе алгоритм завершается.

Преимущества данного алгоритма по сравнению с подобными ему:

• В отличие от более популярного алгоритма k-means, PAM позволяет работать с произвольными объектами с заданной мерой рассчета расстояний (различий), не требует хранения всего множества объектов (достаточно знать лишь матрицу дистанций, так как медоиды выбираются из множества объектов), а также более устойчив к выбросам в данных (за счет рассмотрения медоидов вместо центроидов);
• В отличие от традиционного k-medoids на шаге BUILD начальные медоиды выбираются более оптимальным образом по сравнению со случайным выбором. Это позволяет уменьшить количество итераций шага SWAP, тем самым сокращая время работы алгоритма.

Недостатком данного алгоритма является неэффективность при больших наборах данных ввиду необходимости полного перебора.

1.2 Математическое описание алгоритма

Входные данные:

• [math]o = \{1,\dots,n\} \subset \mathbb{Z}[/math] –– множество индексов объектов
• [math]O = \{O_1,\dots,O_n\}[/math] –– множество объектов
• [math]k \leq n[/math] –– количество кластеров для разбиения
• [math]d:O\times O\rightarrow \mathbb{R}^{1}[/math] –– метрика расчета расстояний между объектами, [math]d_{ij} = d(O_i,O_j)[/math]
• [math]D\in \mathbb{R}^{n\times n}[/math] –– симметрическая матрица дистанций объектов, где [math]D=(d_{ij}), i \in o, j \in o[/math]

Выходные данные:

• [math]m = \{m_1,\dots,m_k\}\subset o[/math] –– множество индексов объектов, принятых в качестве медоидов

Принадлежность объекта к определенному кластеру определяется как индекс ближайшего к нему медоида:

[math]g_m(i)=\arg \min_{m_j\in m} d_{im_j}[/math].

Основная задача состоит в выборе такого множества индексов медоидов [math]m[/math], наилучшим образом минимизирующего функционал:

[math]F_o(m) = \sum_{j \in o} d_{jg_m(j)}[/math].

Введем обозначения:

• [math]D_j = d_{jg_m(j)}[/math] –– индекс первого по близости к j медоида
• [math]E_j = d_{jg_{m \backslash g_m(j)}(j)}[/math] –– индекс второго по близости к j медоида

Решение задачи состоит из следующих шагов:

1. Шаг BUILD

 1.1. Выбор первого медоида

[math]m=\{ \arg \min_{i \in o} \sum_{j \in o} d_{ij} \}[/math]

 1.2 Последовательный выбор оставшихся медоидов до тех пор, пока [math]\left\vert{m}\right\vert \neq k[/math]

[math]m = m \cup \{ \arg \max_{i \in o \backslash m} \sum_{j \in o \backslash \{m \cup i\} } \max (D_j - d_{ji}, 0) \}[/math]

2. Шаг SWAP

 2.1. Производится перебор всех возможных пар медоид-немедоид [math](i, h): i \in m, h \in o \backslash m[/math], для каждой из которых рассчитывается стоимость смены текущей конфигурации [math]T_m(i,h)[/math]. При смене конфигурации множество медоидов изменяется [math]m = m \cup \{h\} \backslash \{i\}[/math].

[math]T_m(i, h) = \sum_{j \in o \backslash \{m \cup h\}} C_{jih}[/math], где [math]C_{jih}[/math] –– вклад объекта [math]j[/math] в перестановку медоида [math]i[/math] и не медоида [math]h[/math].

 При этом [math]C_{jih}[/math] рассчитывается по-разному в зависимости от положения [math]j[/math] относительно [math]i[/math] и [math]h[/math] ([math]j[/math] дальше от [math]i[/math] и от [math]h[/math], чем от своего ближайшего медоида; [math]i[/math] оказался ближайшим медоидом [math]j[/math]; [math]j[/math] оказался дальше от [math]i[/math], но ближе к [math]h[/math], чем к своему медоиду).

[math]C_{jih} = \left\{\begin{matrix} 0, & d_{ji} \gt D_j, d_{jh} \gt D_j \\ d_{jh} - d_{ji}, & d_{ji} = D_j, d_{jh} \lt E_j \\ E_j - D_j, & d_{ji} = D_j, d_{jh} \geqslant E_j \\ d_{jh} - D_j, & d_{ji} \gt D_j, d_{jh} \lt D_j \end{matrix}\right.[/math]

 Среди всех пар находится такая пара [math](i_s, h_s)[/math], что [math]T_m(i_s, h_s)[/math] минимально.

 2.2 В случае, если [math]T_m(i_s, h_s) \geq 0[/math], смена конфигурации медоидов не производится и решение задачи окончено. Иначе производится смена конфигурации и повторяется шаг 2.1.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма на этапе BUILD состоит последовательного выбора такого объекта из числа немедоидов, добавление которого к множеству медоидов максимизирует следующую функцию:

[math]F_{m} = \max_{i \in o \backslash m} \sum_{j \in o \backslash \{m \cup i\} } \max (D_j - d_{ji}, 0)[/math]

С каждой следующей итерацией множество просматриваемых немедоидов уменьшается, таким образом, на [math]i[/math]-ом шаге итерации необходимо рассчитывать сумму для [math]n - i[/math] немедоидов.

Вычислительное ядро алгоритма на этапе SWAP состоит в расчете функции минимизации стоимости изменения конфигурации [math]T_m(i, h)[/math] при замене медоида [math]i[/math] на немедоид [math]h[/math] в текущей конфигурации для всех возможных [math](i, h): i \in m, h \in o \backslash m[/math]:

[math]T_m(i, h) = \sum_{j \in o \backslash \{m \cup h\}} C_{jih}[/math].

1.4 Макроструктура алгоритма

Как было указано в описании ядра алгоритма, основную часть метода занимают:

• вычисление [math](k - 1)[/math] медоида [math]\arg \max_{i \in o \backslash m} \sum_{j \in o \backslash \{m \cup i\} } \max (D_j - d_{ji}, 0)[/math];
• поиск оптимальной замены замены медоида на немедоид среди [math]k(n-k)[/math] кандидатов путем вычисления стоимости замены [math]T_m(i, h) = \sum_{j \in o \backslash \{m \cup h\}} C_{jih}[/math] относительно текущей конфигурации [math]m[/math] для каждого кандидата.

1.5 Схема реализации последовательного алгоритма

Псевдокод алгоритма:

Вход: матрица дистанций D; количество кластеров k; максимальное количество итераций алгоритма maxIter
Выход: множество медоидов m
1 # Фаза BUILD
2 Выбор стартового объекта в качестве начального медоида: m = {первый медоид}
3 Пока |m| != k:
4     Выбор следующего медоида i_m
5     Добавление найденного медоида в множество: m = m + {i_m}
6 # Фаза SWAP
7 Пока (maxIter--):
8     Лучшая стоимость замены: Tbest = MAXINT
9     Кандидаты на замену: (i_s, h_s) = (-1, -1)
10     Для всех i из множества медоидов:
11         Для всех j из множества немедоидов:
12             Расчет стоимости замены Tm(i,h)
13             Если Tm(i, h) < Tbest:
14                 Tbest = Tm(i, j)
15                 Запомнить найденные кандидаты: (i_s, j_s) = (i, h)
16     Если Tbest >= 0:
17         Выход
18     Иначе:
19         m = m + {h} - {i}

1.6 Последовательная сложность алгоритма

Для осуществления шага BUILD потребуется:

• [math]n^2[/math] операций сложения и [math]n[/math] операций сравнения для выбора начального медоида;
• [math]\sum_{l=1}^{k-1} 2(n-l) \cdot (n-l-1)=\frac{2}{3}(k-1)(k^2 - 3kn + k + 3(n-1)n)[/math] операций сложения и вычитания для всех итераций выбора медоидов;
• [math]\sum_{l=1}^{k-1} n-l = \frac{1}{2}(k-1)(2n-k)[/math] операций сравнения для всех итераций выбора медоидов.

Таким образом, последовательная сложность шага BUILD оценивается как [math]O(kn^2)[/math].

Для осуществления каждого шага SWAP потребуется:

• [math]2k(n-k)(n-k-1)[/math] операций вычитания и сложения;
• [math]k(n-k)[/math] операций сравнения;

Таким образом, последовательная сложность каждого шага SWAP оценивается как [math]O(kn^2)[/math]. Заранее число итераций шага SWAP неизвестно, поэтому принимаем его равным [math]T[/math]. Отсюда, общая последовательная сложность алгоритма PAM оценивается как [math]O(Tkn^2)[/math].

1.7 Информационный граф

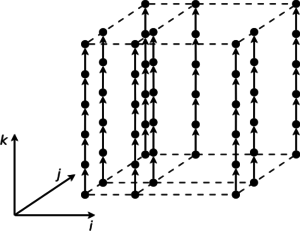
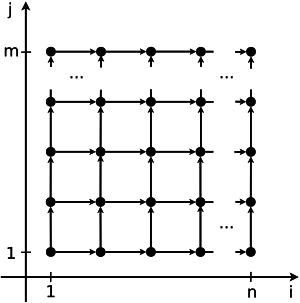
Это очень важный раздел описания. Именно здесь можно показать (увидеть) как устроена параллельная структура алгоритма, для чего приводится описание и изображение его информационного графа (графа алгоритма [1]). Для рисунков с изображением графа будут составлены рекомендации по их формированию, чтобы все информационные графы, внесенные в энциклопедию, можно было бы воспринимать и интерпретировать одинаково. Дополнительно можно привести полное параметрическое описание графа в терминах покрывающих функций [1].

Интересных вариантов для отражения информационной структуры алгоритмов много. Для каких-то алгоритмов нужно показать максимально подробную структуру, а иногда важнее макроструктура. Много информации несут разного рода проекции информационного графа, выделяя его регулярные составляющие и одновременно скрывая несущественные детали. Иногда оказывается полезным показать последовательность в изменении графа при изменении значений внешних переменных (например, размеров матриц): мы часто ожидаем "подобное" изменение информационного графа, но это изменение не всегда очевидно на практике.

В целом, задача изображения графа алгоритма весьма нетривиальна. Начнем с того, что это потенциально бесконечный граф, число вершин и дуг которого определяется значениями внешних переменных, а они могут быть весьма и весьма велики. В такой ситуации, как правило, спасают упомянутые выше соображения подобия, делающие графы для разных значений внешних переменных "похожими": почти всегда достаточно привести лишь один граф небольшого размера, добавив, что графы для остальных значений будут устроены "точно также". На практике, увы, не всегда все так просто, и здесь нужно быть аккуратным.

Далее, граф алгоритма - это потенциально многомерный объект. Наиболее естественная система координат для размещения вершин и дуг информационного графа опирается на структуру вложенности циклов в реализации алгоритма. Если глубина вложенности циклов не превышает трех, то и граф размещается в привычном трехмерном пространстве, однако для более сложных циклических конструкций с глубиной вложенности 4 и больше необходимы специальные методы представления и изображения графов.

В данном разделе AlgoWiki могут использоваться многие интересные возможности, которые еще подлежат обсуждению: возможность повернуть граф при его отображении на экране компьютера для выбора наиболее удобного угла обзора, разметка вершин по типу соответствующим им операций, отражение ярусно-параллельной формы графа и другие. Но в любом случае нужно не забывать главную задачу данного раздела - показать информационную структуру алгоритма так, чтобы стали понятны все его ключевые особенности, особенности параллельной структуры, особенности множеств дуг, участки регулярности и, напротив, участки с недерминированной структурой, зависящей от входных данных.

На рис.1 показана информационная структура алгоритма умножения матриц, на рис.2 - информационная структура одного из вариантов алгоритма решения систем линейных алгебраических уравнений с блочно-двухдиагональной матрицей.

Рис.1. Информационная структура алгоритма умножения матриц

Рис.2. Информационная структура одного из вариантов алгоритма решения систем линейных алгебраических уравнений с блочно-двухдиагональной матрицей

1.8 Ресурс параллелизма алгоритма

Для осуществления шага BUILD потребуется:

• [math]n[/math] параллельных операций сложения и [math]n[/math] последовательных операций сравнения для выбора начального медоида;
• [math]\sum_{l=1}^{k-1} 2(n-l) = (k-1)(2n-k)[/math] параллельных операций сложения и вычитания для всех итераций выбора медоидов;
• [math]\sum_{l=1}^{k-1} n-l = \frac{1}{2}(k-1)(2n-k)[/math] последовательных операций сравнения для всех итераций выбора медоидов.

Таким образом, параллельная сложность шага BUILD оценивается как [math]O(kn)[/math].

Для осуществления каждого шага SWAP потребуется:

• [math]k(n-k) [/math] параллельных операций вычитания и сложения;
• [math]k(n-k)[/math] последовательных операций сравнения.

Таким образом, параллельная сложность каждого шага SWAP оценивается как [math]O(kn)[/math]. Заранее число итераций шага SWAP неизвестно, поэтому принимаем его равным [math]T[/math]. Отсюда, общая параллельная сложность алгоритма PAM оценивается как [math]O(Tkn)[/math].

1.9 Входные и выходные данные алгоритма

В данном разделе необходимо описать объем, структуру, особенности и свойства входных и выходных данных алгоритма: векторы, матрицы, скаляры, множества, плотные или разреженные структуры данных, их объем. Полезны предположения относительно диапазона значений или структуры, например, диагональное преобладание в структуре входных матриц, соотношение между размером матриц по отдельным размерностям, большое число матриц очень малой размерности, близость каких-то значений к машинному нулю, характер разреженности матриц и другие.

1.10 Свойства алгоритма

1. Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов является линейным как отношение квадратичной сложности к линейной.

2. Вычислительная мощность последовательного алгоритма, как отношение числа операций к суммарному объему входных и выходных данных: [math] O(T*k) [/math].

3. Алгоритм является устойчивым, так как все операции в алгоритме не подвержены накоплению ошибки.

4. Алгоритм является не детерминированным, так как не детерминирован выбор набора медоидов, на которых достигается наилучшая конфигурация.

5. Имеет высокую вычислительную сложность (квадратичную), ввиду чего неэффективно работает на больших наборах данных.

2 Программная реализация алгоритма

2.7 Существующие реализации алгоритма

1. Последовательные реализации

• В MATLAB (Commercial software)
• ELKI на языке JAVA (Свободное распространение (AGPL))
• В пакете Cluster на языке R (Свободное распространение (GPL))
• В пакете ClusterR на языке R (Свободное распространение (MIT))

2. Параллельные реализации

• В пакете SPRINT на языке R (Свободное распространение (GPL))