Glossary

1 Algorithm graph

Algorithm graph - a directed acyclic graph the vertices of which correspond to the operations of the algorithm, and the arcs - to the transfer of information between them. Вершины графа алгоритма могут соединяться несколькими дугами, в частности когда в качестве разных аргументов одной и той же операции используется одна и та же величина. Граф алгоритма почти всегда является параметризованным графом. В частности, его вид часто зависит от входных данных.

Граф алгоритма используется как удобное представление алгоритма при исследовании его структуры, ресурса параллелизма, а также других свойств. Его можно рассматривать как параметризованную информационную историю. Он сохраняет её информативность, при это обладая компактностью за счёт параметризации. Разработана методика построения графа алгоритма по исходному тексту программ.

См. также: Граф алгоритма

2 Computational complexity

Computational complexity of a job [math]W[/math] is the number of basic computing steps in the best serial algorithm required to execute the task with a single processor. If we assume, for simplicity, that each basic computing step of a program is executed in a single unit of time, then [math]W=T_1[/math], where [math]T_1[/math] is the execution time of the original serial program.

3 Computational kernel

Computational kernel - the part of algorithm that takes up most of the processing time.

4 Computation locality

Computation locality is the projection of the locality concept to a specific class of data in memory - the instructions that make up a program.

5 Computational intensity

Computational intensity of an algorithm is the ratio of the total number of operations to the total amount of input and output data. The higher the computational intensity, the less the overhead cost of moving data for processing, e.g., on a co-processor, accelerator, or another node within a cluster.

6 Data access locality

Data access locality is the projection of the locality concept to a specific class of data in memory - all the data a program operates with during the course of its execution.

7 Implementation efficiency

Implementation efficiency [math]R_{max}/R_{peak}[/math] is the ratio of real performance [math]R_{max}[/math] achieved for a certain program to the peak performance of the computer used [math]R_{peak}[/math]. This is a very important indicator that describes the quality of computer resource utilization, but gives little insight into the quality of the program's parallelization, which is assessed using other characteristics.

Поскольку пиковая производительность недостижима на практике, эффективность реализации программы всегда меньше единицы. Чем ближе этот показатель к единице, тем лучше для пользователя, поскольку говорит о том, что более эффективно задействованы ресурсы компьютера.

8 Locality (of data access operations)

Locality (of data access operations) is a general assumption of the program's data access properties. When certain data is accessed, there is a high probability the same or nearby data will be accessed soon. The operation of cache memory in particular is based on this assumption. The locality of instructions and data access, as well as spatial and temporal locality, is of importance.

9 Parallel complexity

Parallel complexity - the number of steps needed to execute the algorithm assuming an infinite number of processors (functional units, computing nodes, cores, etc.). The parallel complexity of an algorithm is understood as the height of its canonical parallel form.

10 Parallelization efficiency

Parallelization efficiency [math]E=S/p[/math] is determined as the ratio of the program's speedup [math]S[/math] to the number of processors used [math]p[/math]. It determines the average share of execution time for a parallel algorithm during which the processors are actually used to execute the job. Получение большого ускорения за счёт использования большого числа процессоров зачастую приводит к снижению эффективности.

Если не брать в расчёт эффект super linear speedup, то ускорение выполнения программы не превосходит числа используемых процессоров p, а значит, эффективность распараллеливания не превосходит единицы. Чем ближе этот показатель к единице, тем лучше для пользователя, поскольку говорит о меньшем количестве накладных расходов, а значит, о лучшем качестве распараллеливания программы.

11 Scalability of a parallel program

Scalability of a parallel program is determined in connection with a specific computer and shows how much the dynamic characteristics of the given program change when more computing power is utilized.

Масштабируемость параллельной программы (scalability of parallel program) определяется относительно конкретного компьютера и показывает, как изменяются динамические характеристики данной программы в зависимости от её startup parameters.

Наиболее часто рассматриваемые разновидности масштабируемости параллельных программ: strong scaling, wide scaling, weak scaling.

Если при одновременном увеличении числа процессоров p и computational complexity задачи W parallelization efficiency E остаётся прежней, то данную программу на данном компьютере можно считать масштабируемой.

12 Serial complexity

Serial complexity of algorithm - the number of operations that need to be performed if the algorithm is executed serially.

13 Spatial locality

Spatial locality reflects the average distance between several consecutive memory access operations.

14 Speedup

Speedup [math]S=T_1/T_p[/math], where [math]T_1[/math] is the execution time of the original serial program, [math]p[/math] is the number of processors, [math]T_p[/math] is the execution time of the parallelized program on [math]p[/math] processors.

15 Temporal locality

Temporal locality reflects the average number of access operations for an address in memory during program execution.

16 Determinacy

Детерминированность (determinacy) алгоритма - постоянство структуры вычислительного процесса. Алгоритм выдаёт уникальный и предопределённый результат для заданных входных данных.

17 Redundant computation

Избыточные вычисления (redundant computation) - понятие, которое используют для обозначения разных явлений в параллельных вычислениях.

• В понимании графовой модели вычислений это такие операции, результаты которых нигде не будут использованы. Такие операции появляются в результате ошибок программирования и подлежат удалению из алгоритма.
• Распространено также понимание термина как вычисления, которые выполняются более одного раза или на более чем одном процессоре. Избыточные вычисления могут использоваться либо в многопроцессорных системах, чтобы минимизировать обмены, либо при недостаточном объеме памяти для хранения всех вычисленных значений.
• Кроме этого, избыточными вычислениями можно назвать те операции, которые появляются при замене последовательного алгоритма специальным параллельным, у которого больше операций, но меньший критический путь графа. В таком случае реальное ускорение параллельного алгоритма следует считать не в сравнении с однопроцессорной реализацией его самого, а в сравнении с реализацией последовательного алгоритма.

18 Finite parallelism

Конечный параллелизм (finite parallelism) - параллелизм, определяемый информационной независимостью некоторых фрагментов в тексте программы.

19 Coordinate parallelism

Координатный параллелизм (coordinate parallelism) - частный случай skewed parallelism, определяемый циклами ParDO, при котором информационно независимые вершины лежат на гиперплоскостях, перпендикулярных одной из координатных осей.

20 Mass parallelism

Массовый параллелизм (mass parallelism) - параллелизм, определяемый информационной независимостью итераций циклов программы.

21 Scalability

Масштабируемость (scalability) - способность системы увеличивать свою performance при добавлении ресурсов (обычно аппаратных). Система называется масштабируемой, если она способна увеличивать производительность пропорционально дополнительным ресурсам. Масштабируемость можно оценить через отношение прироста производительности системы к приросту используемых ей ресурсов. Чем ближе это отношение к единице, тем масштабируемость лучше.

22 Wide scaling

Масштабируемость вширь (wide scaling) - зависимость performance R от computational complexity задачи W при фиксированном числе процессоров p (p=const).

23 daps estimation

Оценка daps (daps estimation) - предлагаемая оценка производительности работы с памятью в программе, равна числу выполненных обращений в память в секунду. Построена по аналогии с распространенной оценкой производительности программ — flop/s (floating point operations per second), которая оценивает число операций с плавающей запятой в секунду. Оценка flop/s показывает производительность всей программы с точки зрения производимых вычислений; в то время как daps оценивает производительность программы с точки зрения работы с памятью.

Данная оценка является машинно-зависимой — она вычисляется на основе данных аппаратных датчиков. Служит для проверки точности результатов разрабатываемых нами машинно-независимых оценок локальности, таких как cvg.

24 cvg estimation

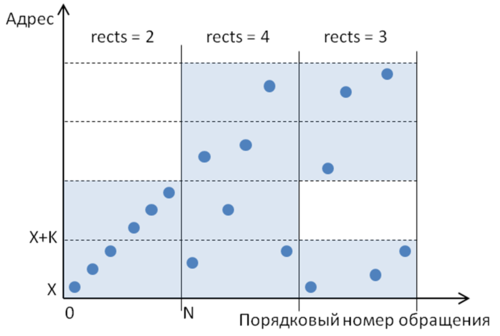
Оценка cvg (cvg estimation) - предлагаемая машинно-независимая оценка локальности обращений в памяти в программе. Рассмотрим первые N обращений в потоке («окно»), и затем разобьем ось ординат (виртуальный адрес обращений) на отрезки длины K – [X .. X+K], [X+K .. X+2K], …, [Y-K .. Y], где [X, Y] - диапазон выделенной под рассматриваемые массивы виртуальной памяти. Таким образом, область построения профиля делится на прямоугольники размером KxN.

Физический смысл такого прямоугольника (при правильно подобранных значениях K и N) заключается в том, что любая последовательность точек, попавших в один прямоугольник, всегда обладает хорошей как пространственной, так и временно́й локальностью. Действительно, при достаточно малом значении K в прямоугольник попадает небольшой локальный фрагмент виртуальной памяти, а, значит, соседние обращения по памяти в любом случае будут расположены близко друг относительно друга. А временна́я локальность внутри прямоугольника не может быть больше N, поэтому при достаточно малом N можно обеспечить и хорошую временну́ю локальность. Однако не имеет смысла брать слишком малые значения для K и N, поскольку в этом случае теряется полезная информация о хорошей локальности не попавшего в прямоугольник фрагмента профиля.

Выделим те прямоугольники, в которые попадает хотя бы одно обращение. Чем меньше таких прямоугольников – тем больше точек попало в одни и те же прямоугольники, тем в общем случае лучше локальность. Пример разбиения профиля на прямоугольники приведен на рис. 1. Здесь для иллюстрации выделено три «окна», в каждом по 6 точек. В первом «окне» всего 2 непустых прямоугольника и самая хорошая локальность их трех вариантов. Во втором «окне» задействованы все 4 прямоугольника, при этом в каждый попало лишь по 1-2 обращения. Третье «окно» включает 3 непустых прямоугольника, и в этом варианте локальность лучше, чем у второго «окна», но хуже, чем у первого.

Рисунок 1. Пример разбиения профиля на прямоугольники

Теперь сдвинем «окно» на одно обращение вправо и снова определим непустые прямоугольники; и так далее для всего профиля обращений. В результате мы получим «покрытие» – последовательность непустых прямоугольников, в каждом из которых содержится хотя бы по одному обращению, т.е. по одной точке профиля.

Далее для каждого «окна» посчитаем число таких непустых прямоугольников (обозначим это число как rects), в результате чего получим последовательность положительных натуральных чисел. Затем посчитаем среднее значение для данной последовательности. Полученное значение назовем оценкой локальности на основе метода покрытий и будем обозначать cvg.

Значение K было решено выбрать равным 64 байт, поскольку это соответствует длине кэш-строки, а в пределах одной кэш-строки пространственная локальность заведомо достаточно хорошая. При этом если запрошено одно значение, то в кэш-память подтянется вся строка из 64 байт, то есть все данные, соответствующие определенному прямоугольнику.

Оптимальное значение N для разных программ может существенно отличаться, но для выполнения корректного сравнения оценка было решено выбрать единственное значение N. Было проведено сравнение результатов для различных значений N, и в результате эмпирическим путем было получено, что наилучшие результаты достигаются при N=512.

25 Startup parameters

Параметры запуска (startup parameters) параллельной программы - параметры, оказывающие влияние на работу параллельной программы, но не влияющие на реализацию алгоритма работы программы (например: размер задачи, число процессов, размер блока, число процессов на узел и т.п.) Параметры запуска по типу можно разделить на:

1. Аппаратные - относящиеся к параметрам аппаратуры.
2. Системные - относящиеся к операционной системе, используемым библиотекам и системным приложениям и их настройкам.
3. Программные - влияющие на логику работы программы или вычислительную сложность задачи, различные параметры, предусмотренные разработчиком.

26 Peak performance

Пиковая производительность (peak performance) [math]R_{peak}[/math] — теоретический предел performance для данного компьютера. Пиковая производительность компьютера вычисляется как сумма пиковых производительностей всех входящих в него вычислительных устройств (процессоров, ускорителей и т.д.). Под пиковой производительностью каждого из вычислительных устройств понимают количество операций в секунду, которые он смог бы теоретически выполнять при полной загрузке всех своих компонент. Надо понимать, что пиковая производительность не только суперкомпьютера, но и, например, любого отдельно взятого процессора является величиной сугубо теоретической, недостижимой на практике.

27 Performance

Производительность (performance) [math]R=Op/t[/math] определяется количеством операций [math]Op[/math], производимых данным компьютером в единицу времени. Для высокопроизводительных вычислений в расчёт обычно берут количество арифметических операций в секунду над вещественными данными, представленными в форме с плавающей точкой. Эта величина называется Flop/s (от английского Floating point operations per second).

Поскольку современные суперкомпьютеры производят очень много таких операций в секунду, их производительность измеряется кратными величинами, такими как GFlop/s ([math]10^9[/math] операций в секунду), TFlop/s ([math]10^12[/math]), PFlop/s ([math]10^15[/math]). Производительность мощнейших современных суперкомпьютеров уже измеряется десятками PFlop/s, активно идёт обсуждение построения систем экзафлопсного (порядка [math]10^18[/math] операций в секунду) уровня производительности.

28 Memory access profile

Профиль обращений в память (memory access profile) - последовательность выполняемых в программе обращений к данным в памяти, расположенных в том порядке, в котором обращения происходят в программе.

Обозначим профиль обращений A = {A₁,A₂,…,A_N}, где N – общее число всех обращений при выполнении программы. Номер i элемента A_i в профиле указывает, каким по счету является данное обращение от начала выполнения программы. Любой элемент А_i будем называть элементом профиля. Запись А_i означает, что данный элемент имеет i-й порядковый номер; данная запись не содержит никакой информации о том, к какой переменной в программе происходит данное обращение.

На данный момент рассматриваются в основном обращения к массивам, поскольку они являются самыми распространенными структурами данных. Каждое обращение представлено в профиле некоторым числом. Таким образом, профиль обращений представляет собой последовательность чисел, которыми могут являться: 1) индексы элементов массива (если профиль строится только для одного массива); 2) виртуальные адреса, к которым происходят обращения; 3) физические адреса. Естественно, в рамках одного профиля используются числа только одного типа.

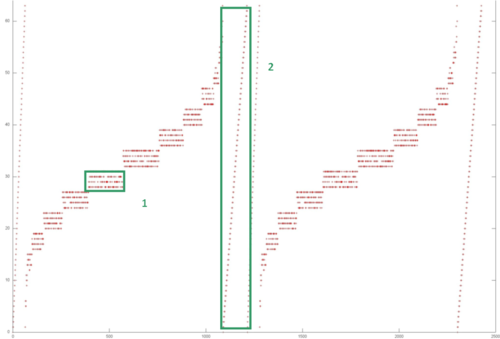
Подобные профили обращений содержат огромное количество полезной информации о работе программы с памятью. Интересным средством анализа профилей является изучение их визуального представления. Пример визуализации профиля приведен на рис. 2. Ось абсцисс — порядковый номер обращения в память, т. е. чем больше номер, тем позже произошло данное обращение. По оси ординат отложен виртуальный адрес памяти, к которому произошло обращение. Каждая точка — это отдельное обращение в память.

Рисунок 2. Визуализация профиля обращений в память

Подобные графики сами по себе могут предоставить интересную информацию о поведении программы. Выделенная на рисунке область 1 (и остальные, аналогичные ей области), скорее всего, обладает хорошей пространственной и временно́й локальностью. Хорошей пространственной — потому что используются только соседние по памяти данные; хорошей временно́й — поскольку повторные обращения к этим данным происходят часто. Область 2 также обладает хорошей пространственной локальностью, поскольку соседние обращения происходят к соседним элементам, однако плохой временно́й локальностью, поскольку повторных обращений к данным просто нет.

Помимо получения данных о локальности, исследование визуализации профилей обращений в память является хорошим средством для понимания и определения шаблонов обращений.

Подобный анализ на основе визуализации профиля обращений помогает понять общее поведение программы, однако он не может дать точной количественной информации о взаимодействии программ с памятью. Для этих целей разрабатываются оценки локальности, такие как daps и cvg.

29 Real performance

Реальная производительность (real performance) [math]R_{max}[/math] — performance данного компьютера на конкретном приложении.

30 Strong scaling

Сильная масштабируемость (strong scaling) - зависимость performance [math]R[/math] от количества процессоров [math]p[/math] при фиксированной computational complexity задачи ([math]W=const[/math]).

31 Skewed parallelism

Скошенный параллелизм (skewed parallelism) - параллелизм в пространстве итераций, определяемый поверхностями уровней разверток.

32 Weak scaling

Слабая масштабируемость (weak scaling) - зависимость performance [math]R[/math] от количества процессоров [math]p[/math] при фиксированной computational complexity задачи в пересчёте на один процессор ([math]W/p=const[/math]).

33 Degree of a vertex

Степень исхода (degree of a vertex) вершины информационного графа - количество исходящих из данной вершины информационных дуг.

34 Super linear speedup

Суперлинейное ускорение (super linear speedup) или сверхлинейное ускорение программы - это speedup, превосходящие число используемых процессоров [math]p[/math]. Чаще всего объясняется эффектом от использования кэш-памяти.

35 Stability

Устойчивость (stability) алгоритма - свойство алгоритма не увеличивать или увеличивать в незначительной степени погрешности, допущенной в начальных данных или допускаемой при вычислениях.

36 Equivalent perturbation

Эквивалентное возмущение (equivalent perturbation) алгоритма - одна из характеристик влияния ошибок округления промежуточных операций на отклонение решения, получаемого алгоритмом, от настоящего решения задачи. Выражается косвенно: влияние ошибок на ответ считается таким же, как если бы данные были заданы с ошибкой, выражаемым эквивалентным возмущением, но задача с такими данными была бы решена точно.

37 Equivalent transformaion

Эквивалентное преобразование (equivalent transformaion) программы - такое преобразование, при котором в точности сохраняется результат выполнения программы.

38 Parallel efficiency

Эффективность распараллеливания (parallel efficiency) [math]E = S/p[/math] (где [math]S[/math] - полученное ускорение работы программы, а [math]p[/math] - число используемых процессоров) определяет среднюю долю времени выполнения параллельного алгоритма, в течение которого процессоры реально используются для решения задачи. Получение большого ускорения за счёт использования большого числа процессоров зачастую приводит к снижению эффективности.

Если не брать в расчёт эффект super linear speedup, то ускорение выполнения программы не превосходит числа используемых процессоров [math]p[/math], а значит, эффективность распараллеливания не превосходит единицы. Чем ближе этот показатель к единице, тем лучше для пользователя, поскольку говорит о меньшем количестве накладных расходов, а значит, о лучшем качестве распараллеливания программы.

39 Canonical parallel form

Ярусно-параллельная форма (ЯПФ) (parallel form) - это представление графа алгоритма, в котором:

• все вершины разбиты на перенумерованные подмножества ярусов;
• начальная вершина каждой дуги расположена на ярусе с номером меньшим, чем номер яруса конечной вершины;
• между вершинами, расположенными на одном ярусе, не может быть дуг.

Высота ЯПФ - это число ярусов. Ширина яруса - число вершин, расположенных на ярусе. Ширина ЯПФ - это максимальная ширина ярусов в ЯПФ.

Канонической ярусно-параллельной формой называется ЯПФ, высота которой на единицу больше длины критического пути, а все входные вершины расположены на первом ярусе. Для заданного графа его каноническая ЯПФ единственна. Высота канонической ЯПФ соответствует parallel complexity алгоритма.