Алгоритм Ланцоша для арифметики с плавающей точкой с полной переортогонализацией

Основные авторы описания: С.А.Айвазян, В.Козлов (Часть 1), А.Ю.Чернявский (компоновка и редактирование), А.С.Антонов (предварительная проверка).

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм Ланцоша – итерационный метод , созданный Корнелиусом Ланцошем, для нахождения собственных значений и собственных векторов симметричной матрицы. Суть алгоритма в том, что он сводит частичную проблему собственных значений симметричной вещественной матрицы к полной проблеме собственных значений для симметричной трехдиагональной матрицы меньшей размерности. Алгоритм применяется к матрицам большой размерности, к которым не применимы никакие прямые методы.

Алгоритм Ланцоша относится к методам аппроксимаций, которые применяют широко распространенную в математике процедуру Релея-Ритца к матричным вычислениям, посредством чего сводят исходную задачу к задаче гораздо меньшего размера, решив которую, получаем приближенные собственные значения и собственные векторы исходной задачи. Метод основан на применении процедуры Релея-Ритца к последовательности вложенных подпространств Крылова. Важной особенностью подпространства Крылова является трехдиагонольность ортогональной проекции на него исходной матрицы, что способствует тому, что процедура Релея-Ритца прорабатывает очень эффективно. Главными особенностями поведения алгоритмов метода Ланцоша являются потеря ортогональности векторов базиса и быстрая сходимость в области наибольших по значению собственных значений. Наиболее популярными средствами борьбы с потерей ортогональности векторов Ланцоша являются различные варианты переортогонализации: частичная, полная и выборочная.

Симметричность исходной матрицы позволяет хранить и вычислять чуть больше половины её элементов, что почти вдвое экономит как необходимые для вычислений объёмы памяти, так и количество операций. Также алгоритм позволяет использовать так называемый режим накопления, обусловленный тем, что значительную часть вычислений составляют вычисления скалярных произведений.

Преимущество алгоритма заключается в том, что он дает приближение за конечное число шагов. Метод Ланцоша выигрывает в конкуренции таким прямым методам, как метод прямых или обратных итераций, [math]QR[/math] и [math]QL[/math] преобразования, методы вращений (вращения Якоби), которые потеряли значение как самостоятельные методы поиска собственных значений матриц большого размера. Также нужно заметить, что метод Ланцоша практически всегда эффективнее других методов аппроксимаций.

1.2 Математическое описание алгоритма

Алгоритм Ланцоша — это итерационный алгоритм поиска [math]k[/math] приближённых собственных значений симметричной вещественной матрицы [math]A[/math] размера [math]n \times n[/math]. Алгоритм применяется, когда матрица [math]A[/math] слишком велика, чтобы к ней можно было применять точные прямые методы вычисления собственных значений. Алгоритм комбинирует метод Рэлея — Ритца поиска приближённых собственных значений и метод Ланцоша построения крыловского подпространства.

Метод Рэлея — Ритца является методом поиска [math]k[/math] приближённых собственных значений симметричной вещественной матрицы [math]A[/math] размера [math]n \times n[/math]. Если [math]Q = [Q_k, Q_u][/math] — ортонормированная матрица размера [math]n \times n[/math], [math]Q_k[/math] имеет размер [math]n \times k[/math], [math]Q_u[/math] имеет размер [math]n \times n - k[/math], то можно записать равенство

[math]T = Q^T A Q = [Q_k, Q_u]^T A [Q_k, Q_u] = \left[ \begin{array}{cc} Q_k^T A Q_k & Q_k^T A Q_u\\ Q_u^T A Q_k & Q_u^T A Q_u \end{array} \right] = \left[ \begin{array}{cc} T_{k} & T_{ku}^T\\ T_{ku} & T_{u} \end{array} \right].[/math]

Метод Рэлея — Ритца заключается в том, что собственные значения матрицы [math]T_k = Q_k^T A Q_k[/math] объявляются приближёнными собственными значениями матрицы [math]A[/math]. Такое приближение является в некотором смысле «наилучшим»: можно показать, что если [math]T_k = V \Lambda V^{-1}[/math] — спектральное разложение [math]T_k[/math], то пара [math](Q_k V, \Lambda)[/math] минимизирует функционал [math]L(P_k, D) = \Vert A P_k - P_k D \Vert_2[/math], причём [math]L(Q_k V, \Lambda) = \Vert T_{ku} \Vert_2[/math], то есть [math]A \approx (Q_k V) \Lambda (Q_k V)^{-1}[/math]. Из этого также видно, что метод Рэлея — Ритца позволяет получать приближения для собственных векторов матрицы [math]A[/math]. Более того, можно показать, что собственные значения [math]T[/math] отличаются от некоторых собственных значений [math]A[/math] не более чем на [math]\Vert T_{ku} \Vert_2[/math].

Метод Ланцоша — это метод построения матрицы [math]Q[/math], при использовании которого, во-первых, матрица [math]T[/math] оказывается симметричной трёхдиагональной, во-вторых, столбцы [math]Q[/math] и [math]T[/math] вычисляются последовательно. Трёхдиагональность [math]T[/math] приводит к следующим явлениям:

1. матрица [math]T_k[/math] является трёхдиагональной матрицей меньшей размерности, а для трёхдиагональных матриц существуют высокоэффективные методы поиска собственных значений;
2. матрица [math]T_{ku}[/math] имеет только один ненулевой (возможно) элемент — правый верхний, а значит, для оценки погрешности полученных собственных значений достаточно знать только этот элемент.

В теории в методе Ланцоша для вычисления каждого следующего столбца [math]q_{j + 1}[/math] матрицы [math]Q[/math] достаточно знать только [math]q_{j - 1}[/math] и [math]q_{j}[/math] в силу трёхдиагональности матрицы [math]T[/math]. На практике из-за ошибок округления, если не предпринимать специальных мер, набор векторов [math]q_{1}, \dots, q_{k}[/math] перестаёт быть ортогональным. Для борьбы с этим явлением на каждом шаге метода Ланцоша приходится выполнять так называемую переортогонализацию — повторно запускать процесс ортогонализации Грама — Шмидта.

Перейдем к описанию самого алгоритма.

Исходные данные: симметричная вещественная матрица [math]A[/math] — матрица, для которой будут вычисляться собственные значения, вектор [math]b[/math] — начальное приближение для метода Ланцоша.

Выходные данные: трёхдиагональная симметричная вещественная матрица [math]T_k = \left[ \begin{array}{cccc} \alpha_1 & \beta_1 & & \\ \beta_1 & \ddots & \ddots & \\ & \ddots & \ddots & \beta_{k - 1}\\ & & \beta_{k - 1} & \alpha_k \end{array} \right][/math], ортонормированный набор векторов [math]q_1, \dots, q_k[/math]: [math]T_k = [q_1, \dots, q_k]^T A [q_1, \dots, q_k][/math].

Формулы метода:

[math] \begin{array}{l} q_1 = b / \Vert b \Vert_2\\ j = \overline{1, k}:\\ \quad z_j = A q_j \\ \quad \alpha_j = q_j^T A q_j = q_j^T z_j \\ \quad z_j' = z_j - \sum_{i=1}^j (z_j^T q_i) q_i \\ \quad z_j'' = z_j' - \sum_{i=1}^j (z_j'^T q_i) q_i\\ \quad \beta_j = \Vert z_j'' \Vert_2\\ \quad q_{j+1} = z_j'' / \Vert z_j'' \Vert_2 = z_j''/\beta_j \end{array} [/math]

Собственные значения и собственные векторы матрицы [math]T_k[/math] ищутся любым прямым алгоритмом.

Вычисление [math]z_j', z_j''[/math] — это полная переортогонализация [math]z_j[/math] методом Грама — Шмидта. Двойной запуск практически гарантирует, что [math]z_j''[/math] будет ортогонален [math]q_1, \dots, q_j[/math]. Заметим, что [math]\sum_{i=1}^j (z^T q_i) q_i = Q_j Q_j^T z[/math], где [math]Q_j = [q_1, \dots, q_j][/math], поэтому переортогонализацию можно переписать в виде [math]z'_j = z_j - Q_j Q_j^T z_j, z_j'' = z_j' - Q_j Q_j^T z_j'[/math].

Если [math]\beta_j = 0[/math] для какого-либо [math]j \lt k[/math], то [math]\Vert T_{ju}\Vert_2 = 0[/math], а значит, собственные значения [math]T_j[/math] в точности совпадают с каким-то собственными значениями [math]A[/math]. В этом случае дальнейшие вычисления прекращаются и либо используется полученная [math]T_j[/math] размерности меньшей, чем [math]k[/math], либо процедура запускается заново с другим начальным вектором [math]b[/math].

1.3 Вычислительное ядро алгоритма

У алгоритма построения матрицы [math]T_k[/math] в том виде, как он описан выше, можно выделить два ядра:

1. умножение матрицы [math]A[/math] на вектор [math]q_j[/math]: [math]z_j = A q_j[/math] ([math]O(n^2)[/math] умножений вещественных чисел);
2. переортогонализация: [math]z'_j = z_j - Q_j Q_j^T z_j,\; z_j'' = z_j' - Q_j Q_j^T z_j'[/math] ([math]O(nk^2)[/math] умножений вещественных чисел).

1.4 Макроструктура алгоритма

На макроуровне выделяем 3 основные операции:

1. Умножение исходной матрицы [math]A[/math] на очередной вектор базиса [math]q_p[/math].

[math] z=Aq_p. [/math]

2. Повторное проведения процесса Грамма-Шмидта для ортогонализации посчитанного вектора [math]z[/math] со всеми построенными ранее векторами базиса.

[math] z =z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i, [/math]

[math]z=z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i. [/math]

3.Непосредственное вычисление нового базисного вектора [math]q_{j+1}[/math] и элементов [math] \alpha_j [/math], [math] \beta_{j+1} [/math] трехдиагональной матрицы.

[math] \alpha_j=q_j^Tz, [/math]

[math]z=z-\alpha_jq_j-\beta_{j}q_{j-1}, [/math]

[math]\beta_{j+1}=||z||, [/math]

[math]q_{j+1}=z/\beta_{j+1}.[/math]

1.5 Схема реализации последовательного алгоритма

Последовательность исполнения метода следующая:

Сначала заполняем начальные значения.

[math] \begin{align} & q_1=b/||b||,\\ & \beta_1=0,\\ &q_0=0, \\ \end{align} [/math]

где [math]b[/math]-произвольный вектор.

Далее выполняется основная процедура, которая строит ортонормированный базис подпространства Крылова для симметричной матрицы и трехдиагональную матрицу размерности [math]k[/math].

Для всех [math]j[/math] от [math]1[/math] до [math]k[/math] по нарастанию выполняются

[math] 1.z=Aq_j, [/math]

Вычисляем элемент, который будет находится на позиции [math]t_{j,j}[/math] конечной матрицы [math]T_k[/math],

[math] 2.\alpha_j=q_j^Tz, [/math]

Чтобы гарантировать ортогональность базиса на каждой итерации цикла два раза проводим полную переортогонализацию, использую процесс Грамма-Шмидта,

[math] 3.z =z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i, [/math]

[math]4.z=z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i, [/math]

После ортогонализации процедура продолжается следующим образом.

[math]5.z=z-\alpha_jq_j-\beta_{j}q_{j-1}, [/math]

Вычисляем элемент, который будет находится на позиции [math]t_{j,j+1}[/math] и [math]t_{j+1,j}[/math],

[math]6.\beta_{j+1}=||z||, [/math]

Если [math]\beta_{j+1}=0[/math], то алгоритм завершается.

[math]7.q_{j+1}=z/\beta_{j+1}.[/math]

В конце каждой итерации получаем очередной вектор [math]q_{j+1}[/math] базиса с единичной нормой, который ортогонален всем предыдущим векторам базиса,

и элементы [math]\alpha_j[/math], [math]\beta_{j+1}[/math] трехдиагональной матрицы размерности [math]k[/math] .

1.6 Последовательная сложность алгоритма

На [math]j[/math]-ой итерации алгоритм выполняет

• [math]n^2 + n + 4nj + n + n = n^2 + 3n + 4nj[/math] умножений и делений;
• [math]n(n - 1) + (n - 1) + (4n - 2)j + (n - 1) = n^2 + (n - 2) + (4n - 2)j[/math] сложений и вычитаний;
• одно извлечение квадратного корня.

Всего за [math]k[/math] итераций алгоритм выполняет

• [math](n + 3)nk + 2nk(k + 1)[/math] умножений и делений;
• [math](n^2 + n - 2)k + (2n - 1)k(k + 1)[/math] сложений и вычитаний.

Таким образом, алгоритм имеет последовательную сложность [math]O(n^2k + nk^2)[/math].

1.7 Информационный граф

Представим информационные графы разных уровней алгоритма.

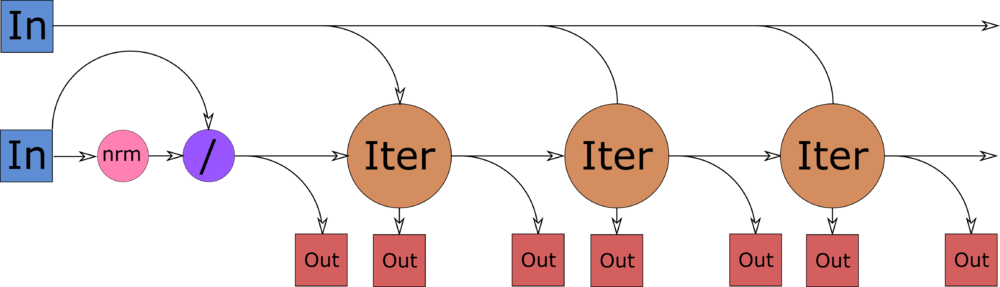
1.7.1 Информационный граф на уровне макроопераций с входными и выходными данными

Рисунок 1. Информационный граф алгоритма Ланцоша на уровне итераций с входными и выходными данными. In — входные данные (матрица [math]A[/math] и вектор [math]b[/math]), Out — выходные данные ([math]\alpha_j, \beta_j[/math] и [math]q_j[/math]), nrm — вычисление еклидовой нормы вектора, / — деление вектора на число, Iter — итерации алгоритма.

1.7.2 Информационный граф на уровне одной итерации с входными и выходными данными

Рисунок 2. Информационный граф итерации алгоритма Ланцоша на уровне макроопераций (первые три итерации). In — входные данные (матрица [math]A[/math]), Out — выходные данные ([math]\alpha_j, \beta_j[/math] и [math]q_j[/math]), dprod — скалярное произведение векторов, mprod — произведение матрицы на вектор, - — разность векторов, nrm — вычисление еклидовой нормы вектора, / — деление вектора на число.

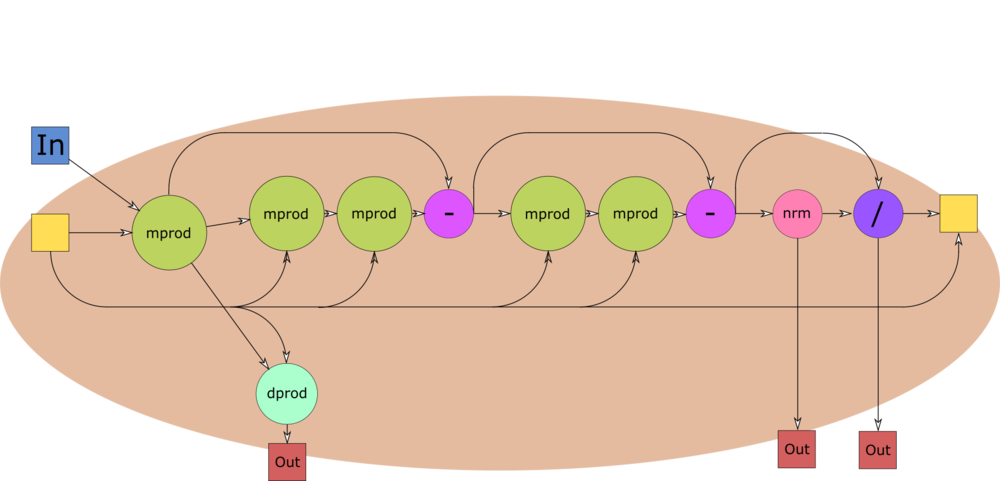
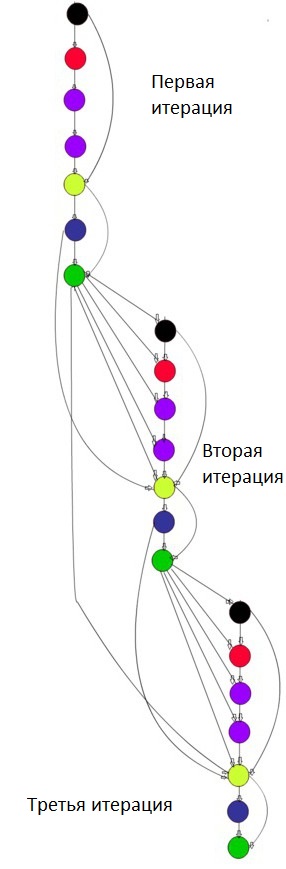
1.7.3 Общий информационный граф алгроитма

Рисунок 3. Общий информационный граф алгроитма алгоритма Ланцоша.

• Вершина черного цвета соответствует операции [math]Aq_j,[/math].
• Вершина красного цвета соответствует операции скалярного произведения [math]q_j^Tz[/math].
• Вершина сиреневого цвета соответствует операции [math]z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i[/math].
• Вершина желтого цвета соответствует операции [math]z-\alpha_jq_j-\beta_{j-1}q_{j-1}[/math].
• Вершина синего цвета соответствует операции [math]||z||[/math].
• Вершина зеленого цвета соответствует операции [math]z/\beta_j[/math].

1.8 Ресурс параллелизма алгоритма

Для реализации [math]j[/math]-ой итерации алгоритма нужно выполнить следующие ярусы:

1. [math]n[/math] ярусов сложений с [math]n[/math] операциями умножения в каждом (вычисление [math]z[/math]);
2. [math]n[/math] ярусов сложений с [math]1[/math] операцией умножения в каждом (вычисление [math]\alpha_j[/math]);
3. [math]j[/math] ярусов сложений с [math]n[/math] операциями умножения в каждом, [math]n[/math] ярусов сложений с [math]j[/math] операциями умножения в каждом, [math]1[/math] ярус вычитаний размера [math]n[/math] (первая переортогонализация);
4. [math]j[/math] ярусов сложений с [math]n[/math] операциями умножения в каждом, [math]n[/math] ярусов сложений с [math]j[/math] операциями умножения в каждом, [math]1[/math] ярус вычитаний размера [math]n[/math] (вторая переортогонализация);
5. [math]n[/math] ярусов сложений с [math]1[/math] операцией умножения в каждом (вычисление [math]\beta_j[/math]);
6. [math]1[/math] ярус делений размера [math]n[/math] (вычисление [math]q_{j + 1}[/math]).

Итого ширина ЯПФ одной итерации составляет [math]O(n)[/math], высота — [math]4n + 2j + 3[/math]. Ширина ЯПФ всего алгоритма составляет [math]O(n)[/math], высота — [math]O(nk + k^2)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные: плотная матрица [math]A[/math] (элементы [math]a_{ij}[/math]),произвольный вектор ненулевой [math]b[/math], количество итераций [math]k[/math].

Дополнительные ограничения:

• [math]A[/math] – симметрическая матрица, т. е. [math]a_{ij}= a_{ji}, i, j = 1, \ldots, n[/math]..

Объём входных данных: [math]\frac{n (n + 3)}{2}[/math] (в силу симметричности достаточно хранить только диагональ и над/поддиагональные элементы).

Выходные данные: трехдиагональная симметрическая матрица [math]T[/math] (элементы [math]_{ij}[/math]), либо два вектора [math]a[/math] и [math]b[/math] размерности [math]k[/math].

Объём выходных данных: [math]2k[/math] (в силу трехдиагональности симметричности достаточно хранить только ненулевые элементы). В разных реализациях эта экономия хранения может быть выполнена разным образом.

1.10 Свойства алгоритма

Сам по себе алгоритм Ланшоца не является устойчивым, так как из-за округлений ортогональность построенных векторов подпространства Крылова быстро теряется, вплоть до того, что некоторые из них становятся линейно зависимыми, что влечет к отсутствию приближения собственных векторов и собственных значений исходной матрицы. Однако, рассмотренный вариант с полной ортогонализацией как раз-таки делает алгоритм устойчивым.

Количество операций умножения и количество операций сложения имеют один и тот же порядок, но они явно преобладают над операцией взятия корня. Также сбалансированы между собой арифметические операции и операции обращений в память. Алгоритм обрабатывает матрицу и вектора и считает множество скалярных произведений, следовательно обеспечивается хорошая сбалансированность операций между параллельными ветвями алгоритма. Соотношение последовательной и параллельной сложности [math]O(n)[/math].

При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных равняется [math]O(k)[/math]. Алгоритм недетерминированный, так как если в какой-то итерации [math]b_j=0[/math], то алгоритм останавливается. Также на недетерминированность может повлиять изменение порядка выполнения ассоциативных операций, в частности при вычислении скалярного произведения.

"Длинных" дуг в информационном графе нет, запись данных происходит предсказуемо(на каждом шаге заполняются следующие элементы выходных векторов), следовательно нет никаких потенциальных сложностей с размещением данных в иерархии памяти компьютера на этапе выполнения программы.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Первое исследование масштабируемости проводилось на 1U сервере со следующими характеристиками:

• 2 x Intel® Xeon® Processor E5-2697 v2;
• 128GB RAM;

Набор изменяемых параметров запуска реализации алгоритма и границы значений параметров алгоритма:

• Число процессоров [math]1,2,4,8,16,32,48[/math]
• Размерность матрицы [math][1000:16000][/math]
• Количество итераций [math]10[/math]

Использовался компилятор g++ версии 5.4.0 с параметрами запуска:

• -fopenmp
• -std=c++11

Реализация алгоритма написана с использованием стандарта OpenMP.

Рисунок 4. Зависимость производительности от числа процессов и размера входной матрицы

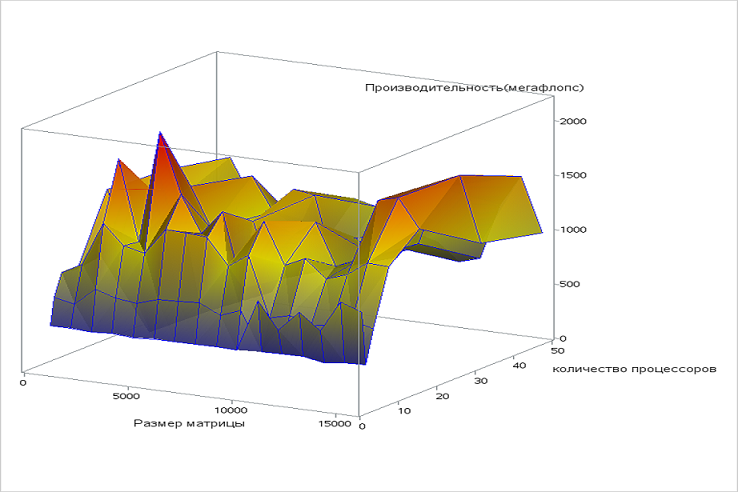
Используемая параллельная реализация алгоритма на языке C++

Как видно из графика, размер задачи не оказывает существенного влияния на производительность. С увеличением количества процессоров производительность сначала возрастает, затем медленно убывает. Высокая производительность достигается при работе 20-30 процессоров, при дальнейшем увеличении числа процессоров накладные расходы на организацию параллельного вычисления ведут к уменьшению производительности.

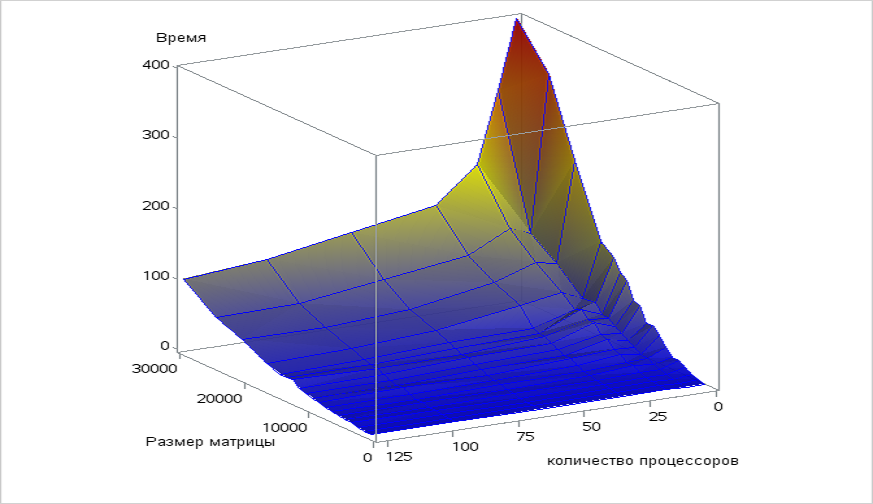
Следующее исследование масштабируемости реализации алгоритма проводилось с использованием стандарта MPI на суперкомпьютере "Ломоносов" суперкомпьютерного комплекса Московского университета.

Набор изменяемых параметров запуска реализации алгоритма и границы значений параметров алгоритма:

• Число процессоров [math]1,2,4,8,16,32,64,96,128[/math]
• Размерность матрицы [math] 1000:15000,1700,21000,25000,30000[/math]
• Количество итераций [math]500[/math]

Сборка осуществлялась с параметрами:

• openmpi/1.5.5-icc
• intel/13.1.0

Рисунок 4. Зависимость производительности от числа процессов и размера входной матрицы

Рисунок 4. Зависимость времени выполнения от числа процессов и размера входной матрицы

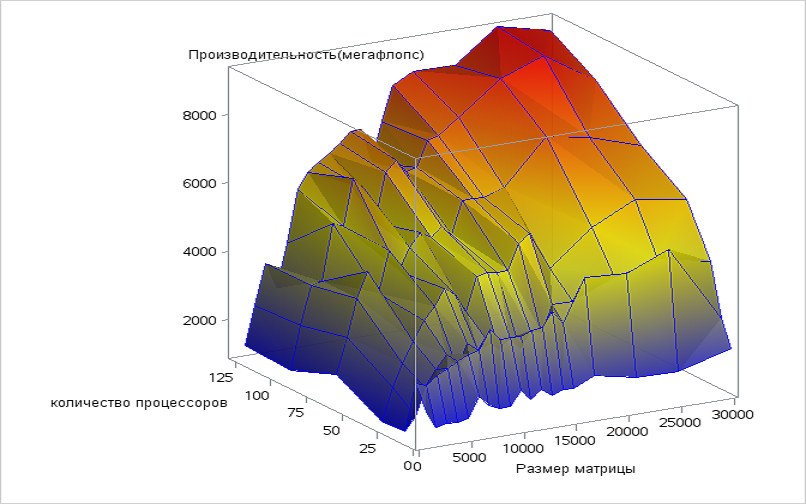
Используемая параллельная реализация алгоритма на языке C++

При увеличении числа процессов производительность возрастает на всей рассмотренной области изменений параметров запуска. Увеличение размера задачи так же повышает производительность в рассматриваемой области, как и при увеличении количества процессоров, но при размерах задачи больше 25000 наблюдается медленный спад. Это снижение производительности объясняется тем, что при увеличении размера задачи существенно возрастают объемы передаваемых данных между процессами.

2.7 Существующие реализации алгоритма

NAG Library имеет множество процедур для решения система алгебраических уравнений и нахождения собственных значений, которые используют алгоритм Ланцоша.

http://www.nag.com/content/nag-library C, C++, Fortran, C#, MATLAB, R.

MATLAB содержит реализацию алгоритма в пакете Gaussian Belief Propagation Matlab Package.

http://www.cs.cmu.edu/~bickson/gabp/.

GraphLab имеет библиотеку, в которой есть огромное количество параллельных реализаций алгоритма Ланцоша

https://turi.com/products/create/open_source.html C++.

В LANSO/PLANSO есть параллельная версия алгоритма

http://web.cs.ucdavis.edu/~bai/ET/lanczos_methods/overview_PLANSO.html Fortran.

3 Литература

<references \>