Алгоритм Пейли построения матрицы Адамара
| Алгоритм Пейли построение матрицы Адамара | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(n^2)[/math] |
| Объём входных данных | [math]1[/math] |
| Объём выходных данных | [math]n^2[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(1)[/math] |
| Ширина ярусно-параллельной формы | [math]O(n^2)[/math] |
Основные авторы описания: Иванов Н.В. (Разделы 1.1,1.7,1.9,1.10,2.4,2.7), Цыганов Н.И. (Разделы 1.2,1.3,1.4,1.5,1.6,1.7,1.8,2.4), А.Ю.Чернявский (проверка, редактирование), С.Н.Леоненков (предварительня проверка),
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Матрицы Адамара были введены в математический обиход в конце прошлого века и играют важную роль в алгебре и комбинаторике. Они находят широкое применение в теории кодирования (коды, исправляющие ошибки), теории планирования многофакторных экспериментов (блок-схемы) и других областях математики.[1] Сравнительно недавно (в 1960 г.) было замечено, что эти матрицы могут быть использованы для построения кодов с большим кодовым расстоянием.
Матрицей Адамара порядка n называется [math]n*n[/math] матрица [math]H[/math], элементами которой являются +1 и −1 такая, что [math]H H^T = n E_n[/math], где [math]E_n[/math] - единичная матрица размера n.
Матрица Адамара обладает следующими свойствами:
- Различные строки матрицы ортогональны
- Скалярное произведение любой строки саму на себя равно n
- Умножение любой строки или столбца на -1 переводит H в другую матрицу Адамара
- Если все элементы первой строки и первого столбца равны +1, то матрица Адамара называется нормализованной
Ниже показаны примеры нормализованных матриц Адамара порядка 1,2 и 4, причем нормализованность матриц сохраняется при перестановке любых строк и столбцов, кроме первых:
[math]H_1 = (1)[/math] [math], H_2 = \begin{pmatrix} 1 & 1\\ 1 & -1\end{pmatrix} [/math], [math], H_4 = \begin{pmatrix} 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1\end{pmatrix} [/math]
Предполагается, что существуют матрицы Адамара порядка 1, 2 и всех порядков n, кратных 4, хотя это до сих пор еще не было доказано. Нет универсального алгоритма построения матрицы Адамара произвольного размера, но известно большое число методов для различных частных случаев, и наименьший порядок, для которого матрица Адамара еще не построена, равен 268 (на 1977 г.). [2] М
В данном описании рассматривается метод Пейли, основанный на теоретико-числовых принципах и позволяющий строить матрицы Адамара порядка [math]n=p+1[/math], кратного 4, где p-простое число.
1.2 Математическое описание алгоритма
Для решения поставленной задачи будем использовать метод Пейли. Это построение дает матрицы Адамара любого порядка [math]n=p+1[/math], кратного 4, где p-простое число.
Определение. Пусть p-простое число. Ненулевые квадраты чисел, приведенные по модулю p, называются квадратичными вычетами по модулю p или просто вычетами по модулю p.
Чтобы найти все вычеты по модулю p, достаточно рассмотреть квадраты чисел от [math]1^2[/math] до [math](p-1)^2[/math]. Но если учесть, что [math](p-a)^2 [/math] [math]mod [/math] [math] p = (-a)^2 [/math] [math] mod [/math] [math] p = a^2 [/math] [math]mod[/math] [math] p[/math], то достаточно рассмотреть лишь числа [math]1^2[/math] [math]mod[/math] [math]p, 2^2[/math] [math]mod[/math] [math]p, ... , (\frac{p-1}{2})^2[/math] [math] mod [/math] [math]p[/math] .
Функция [math]X(i)[/math], называемая символом Лежандра, определяется на целых числах следующим образом:
- [math]X(i)=0[/math], если i кратно p;
- [math]X(i)=1[/math], если остаток от деления i на p является квадратным вычетом по модулю p;
- [math]X(i)=-1[/math], если остаток от деления i на p является невычетом.
Теперь мы построим матрицу Джекобстола [math]Q=(q_{ij})[/math]. Она представляет собой [math](p*p)[/math]-матрицу, строки и столбцы которой пронумерованы числами 0,1,..., p-1, а элементы [math]q_{ij}=X(j-i)[/math].
Пусть теперь [math] H = \begin{pmatrix} 1 & 1\\ 1^T & Q-I\end{pmatrix} [/math].
Все элементы главной диагонали этой матрицы, кроме элемента [math]h_{00}[/math], равны [math]X(0)-1=-1[/math]. Нетрудно заметить, что данная матрица состоит только лишь из элементов 1 и -1.
Доказано, что такая матрица [math]H[/math] представляет собой нормализованную матрицу Адамара порядка p+1, которую называют матрицей типа Пейли.[3]
Исходные данные алгоритма - это порядок генерируемой матрицы Адамара [math]n[/math], удовлетворяющее следующим свойствам:
- [math]n\gt 0[/math];
- [math]n[/math] делится на 4;
- [math]n-1[/math] - простое число.
Вспомогательные данные:
- Число [math]p=n-1[/math];
- Вектор квадратичных вычетов (по модулю [math]p[/math]) [math]R[/math] (элементы [math]r_i[/math]) размера [math]2p[/math]. В этом векторе индексация идёт с нуля.
Вычисляемые данные:
- Матрица Адамара [math]H[/math] (элементы [math]h_{ij}[/math]) размера [math]n \times n[/math]. Индексация строчек и столбцов идёт с нуля.
Алгоритм:
- 1. Строится вектор квадратичных вычетов [math]R[/math].
- Первые [math]p[/math] элементов вектора [math]R[/math] ([math]i=0,1,...,p-1[/math]) определяются следующим образом:
- [math]r_i=1[/math], если [math]i \in \{1^2[/math] [math]mod[/math] [math]p, 2^2[/math] [math]mod[/math] [math]p, ... , (\frac{p-1}{2})^2[/math] [math] mod[/math] [math] p\}[/math], [math]i=0,1,...,p-1[/math], то есть если [math]i[/math] является квадратичным вычетом по модулю [math]p[/math];
- [math]r_i=-1[/math], иначе.
- Вторые [math]p[/math] элементов ([math]i=p,1,...,2p-1[/math]) являются копией первых [math]p[/math] элементов:
- [math]r_i=r_{i-p}, i=p,1,...,2p-1.[/math]
- Первые [math]p[/math] элементов вектора [math]R[/math] ([math]i=0,1,...,p-1[/math]) определяются следующим образом:
- 2. Строится матрица Адамара [math]H[/math].
- Элементы матрицы Адамара [math]H[/math] находятся следующим образом:
- [math]h_{0j}=1, j=0,1, ... ,n-1;[/math]
- [math]h_{i0}=1, i=1,2, ... ,n-1;[/math]
- [math]h_{ij}=r_{j-i+p}, i=1,2, ... ,n-1, j=1,2, ... ,n-1.[/math]
- Элементы матрицы Адамара [math]H[/math] находятся следующим образом:
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма состоит из [math](n-1) \times (n-1)[/math] операций присваивания следующего вида:
- [math]h_{ij}=r_{j-i+p},[/math] [math] i=1,2, ... ,n-1, j=1,2, ... ,n-1.[/math]
1.4 Макроструктура алгоритма
Как видно из математического описания, алгоритм основан на простейших операциях с числами, поэтому макроструктура алгоритма полностью соответствует его математическому описанию.
1.5 Схема реализации последовательного алгоритма
Приведем процедуру на языке С++, реализующую описанный алгоритм. На вход процедуре подается порядок матрицы [math]n[/math] и ссылка на заполняемую матрицу [math]result[/math]. Считаем, что [math]n[/math] положительно, делится на [math]4[/math], [math]n-1[/math] - простое число, а размер матрицы [math]result[/math] равен [math]n \times n[/math].
void buildHadamardMatrix(int n, vector< vector<int> > & result)
{
// 1) matrix size changing
result.resize(n);
for (int i=0; i<n; i++) {
result[i].resize(n);
}
// 2) residue array building
int p=n-1;
vector<int> residues;
residues.resize(2*p);
for (int i=0; i<p; i++) {
residues[i] = -1;
}
for (int i=1; i<= (p-1)/2; i++) {
residues[i*i % p] = 1;
}
for (int i=p; i<2*p; i++) {
residues[i] = residues[i-p];
}
// 3) Paley matrix building
// first line filling
for (int j=0; j<n; j++) {
result[0][j] = 1;
}
// first column filling
for (int i=1; i<n; i++) {
result[i][0] = 1;
}
// others
for (int i=1; i<n; i++) {
for (int j=1; j<n; j++) {
result[i][j] = residues[j-i+p];
}
}
}
1.6 Последовательная сложность алгоритма
Под сложностью будем понимать зависимость числа операций от задаваемого порядка матрицы [math]n[/math].
Основными операциями алгоритма являются:
- [math]\frac{n}{2}-2[/math] операций умножения;
- [math]\frac{n}{2}-2[/math] операций взятия остатка;
- [math]n^2+\frac{5}{2}n-3[/math] операций присваивания.
Из чего следует, что алгоритм имеет квадратичную последовательную сложность.
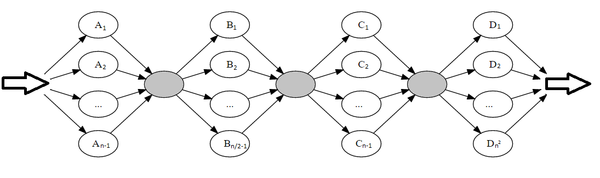
1.7 Информационный граф
Информационный граф алгоритма можно представить в виде четырёх последовательных блоков. Первый блок содержит [math]n-1[/math] параллельных ветвей, второй блок - [math]\frac{n}{2}-1[/math] параллельных ветвей, третий - [math]n-1[/math] и четвёртый - [math]n^2[/math].
Каждая вершина из [math]A_1-A_{n-1}[/math], [math]C_1-C_{n-1}[/math], [math]D_1-D_{n^2}[/math] соответствует операции присваивания, каждая вершина из [math]B_1-B_{\frac{n}{2}-1}[/math] соответствует трём последовательным операциям: умножения, взятия остатка по модулю и присваивания, а вершины, окрашенные серым, представляют собой промежуточные точки синхронизации.
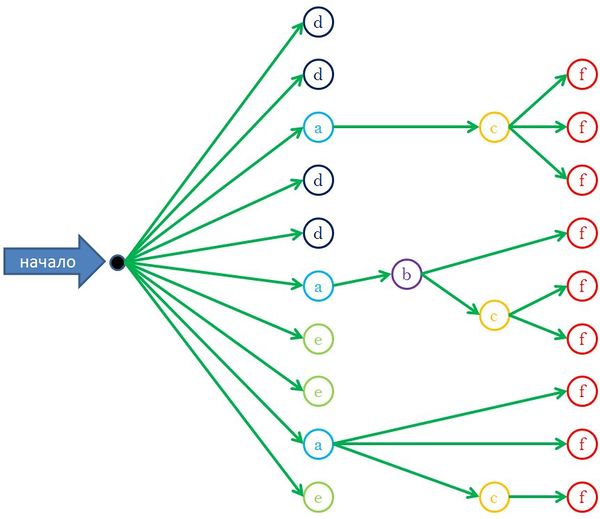
На рисунке приведен информационный граф алгоритма для случая n=4. Вершины графа соответствуют следующим строчкам кода:
a. residues[i] = -1;
b. residues[i*i%p] = 1;
c. residues[i] = residues[i-p];
d. result[0][j] = 1;
e. result[i][0] = 1;
f. result[i][j] = residues[i-j+p];
1.8 Ресурс параллелизма алгоритма
Как видно из информационного графа алгоритма, в параллельном варианте необходимо последовательно выполнить следующие блоки:
- [math]n-1[/math] операций присваивания;
- [math]\frac{n}{2}-1[/math] участков, состоящих из трёх операций: умножения, взятия остатка и присваивания;
- [math]n-1[/math] операций присваивания;
- [math]n^2[/math] операций присваивания.
Из этого можно сделать вывод, что высота ярусно-параллельной формы информационного графа равняется 6 (присваивание, умножение, взятие остатка, присваивание, присваивание, присваивание). Ширина ярусно-параллельной формы равняется [math]n^2[/math], что означает, что при использовании [math]n^2[/math] процессоров матрица Адамара будет строиться за 6 операций.
1.9 Входные и выходные данные алгоритма
Входные данные: число [math]n[/math] - порядок матрицы Адамара [math]H_n[/math]. Дополнительные ограничения на [math]n[/math]:
- [math]n[/math] - натуральное;
- [math]n[/math] делится на 4;
- [math]n-1[/math] - простое.
Объем входных данных: 1 (число [math]n[/math]).
Выходные данные: построенная матрица Адамара [math]H_n[/math] (её элементы [math]h_{ij}[/math]).
Объем выходных данных: [math]n^2[/math] (количество элементов матрицы Адамара размера [math]n*n[/math]).
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов является квадратичным.
Вычислительная мощность алгоритма является постоянной ([math]O(1)[/math]).
Алгоритм является полностью детерминированным.
Для вершин [math]A_1-A_{n-1}[/math], [math]B_1-B_{\frac{n}{2}-1}[/math], [math]C_1-C_{n-1}[/math] информационного графа степени исхода являются линейными, что означает, что при возможности на этапе реализации необходимо позаботиться об эффективном доступе к элементам массива "[math]residues[/math]".
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Исследование масштабируемости параллельной реализации алгоритма построения матрицы Адамара проводилось на суперкомпьютере «Ломоносов». Для этого была исследована собственная реализация алгоритма с использованием средств MPI. В ходе исследования было произведено множество запусков программы с различными значениями параметра [math]n[/math] (размер матрицы Адамара) и числом процессоров.
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
- число процессоров (p): [2,64] с шагом 2;
- размер матрицы: простые числа в диапазоне [4,10000].
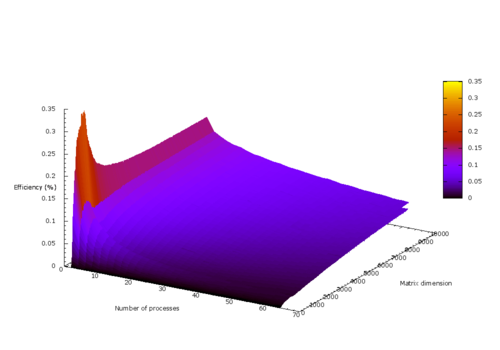
В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма:
- минимальная эффективность реализации 0.0000036% при n=4, p=2;
- максимальная эффективность реализации 0.333426% при n=948, p=2.
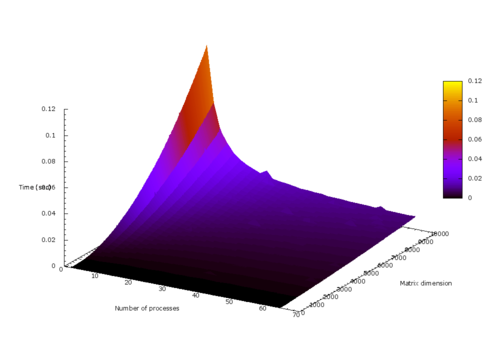
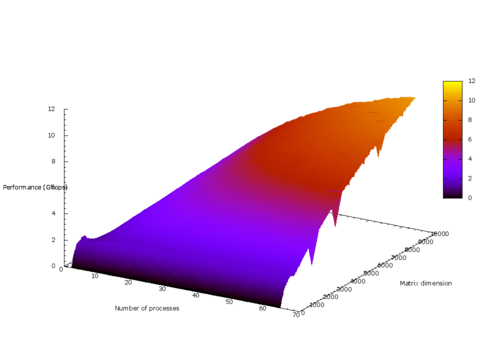
Ниже представлены графики времени работы, производительности и эффективности данной реализации алгоритма построения матрицы Адамара в зависимости от изменяемых параметров запуска.
Исследованная параллельная реализация на языке C++
Построим оценки масштабируемости, используя полученные результаты:
- По размерности задачи. Увеличение размерности задачи приводит к увеличению производительности.
- По числу процессоров. С ростом числа процессоров растет производительность, но при малых размерностях задачи этот рост незначителен. Это связано с дополнительными издержками по записи в участок памяти каждого процессора вспомогательного массива вычетов, а также с обменом информации между процессорами.
- По двум направлениям. При увеличении как числа процессоров, так и размерности задачи, производительность увеличивается. Причем чем больше используется процессоров, тем сильнее увеличивается производительность при увеличении размерности.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Алгоритм построения матрицы Адамара реализован в различных математических пакетах и библиотеках:
- MATLAB (вносятся дополнительные ограничения, когда n, или n/12, или n/20 являются степенями по основанию 2)
- R
- Wolfram Mathematica
- SciPy для Python
3 Литература
- ↑ http://cyberleninka.ru/article/n/matritsy-adamara-nechetnogo-poryadka.pdf
- ↑ Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки: Пер. с англ. — М: Связь, 1979. — c. 52-57
- ↑ http://tc.nsu.ru/uploads/codingtheory.pdf