Алгоритм k средних (k-means)

Основные авторы статьи: Д.Бротиковская, Д.Зобнин.

Алгоритм [math]k[/math] средних (k-means)
Последовательный алгоритм
Последовательная сложность	[math]O(ikdn)[/math]
Объём входных данных	[math] dn [/math]
Объём выходных данных	[math] n [/math]

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм k средних (англ. k-means) - один из алгоритмов машинного обучения, решающий задачу кластеризации. Этот алгоритм является неиерархическим, итерационным методом кластеризации, он получил большую популярность благодаря своей простоте, наглядности реализации и достаточно высокому качеству работы. Был изобретен в 1950-х годах математиком Гуго Штейнгаузом и почти одновременно Стюартом Ллойдом. Особую популярность приобрел после публикации работы МакКуина в 1967.

Алгоритм представляет собой версию EM-алгоритма, применяемого также для разделения смеси гауссиан. Основная идея алгоритма k-means заключается в том, что данные произвольно разбиваются на кластеры, после чего итеративно перевычисляется центр масс для каждого кластера, полученного на предыдущем шаге, затем векторы разбиваются на кластеры вновь в соответствии с тем, какой из новых центров оказался ближе по выбранной метрике.

Цель алгоритма заключается в разделении [math]n[/math] наблюдений на [math]k[/math] кластеров таким образом, чтобы каждое наблюдение принадлежало ровно одному кластеру, расположенному на наименьшем расстоянии от наблюдения.

1.2 Математическое описание алгоритма

Дано:

• набор из [math]n[/math] наблюдений [math]X=\{\mathbf{x}_1, \mathbf{x}_2, ..., \mathbf{x}_n\}, \mathbf{x}_i \in \mathbb{R}^d, \ i=1,...,n[/math];
• [math]k[/math] - требуемое число кластеров, [math]k \in \mathbb{N}, \ k \leq n[/math].

Требуется:

Разделить множество наблюдений [math]X[/math] на [math]k[/math] кластеров [math]S_1, S_2, ..., S_k[/math]:

• [math]S_i \cap S_j= \varnothing, \quad i \ne j[/math]

• [math]\bigcup_{i=1}^{k} S_i = X[/math]

Действие алгоритма:

Алгоритм k-means разбивает набор [math]X[/math] на [math]k[/math] наборов [math]S_1, S_2, ..., S_k,[/math] таким образом, чтобы минимизировать сумму квадратов расстояний от каждой точки кластера до его центра (центр масс кластера). Введем обозначение, [math]S=\{S_1, S_2, ..., S_k\}[/math]. Тогда действие алгоритма k-means равносильно поиску:

[math]\arg\min_{S} \sum\limits_{i=1}^k \sum\limits_{\mathbf{x} \in S_i} \rho(\mathbf{x}, \mathbf{\mu}_i )^2,[/math]

[math](1)[/math]

где [math]\mathbf{\mu}_i[/math] – центры кластеров, [math]i=1,...,k, \quad \rho(\mathbf{x}, \mathbf{\mu}_i)[/math] – функция расстояния между [math]\mathbf{x}[/math] и [math]\mu_i[/math]

Шаги алгоритма:

1. Начальный шаг: инициализация кластеров

   Выбирается произвольное множество точек [math]\mu_i, \ i=1,...,k,[/math] рассматриваемых как начальные центры кластеров: [math]\mu_i^{(0)} = \mu_i, \quad i=1,...,k[/math]

2. Распределение векторов по кластерам

   Шаг [math]t: \forall \mathbf{x}_i \in X, \ i=1,...,n: \mathbf{x}_i \in S_j \iff j=\arg\min_{k}\rho(\mathbf{x}_i,\mathbf{\mu}_k^{(t-1)})^2[/math]

3. Пересчет центров кластеров

   Шаг [math]t: \forall i=1,...,k: \mu_i^{(t)} = \cfrac{1}{|S_i|}\sum_{\mathbf{x}\in S_i}\mathbf{x}[/math]

4. Проверка условия останова:
   • if [math]\exists i\in \overline{1,k}: \mu_i^{(t)} \ne \mu_i^{(t-1)}[/math] then
     • [math]t = t + 1[/math];
     • goto 2;
   • else
     • stop

1.3 Вычислительное ядро алгоритма

Вычислительным ядром являются шаги 2 и 3 приведенного выше алгоритма: распределение векторов по кластерам и пересчет центров кластеров.

Распределение векторов по кластерам предполагает вычисление расстояний между каждым вектором [math]\mathbf{x}_i \in X, \ i= 1,...,n[/math] и центрами кластера [math]\mathbf{\mu}_j, \ j= 1,...,k[/math]. Таким образом, данный шаг предполагает [math]kn[/math] вычислений расстояний между [math]d[/math]-мерными векторами.

Пересчет центров кластеров предполагает [math]k[/math] вычислений центров масс [math]\mathbf{\mu}_i[/math] множеств [math]S_i, \ i=1,...,k,[/math] представленных выражением в шаге 3 представленного выше алгоритма.

1.4 Макроструктура алгоритма

Инициализация центров масс [math]\mu_1, ..., \mu_k[/math].

Наиболее распространенными являются следующие стратегии:

• Метод Forgy
  В качестве начальных значений [math]\mu_1, ..., \mu_k[/math] берутся случайно выбранные векторы.
• Метод случайно разделения (Random Partitioning)
  Для каждого вектора [math]\mathbf{x}_i \in X, \ i=1,...,n,[/math] выбирается случайным образом кластер [math]S_1, ..., S_k[/math], после чего для каждого полученного кластера вычисляются значения [math]\mu_1, ..., \mu_k[/math].

Распределение векторов по кластерам

Для этого шага алгоритма между векторами [math]\mathbf{x}_i \in X, \ i=1,...,n,[/math] и центрами кластеров [math]\mu_1,...,\mu_k[/math] вычисляются расстояния по формуле (как правило, используется Евлидово расстояние):

[math] \mathbf{v}_1, \mathbf{v}_2 \in \mathbb{R}^d, \quad \rho(\mathbf{v}_1, \mathbf{v}_2) = \lVert \mathbf{v}_1- \mathbf{v}_2 \rVert= \sqrt{\sum_{i=1}^{d}(\mathbf{v}_{1,i} - \mathbf{v}_{2,i})^2}[/math]

[math](2)[/math]

Пересчет центров кластеров

Для этого шага алгоритма производится пересчет центров кластера по формуле вычисления центра масс:

[math] \mu = \cfrac{1}{|S|}\sum_{\mathbf{x}\in S}\mathbf{x}[/math]

[math](3)[/math]

1.5 Схема реализации последовательного алгоритма

1. Инициализировать центры кластеров [math]\mathbf{\mu}_i^{(1)}, \ i=1,...,k[/math]
2. [math]t \leftarrow 1[/math]
3. Распределение по кластерам
[math]\quad S_i^{(t)}=\{\mathbf{x}_p: \lVert\mathbf{x}_p-\mathbf{\mu}_i^{(t)}\rVert^2 \leq \lVert\mathbf{x}_p-\mathbf{\mu}_j^{(t)}\rVert^2 \quad \forall j=1,...,k\},[/math]
[math]\quad[/math]где каждый вектор [math]\mathbf{x}_p[/math] соотносится единственному кластеру [math]S^{(t)}[/math]
4. Обновление центров кластеров
[math]\quad \mathbf{\mu}_i^{(t+1)} = \frac{1}{|S^{(t)}_i|} \sum_{\mathbf{x}_j \in S^{(t)}_i} \mathbf{x}_j [/math]
5. if [math]\exists i \in \overline{1,k}: \mathbf{\mu}_i^{(t+1)} \ne \mathbf{\mu}_i^{(t)}[/math] then
[math]\quad t = t + 1[/math];
[math]\quad[/math]goto 3;
[math]~~~[/math]else
[math]\quad[/math]stop

1.6 Последовательная сложность алгоритма

Обозначим [math]\Theta_{\rm centroid}^{d, m}[/math] временную сложность вычисления центорида кластера, число элементов которого равна [math]m[/math], в d-мерном пространстве.

Аналогично [math]\Theta_{\rm distance}^d[/math] – временная сложность вычисления расстояния между двумя d-мерными векторами.

Сложность шага инициализации [math]k[/math] кластеров мощности [math]m[/math] в d-мерном пространстве – [math]\Theta_{\rm init}^{k, d, m}[/math]

• Стратерия Forgy: вычисления не требуются, [math]\Theta_{\rm init}^{k, d, m} = 0[/math]
• Стратегия случайного разбиения: вычисление центров [math]k[/math] кластеров, [math]\Theta_{\rm init}^{k, d, m} = k \cdot \Theta_{\rm centroid}^{d, m}, m \le n[/math]

Cложность шага распределения d мерных векторов по [math]k[/math] кластерам – [math]\Theta_{\rm distribute}^{k, d}[/math]

На этом шаге для каждого вектора [math]\mathbf{x}_i \in X, \ i=1,...,n,[/math] вычисляется [math]k[/math] расстояний до центров кластеров [math]\mathbf{\mu}_1, ...\mathbf{\mu}_k[/math]

[math]\Theta_{\rm distribute}^{k, d} = n \cdot k \cdot \Theta_{\rm distance}^d[/math]

Сложность шага пересчета центров [math]k[/math] кластеров размера [math]m[/math] в d-мерном пространстве – [math]\Theta_{\rm recenter}^{k, d, m}[/math]

На этом шаге вычисляется [math]k[/math] центров кластеров [math]\mathbf{\mu}_1, ...\mathbf{\mu}_k[/math]

[math]\Theta_{\rm recenter}^{k, d, m} = k \cdot \Theta_{\rm centroid}^{d, m}[/math]

Рассчитаем [math]\Theta_{\rm centroid}^{d, m}[/math] для кластера, число элементов которого равно [math]m[/math]

[math]\Theta_{\rm centroid}^{d, m}[/math] = [math]m \cdot d[/math] сложений + [math]d[/math] делений

Рассчитаем [math]\Theta_{\rm distance}^d[/math] в соответствие с формулой [math](2)[/math]

[math]\Theta_{\rm distance}^d[/math] = [math]d[/math] вычитаний + [math]d[/math] умножений + [math](d-1)[/math] сложение

Предположим, что алгоритм сошелся за [math]i[/math] итераций, тогда временная сложность алгоритма [math]\Theta_{\rm k-means}^{d, n}[/math]

[math]\Theta_{\rm k-means}^{d, n} \le \Theta_{\rm init}^{k, d, n} + i(\Theta_{\rm distribute}^{k, d} + \Theta_{\rm recenter}^{k, d, n})[/math]

Операции сложения/вычитания:

[math]\Theta_{\rm k-means}^{d, n} \le knd+ i(kn(2d-1) + knd) = knd+ i(kn(3d-1)) \thicksim O(ikdn)[/math]

Операции умножения/деления:

[math]\Theta_{\rm k-means}^{d, n} \le kd + i(knd + kd) = kd + ikd(n+1) \thicksim O(ikdn) [/math]

Получаем, что временная сложность алгоритма k-means кластеризации [math]n[/math] d-мерных векторов на [math]k[/math] кластеров за [math]i[/math] итераций:

[math] \Theta_{\rm k-means}^{d, n} \thicksim O(ikdn) [/math]

1.7 Информационный граф

Рассмотрим информационный граф алгоритма. Алгоритм k-means начинается с этапа инициализации, после которого следуют итерации, на каждой из которых выполняется два последовательных шага (см. "Схема реализации последовательного алгоритма"):

• распределение векторов по кластерам
• перерасчет центров кластеров

Поскольку основная часть вычислений приходится на шаги итераций, распишем информационные графы данных шагов.

Распределение векторов по кластерам

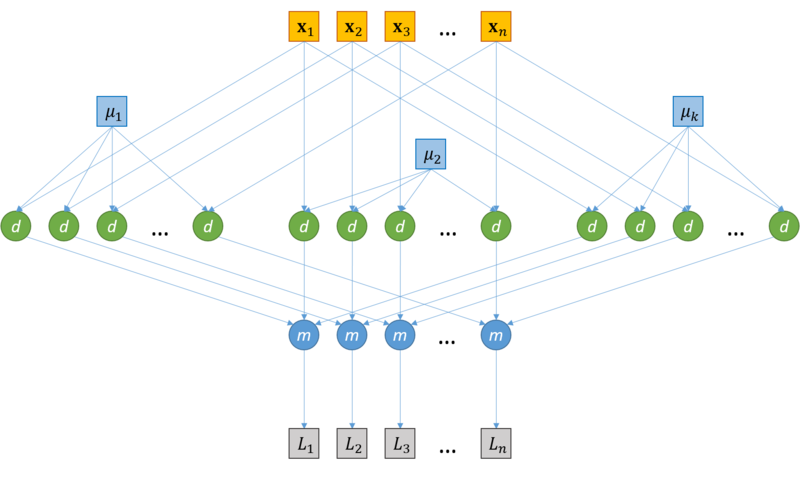
Информационный граф шага распределения векторов по кластерам представлен на рисунке 1. Исходами данного графа является исходные векторы [math]\mathbf{x}_1, ..., \mathbf{x}_n[/math], а также центры кластеров [math]\mathbf{\mu}_1, ... \mathbf{\mu}_k[/math], вычисленные ранее (на шаге инициализации, если рассматривается первая итерация алгоритма, или на шаге пересчета центров кластеров предыдущей итерации в противном случае). Каждая пара векторов данных [math]\mathbf{x}_i, \ i=1,...,n,[/math] и центров кластера [math]\mathbf{\mu}_j, \ j=1,...,k[/math] : ([math]\mathbf{x}_i[/math], [math]\mathbf{\mu}_j[/math]) подаются на независимые узлы "d" вычисления расстояния между векторами (более подробная схема вычисления расстояния представлена далее, рисунок 2). Далее узлы вычисления расстояния "d", соответствующие одному и тому же исходному вектору [math]\mathbf{x}_i[/math] передаются на один узел "m", где далее происходит вычисление новой метки кластера для каждого вектора [math]\mathbf{x}_i[/math] (берется кластер с минимальным результатом вычисления расстояния). На выходе графа выдаются метки кластеров , [math]L_1, ..., L_n[/math], такие что [math]\forall \mathbf{x}_i, \ i=1,...,n, \ \mathbf{x}_i \in S_j \Leftrightarrow L_i = j[/math].

Рис. 1. Схема распределения векторов по кластерам. d – вычисление расстояния между векторами; m – вычисление минимума.

Вычисление расстояния между векторами

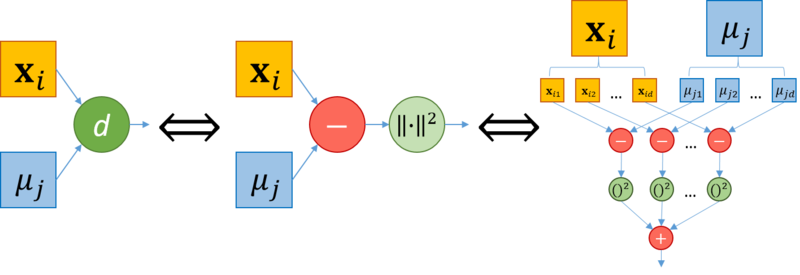
Подробная схема вычисления расстояния между векторами [math]\mathbf{x}_i, \mathbf{\mu}_j[/math] представлена на рисунке 2. Как показано на графе, узел вычисления расстояния между векторами "d" состоит из шага взятия разности между векторами (узел "[math]-[/math]") и взятия нормы получившегося вектора разности (узел "[math]||\cdot||^2[/math]"). Более подробно, вычисление расстояния между векторами [math]\mathbf{x}_i = {x_{i1,}, ...,{x_{in}}}, \mathbf{\mu}_j = {\mu_{j1}, ...,\mu_{jn}}[/math] может быть представлено как вычисление разности между каждой парой компонент [math](x_{iz}, \mu_{jz}), \ z=1,...,d[/math] (узел "[math]-[/math]"), далее возведение в квадрат для каждого узла "[math]-[/math]" (узел "[math]()^2[/math]") и суммирования выходов всех узлов "[math]()^2[/math]" (узел "[math]+[/math]").

Рис. 2. Схема вычисления расстояния между вектором и центром кластера.

Пересчет центров кластеров

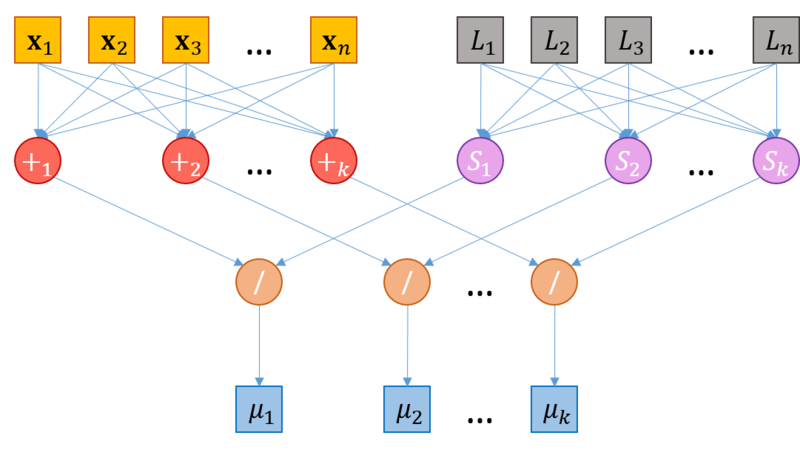
Информационный граф шага пересчета центров кластеров представлен на рисунке 3. Исходами данного графа является исходные векторы [math]\mathbf{x}_1, ..., \mathbf{x}_n[/math], а также им соответствующие метки кластера, [math]L_1, ..., L_n[/math], такие что [math]\forall x_i, \ i=1,...,n, \ \mathbf{x}_i \in S_j \Leftrightarrow L_i = j[/math], вычисленные на этапе распределения векторов по кластерам. Все векторы [math]\mathbf{x}_1, ..., \mathbf{x}_n[/math] подаются в узлы [math]+_1, ...+_k[/math], каждый узел [math]+_m, \ m = 1,...,k,[/math] соответствует операции сложения векторов кластера с номером [math]m[/math]. Метки кластера [math]L_1, ..., L_n[/math] также совместно передаются на узлы [math]S_m, \ m=1,...,k[/math], на каждом из которых вычисляется количество векторов в соответствующем кластере (количество меток с соответствующим значением). Далее каждая пара выходов узлов [math]+_m[/math] и [math]S_m[/math] подается на узел "[math]/[/math]", где производится деление суммы векторов кластера на количество элементов в нем. Значения, вычисленные на узлах "[math]/[/math]", присваиваются новым центрам кластеров (выходные значения графа).

Рис. 3. Схема пересчета центров кластеров

1.8 Ресурс параллелизма алгоритма

Работа алгоритма состоит из [math]i[/math] итераций, в каждой из которых происходит распределение [math]d[/math]-мерных векторов по [math]k[/math] кластерам, а также пересчет центров кластеров в [math]d[/math]-мерном пространстве. В шаге распределения [math]d[/math]-мерных векторов по [math]k[/math] кластерам расстояния между вектором и центрами кластеров вычисляются независимо (отсутствуют информационные зависимости). Центры масс кластеров также пересчитываются независимо друг от друга. Таким образом, имеет место массовый параллелизм. Вычислим параллельную сложность [math]\Psi_*[/math] каждого из шагов, а также параллельную сложность всего алгоритма, [math]\Psi_{\rm k-means}[/math]. Будем исходить из предположения, что может быть использовано любое необходимое число потоков.

Распределение [math]d[/math]-мерных векторов по [math]k[/math] кластерам

Поскольку на данном шаге для каждой пары векторов [math]\mathbf{x}_i, \ i=1,...,n[/math] и [math]\mathbf{\mu}_j, \ j=1,...,k,[/math] операции вычисления расстояния не зависят друг от друга, они могут выполняться параллельно. Тогда, разделив все вычисление расстояний на [math]n[/math] потоков, получим, что в каждом потоке будет выполняться только одна операция вычисления расстояния между векторами размерности [math]d[/math]. При этом каждому вычислительному потоку передаются координаты центров всех кластеров [math]\mathbf{\mu}_1, ..., \mathbf{\mu}_k[/math]. Таким образом, параллельная сложность данного шага определяется сложностью параллельной операции вычисления расстояния между [math]d[/math]-мерными векторами, [math]\Psi_{\rm distance}^d[/math] и сложностью определения наиболее близкого кластера (паралельное взятие минимума по расстояниям), [math]\Psi_{\rm min}^k[/math]. Для оценки [math]\Psi_{\rm distance}^d[/math] воспользуемся параллельной реализацией нахождения частичной суммы элементов массива путем сдваивания. Аналогично, [math]\Psi_{\rm min}^k = \log(k)[/math]. В результате, [math]\Psi_{\rm distance}^d = O(\log(d))[/math]. Таким образом:

[math]\Psi_{\rm distribute}^{k, d} = \Psi_{\rm distance}^d + \Psi_{\rm min}^k = O(\log(d))+O(\log(k)) = O(\log(kd))[/math]

Пересчет центров кластеров в d-мерном пространстве

Поскольку на данном шаге для каждого из [math]k[/math] кластеров центр масс может быть вычислен независимо, данные операции могут быть выполнены в отдельных потоках. Таким образом, параллельная сложность данного шага, [math]\Psi_{\rm recenter}^{k, d}[/math], будет определяться параллельной сложностью вычисления одного центра масс кластера размера [math]m[/math], [math]\Psi_{\rm recenter}^{k, d}[/math], а так как [math]m \le n \Rightarrow \Psi_{\rm recenter}^{d, m} \le \Psi_{\rm recenter}^{d, n}[/math]. Сложность вычисления центра масс кластера [math]d[/math]-мерных векторов размера n аналогично предыдущим вычислениям равна [math]O(\log(n))[/math]. Тогда:

[math]\Psi_{\rm recenter}^{k, d} \le \Psi_{\rm recenter}^{d, n} = O(\log(n))[/math]

Общая параллельная сложность алгоритма

На каждой итерации необходимо обновление центров кластеров, которые будут использованы на следующей итерации. Таким образом, итерационный процесс выполняется последовательно. Тогда, поскольку сложность каждой итерации определяется [math]\Psi_{\rm distribute}^{k, d}[/math] и [math]\Psi_{\rm recenter}[/math], сложность всего алгоритма, [math]\Psi_{\rm k-means}[/math] в предположении, что было сделано [math]i[/math] операций определяется выражением

[math]\Psi_{\rm k-means} \approx i \cdot (\Psi_{\rm distribute}^{k, d} + \Psi_{\rm recenter}^{k, d}) \le i \cdot O(\log(kdn))[/math]

1.9 Входные и выходные данные алгоритма

Входные данные

• Матрица из [math]n \cdot d[/math] элементов [math]x_{i, j} \in \mathbb{R}, \ i=1,...,n, \ j=1,...,d,[/math] – координат векторов (наблюдений).
• Целое положительное число [math]k, \ k \le n[/math] – количество кластеров.

Объем входных данных
[math]1[/math] целое число + [math]n \cdot d[/math] вещественных чисел (при условии, что координаты – вещественные числа).

Выходные данные
[math]n[/math] целых положительных чисел [math]L_1, ..., L_n[/math]– номера кластеров, соотвествующие каждому вектору (при условии, что нумерация кластеров начинается с [math]1[/math]).

Объем выходных данных
[math]n[/math] целых положительных чисел.

1.10 Свойства алгоритма

Вычислительная мощность

Вычислительная мощность алгоритма k-means равна [math]\frac{ikdn}{nd} = ki [/math], где [math]k[/math] – число кластеров, [math]i[/math] – число итераций алгоритма.

Детерминированность и Устойчивость

Алгоритм k-means является итерационным. Количество итераций алгоритма в общем случае не фиксируется и зависит от начального расположения объектов в пространстве, параметра [math]k[/math], а также от начального приближения центров кластеров, [math]\mu_1, ..., \mu_k[/math]. В результате этого может варьироваться результат работы алгоритма. При неудачном выборе начальных параметров итерационный процесс может сойтись к локальному оптимуму. По этим причинам алгоритм не является ни детермирированным, ни устойчивым.

Соотношение последовательной и параллельной сложности алгоритма

[math]\frac{\Theta_{\rm k-means}}{\Psi_{\rm k-means}} = \frac{O(ikdn)}{O(i \cdot \log(kdn))}[/math]

Сильные стороны алгоритма:

• Сравнительно высокая эффективность при простоте реализации
• Высокое качество кластеризации
• Возможность распараллеливания
• Существование множества модификаций

Недостатки алгоритма:

• Количество кластеров является параметром алгоритма

• Чувствительность к начальным условиям

  Инициализация центров кластеров в значительной степени влияет на результат кластеризации.

• Чувствительность к выбросам и шумам

  Выбросы, далекие от центров настоящих кластеров, все равно учитываются при вычислении их центров.

• Возможность сходимости к локальному оптимуму

  Итеративный подход не дает гарантии сходимости к оптимальному решению.

• Использование понятия "среднего"

  Алгоритм неприменим к данным, для которых не определено понятие "среднего", например, категориальным данным.

2 Программная реализация алгоритма

2.4 Выводы для классов архитектур

В однопоточном режиме на наборах данных, представляющих практический интерес (порядка нескольких десятков тысяч векторов и выше), время работы алгоритма неприемлемо велико. Благодаря свойству массового параллелизма должно наблюдаться значительное ускорение алгоритма на многоядерных архитектурах (Intel Xeon), а также на графических процессорах, даже на мобильных вычислительных системах (ноутбуках), оснащенных видеокартой. Алгоритм k-means также будет демонстрировать значительное ускорение на сверхмощных вычислительных комплексах (суперкомпьютерах, системах облачных вычислений).

На сегодняшний день существует множество реализаций алгоритма k-means, в частности, направленных на оптимизацию параллельной работы на различных архитектурах. Предлагается множество адаптаций алгоритма под конкретные архитектуры. Например, авторы работы производят перерасчет центров кластеров на этапе распределения векторов по кластерам.