Библиотека алгоритмов

Материал из Алговики
Перейти к навигации Перейти к поиску

Содержание

1 УМНОЖЕНИЕ МАТРИЦЫ НА ВЕКТОР

XY projection
1.1 Ссылка на описание в энциклопедии AlgoWiki:

Умножение плотной неособенной матрицы на вектор

1.2 Реализация алгоритма на Си:

for(int i = 0; i < size; i++)

for(int j = 0; j < size ; j++)
vec_out[i] += matrix[i][j] * vec _in[j];
1.3 Описание алгоритма на Algolang:

<algo>

<params>
<param name="n" type="int" value="5"></param>
<param name="m" type="int" value="4"></param>
</params>

<block dims="2">
<arg name="i" val="1..m"></arg>
<arg name="j" val="1..n+1"></arg>
<vertex condition="j>1" type="2">
<in src="i,j-1"></in>
</vertex>
</block>

</algo>

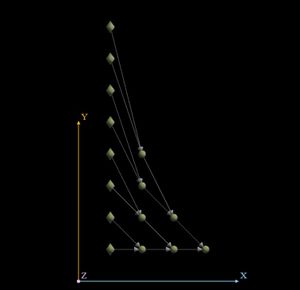
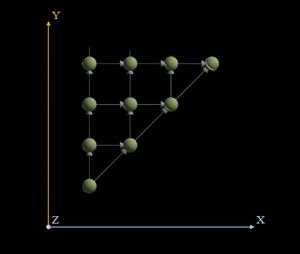
1.4 Характеристики алгоритма (Для умножения матрицы размером m строк на n столбцов на вектор порядка n):
  • Общее количество вершин: m*n+m
  • Длина критического пути: n
  • Каноническая ширина ЯПФ: m

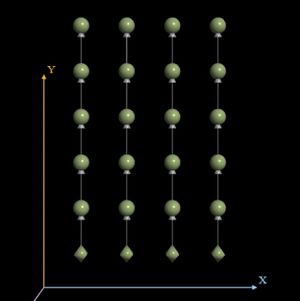
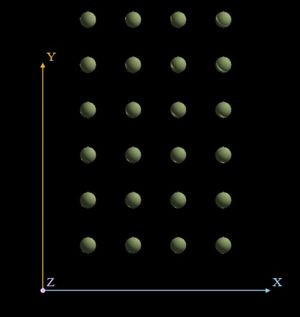
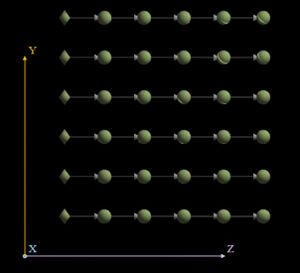
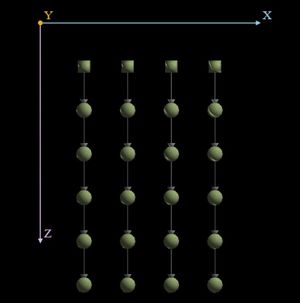
На рисунках представлен результат для матрицы размером 4*5 и вектора длины 5

2 ПЕРЕМНОЖЕНИЕ МАТРИЦ

XY projection
YZ projection
XZ projection
2.1 Ссылка на описание в энциклопедии AlgoWiki:

Перемножение плотных неособенных матриц

2.2 Реализация алгоритма на Си:

for ( int i=0; i<size_1_str;i++)

for (int j=0; j<size_2_col;j++)
{
matrix_out[i][j]=0;
for(int k=0; k<size_common;k++)
matrix_out[i][j]+=matrix_1[i][k]*matrix_2[k][j];
}
2.3 Описание алгоритма на Algolang:

<algo>

<params>
<param name="m" type="int" value="4"></param>
<param name="n" type="int" value="5"></param>
<param name="l" type="int" value="6"></param>
</params>

<block id="1" dims="3">
<arg name="i" val="1..m"></arg>
<arg name="j" val="1..l"></arg>
<arg name="k" val="1..n+1"></arg>
<vertex condition="k>1" type="3">
<in src="i,j,k-1"></in>
</vertex>
</block>

</algo>

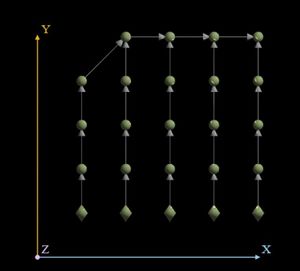
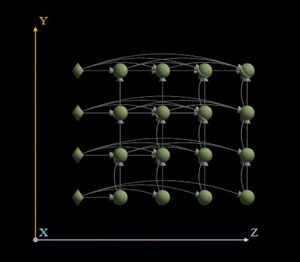
2.4 Характеристики алгоритма (Для умножения матрицы размером m строк на n столбцов на матрицу размером n строк на l столбцов):
  • Общее количество вершин: m*n*l
  • Длина критического пути: n
  • Каноническая ширина ЯПФ: m*l

На рисунках представлено изображение графа алгоритма выходных данных для случая перемножения двух квадратных матриц порядка 4*5 и 5*6











3 НАХОЖДЕНИЕ СУММЫ ЭЛЕМЕНТОВ МАССИВА СДВАИВАНИЕМ

XY projection
3.1 Ссылка на описание в энциклопедии AlgoWiki:

Нахождение суммы элементов массива сдваиванием

3.2 Реализация алгоритма на Си:

for(int i=1;i<=h;i++)

for(int j=0;j<arr_size;j++)
if(j<(arr_size/(pow(2,i))))
arr[j]=arr[j*2]+arr[2*j+1];
3.3 Описание алгоритма на Algolang:

<algo>

<params>
<param name="n" type="int" value="8"></param>
</params>

<block dims="2">
<arg name="i" val="1..((2)log(n)+1)"></arg>
<arg name="j" val="1..n"></arg>
<vertex condition="(i>1)and(j<=(n/(2^(i-1))))" type="1">
<in src="i-1,j*2-1"></in>
<in src="i-1,j*2"></in>
</vertex>
</block>

</algo>

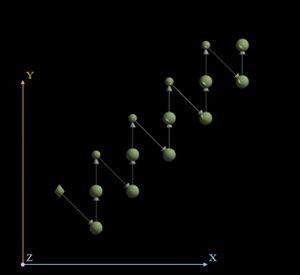
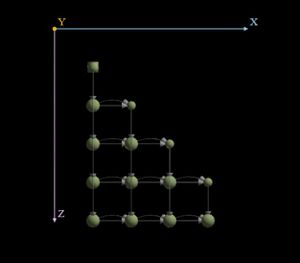
3.4 Характеристики алгоритма (для суммирования массива порядка n):
  • Общее количество вершин: n-1
  • Длина критического пути: [Log2n]
  • Каноническая ширина ЯПФ: n

На рисунке изображён граф алгоритма. В данном случае выполнено суммирование 8 элементов массива. Вершины, соответствующие входным данным, обозначены октаэдром.

4 ПОСЛЕДОВАТЕЛЬНО-ПАРАЛЛЕЛЬНЫЙ МЕТОД СУММИРОВАНИЯ

XY projection
4.1 Ссылка на описание в энциклопедии AlgoWiki:

Последовательно-параллельный метод суммирования

4.2 Описание алгоритма на Algolang:

<algo>

<params>
<param name="n" type="int" value="25"></param>
<param name="p" type="int" value="5"></param>
</params>

<block id="0" dims="2">
количество процессоров
<arg name="i" val="1..p"></arg>
на каждый процессор, кроме одного, распределяется одинаковое количество
элементов массива (n/p, округленное в бОльшую сторону)
<arg name="j" val="1..n"></arg>
<arg name="j" val="1..ceil(n/p)"></arg>

сумма элементов массива, равномерно распределенных по (p-1) процессорам
<vertex condition="(j>1)and(i>1)and(j<ceil(n/p))" type="1">
<in src="i,j-1"></in>
</vertex>

сумма оставшихся эелементов
<vertex condition="(j>1)and(i=1)and(j<=(n-p-(ceil(n/p)-1)*(p-1)))" type="1">
<in src="i,j-1"></in>
</vertex>

последовательное суммирование получившихся сумм на одном из процессоров
<vertex condition="(i>2)and(j=ceil(n/p))" type="1">
<in src="i-1,j"></in>
<in src="i,j-1"></in>
</vertex>
<vertex condition="(i=2)and(j=ceil(n/p))" type="1">
<in src="i-1,n-p-(ceil(n/p)-1)*(p-1)"></in></in>
<in src="i,j-1"></in>
</vertex>
</block>

</algo>

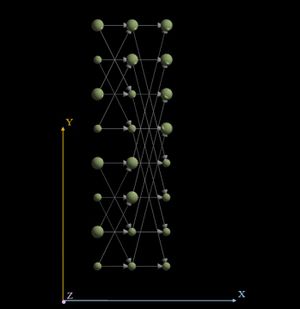
4.3 Характеристики алгоритма (Для суммирования массива порядка n):
  • Общее количество вершин: n-1
  • Длина критического пути:
    • ceil(n/p)-1 - суммирования по частям массива (p ветвей)
    • p-1 - одна последовательная ветвь
  • Каноническая ширина ЯПФ: p

На рисунке изображён граф алгоритма без входных и выходных данных для случая суммирования 25 элементов массива на 5 процессорах.

5 Компактная схема метода Гаусса для трёхдиагональной матрицы

XY projection
5.1 Ссылка на описание в энциклопедии AlgoWiki:

Компактная схема метода Гаусса для трёхдиагональной матрицы

5.2 Описание алгоритма на Algolang:

<algo>

<params>
<param name="n" type="int" value="6"></param>
</params>

<block id="0" dims="2">
<arg name="j" val="1..n"></arg>
<arg name="i" val="1..n"></arg>

деление
<vertex condition="(i=j+1)and(j>1)" type="1">
<in src="j,j"></in>
</vertex>

вычетание
<vertex condition="(j=i)and(j>1)" type="2">
<in src="j,i-1"></in>
</vertex>

умножение
<vertex condition="j=i+1" type="3">
<in src="j-1,i+1"></in>
</vertex>
</block>

</algo>

5.3 Характеристики алгоритма (Для матрицы с рангом n):
  • Общее количество вершин: 3n-3
  • Длина критического пути:
    • n−1 ярусов делений
    • n−1 ярусов умножений
    • n−1 ярусов сложений (вычитаний)
  • Каноническая ширина ЯПФ: 1

На рисунке изображён граф алгоритма для n=6.

6 Простой алгоритм Кули-Тьюки быстрого преобразования Фурье для степеней двойки

XY projection
6.1 Ссылка на описание в энциклопедии AlgoWiki:

Простой алгоритм Кули-Тьюки быстрого преобразования Фурье для степеней двойки

6.2 Описание алгоритма на Algolang:

<algo>

<params>
<param name = "N" type = "int" value = "3"></param>
</params>

<block id="0" dims="2">
<arg name = "I" val = "1..N"></arg>
<arg name = "J" val = "1..2^N"></arg>

<vertex condition = "(J - 1) % (2^I) < 2^(I - 1)" type = "1">
<in src = "I - 1, J"></in>
<in src = "I - 1, J + 2^(I -1)"></in>
</vertex>

<vertex condition = "(J - 1) % (2^I) >= 2^(I - 1)" type = "2">
<in src = "I - 1, J"></in>
<in src = "I - 1, J - 2^(I - 1)"></in>
</vertex>

</block>

</algo>

6.3 Характеристики алгоритма (Для вектора с размерностью n):
  • Общее количество вершин: n*log2n
  • Длина критического пути:
    • log2n операций комплексного сложения/вычитания
    • log2n операций комплексного умножения
  • Каноническая ширина ЯПФ: n

На рисунке изображён граф алгоритма для n=8.

7 Метод Гивенса (вращений) QR-разложения квадратной матрицы

XY projection
YZ projection
XZ projection
7.1 Ссылка на описание в энциклопедии AlgoWiki:

Простой алгоритм Метод Гивенса (вращений) QR-разложения квадратной матрицы (вещественный точечный вариант)

7.2 Описание алгоритма на Algolang:

<algo>

<params>
<param name="n" type="int" value="5"></param>
</params>
<block dims="3">
<arg name="k" val="1..n-1"></arg>
<arg name="i" val="1..n-1"></arg>
<arg name="j" val="1..n"></arg>
выполнение поворота 2-мерного вектора 1 яруса
<vertex condition="(j>k)and(i=k)and(k=1)" type="2">
<in src="k,i,k"></in>
</vertex>
выполнение поворота 2-мерного вектора 1 яруса
<vertex condition="(j>k)and(i>k)and(k=1)" type="2">
<in src="k,i,k"></in>
<in src="k,i-1,j"></in>
</vertex>
выполнение поворота 2-мерного вектора остальных ярусов
<vertex condition="(j>k)and(k>1)and(i=k)" type="2">
<in src="k,i,k"></in>
<in src="k-1,i,j"></in>
<in src="k-1,i-1,j"></in>
</vertex>
операция вычисления параметров поворота остальных ярусов
<vertex condition="(j=k)and(k>1)and(i=k)" type="1">
<in src="k-1,i,j"></in>
<in src="k-1,i-1,j"></in>
</vertex>
выполнение поворота 2-мерного вектора остальных ярусов
<vertex condition="(j>k)and(k>1)and(i>k)" type="2">
<in src="k,i,k"></in>
<in src="k-1,i,j"></in>
<in src="k,i-1,j"></in>
</vertex>
операция вычисления параметров поворота остальных ярусов
<vertex condition="(j=k)and(k>1)and(i>k)" type="1">
<in src="k-1,i,j"></in>
</vertex>
</block>

</algo>

7.3 Характеристики алгоритма (Для матрицы порядка n):
  • Общее количество вершин: n3/3
  • Длина критического пути:
    • 2n−3 макровершины вычисления параметров поворота
    • n−1 макровершин поворотов
  • Каноническая ширина ЯПФ: n

На рисунке изображён Граф алгоритма без отображения входных и выходных данных для n=5.

Источник — https://algowiki-project.org/w/ru/index.php?title=Библиотека_алгоритмов&oldid=28597