Встречная прогонка, точечный вариант
| Встречная прогонка для трёхдиагональной матрицы, точечный вариант | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]8n-2[/math] |
| Объём входных данных | [math]4n-2[/math] |
| Объём выходных данных | [math]n[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]2.5n-1[/math] |
| Ширина ярусно-параллельной формы | [math]4[/math] |
Основные авторы описания: А.В.Фролов.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Описание ресурса параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Встречная прогонка - один из вариантов метода исключения неизвестных в приложении к решению СЛАУ[1][2] вида [math]Ax = b[/math], где
- [math] A = \begin{bmatrix} a_{11} & a_{12} & 0 & \cdots & \cdots & 0 \\ a_{21} & a_{22} & a_{23}& \cdots & \cdots & 0 \\ 0 & a_{32} & a_{33} & \cdots & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & a_{n-1 n-2} & a_{n-1 n-1} & a_{n-1 n} \\ 0 & \cdots & \cdots & 0 & a_{n n-1} & a_{n n} \\ \end{bmatrix}, x = \begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \\ \end{bmatrix}, b = \begin{bmatrix} b_{1} \\ b_{2} \\ \vdots \\ b_{n} \\ \end{bmatrix} [/math]
Часто, однако, при изложении сути методов решения трёхдиагональных СЛАУ[3] элементы правой части и матрицы системы обозначают и нумеруют по-другому, например СЛАУ может иметь вид ([math]N=n-1[/math])
- [math] A = \begin{bmatrix} c_{0} & -b_{0} & 0 & \cdots & \cdots & 0 \\ -a_{1} & c_{1} & -b_{1} & \cdots & \cdots & 0 \\ 0 & -a_{2} & c_{2} & \cdots & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & -a_{N-1} & c_{N-1} & -b_{N-1} \\ 0 & \cdots & \cdots & 0 & -a_{N} & c_{N} \\ \end{bmatrix}\begin{bmatrix} y_{0} \\ y_{1} \\ \vdots \\ y_{N} \\ \end{bmatrix} = \begin{bmatrix} f_{0} \\ f_{1} \\ \vdots \\ f_{N} \\ \end{bmatrix} [/math]
или, если записывать отдельно по уравнениям, то
[math]c_{0} y_{0} - b_{0} y_{1} = f_{0}[/math],
[math]-a_{i} y_{i-1} + c_{i} y_{i} - b_{i} y_{i+1} = f_{i}, 1 \le i \le N-1[/math],
[math]-a_{N} y_{N-1} + c_{N} y_{N} = f_{N}[/math].
Встречная прогонка, как и классическая монотонная, заключается в исключении из уравнений неизвестных, однако, в отличие от монотонной, в ней исключение ведут одновременно с обоих "краёв" СЛАУ (верхнего и нижнего). В принципе, её можно считать простейшим вариантом метода редукции (при m=1 и встречных направлениях монотонных прогонок).
1.2 Математическое описание алгоритма
[math]m[/math] здесь - номер уравнения, на котором "встречаются" две ветви прямого хода - "сверху" и "снизу".
В приведенных обозначениях во встречной прогонке сначала выполняют её прямой ход - вычисляют коэффициенты
"сверху":
[math]\alpha_{1} = b_{0}/c_{0}[/math],
[math]\beta_{1} = f_{0}/c_{0}, [/math]
[math]\alpha_{i+1} = b_{i}/(c_{i}-a_{i}\alpha_{i}), \quad i = 1, 2, \cdots , m-1[/math],
[math]\beta_{i+1} = (f_{i}+a_{i}\beta_{i})/(c_{i}-a_{i}\alpha_{i}), \quad i = 1, 2, \cdots , m-1. [/math]
и "снизу":
[math]\xi_{N} = a_{N}/c_{N}[/math],
[math]\eta_{N} = f_{N}/c_{N}[/math],
[math]\xi_{i} = a_{i}/(c_{i}-b_{i}\xi_{i+1})[/math], [math]\quad i = N-1, N-2, \cdots , m[/math],
[math]\eta_{i} = (f_{i}+b_{i}\eta_{i+1})/(c_{i}-b_{i}\xi_{i+1})[/math], [math]\quad i = N-1, N-2, \cdots , m. [/math]
после чего вычисляют решение с помощью обратного хода
[math]y_{m} = (\eta_{m}+\xi_{m}\beta_{m})/(1-\xi_{m}\alpha_{m})[/math],
[math]y_{m-1} = (\beta_{m}+\alpha_{m}\eta_{m})/(1-\xi_{m}\alpha_{m})[/math],
[math]y_{i} = \alpha_{i+1} y_{i+1} + \beta_{i+1}, \quad i = m-2, \cdots , 1, 0[/math],
[math]y_{i+1} = \xi_{i+1} y_{i} + \eta_{i+1}, \quad i = m, m+1, \cdots , N-1[/math].
В приводимых обычно[3] формулах встречной прогонки нет формулы для компоненты [math]y_{m-1}[/math], которая вычисляется позже в обратном ходе. Однако это удлиняет критический путь графа как в случае с чётным числом переменных, откладывая вычисление [math]y_{m-1}[/math] на момент, когда уже будет вычислена [math]y_{m}[/math], хотя обе компоненты могут быть вычислены одновременно почти независимо друг от друга, так и в случае с нечётным числом переменных, когда для вычисления на "месте встречи" нужно подождать дополнительно одно вычисление коэффициентов либо "сверху" от него, либо "снизу".
Поэтому в более поздних источниках[4] приводятся формулы, которые более оптимальны для нечётного количества неизвестных. В них старт обратного хода заменяется на формулу (в наших обозначениях)
[math]y_{m} = (f_{m}+b_{m}\eta_{m+1}+a_{m}\beta_{m})/(c_{m}-a_{m}\alpha_{m}-b_{m}\xi_{m+1})[/math]
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма можно, как и в случае классической монотонной прогонки, представить состоящим из двух частей - прямого и обратного хода; однако их ширина вдвое больше, чем в монотонном случае. В прямом ходе ядро составляют две независимые последовательности операций деления, умножения и сложения/вычитания. В обратном ходе в ядре остаются только две независимые последовательности операций умножения и сложения.
1.4 Макроструктура алгоритма
В дополнение к возможности представления макроструктуры алгоритма как совокупности прямого и обратного хода, прямой ход также может быть разложен на две макроединицы - прямой ход правой и левой прогонок, выполняемых "одновременно", т.е., параллельно друг другу, для разных половин СЛАУ. Обратный ход также может быть разложен на две макроединицы - обратный ход правой и левой прогонок, выполняемых "одновременно", т.е., параллельно друг другу, для разных половин СЛАУ.
1.5 Схема реализации последовательного алгоритма
Последовательность исполнения метода следующая:
1. Инициализируется прямой ход:
[math]\alpha_{1} = b_{0}/c_{0}[/math],
[math]\beta_{1} = f_{0}/c_{0}[/math],
[math]\xi_{N} = a_{N}/c_{N}[/math],
[math]\eta_{1} = f_{N}/c_{N}[/math].
2. Последовательно выполняются формулы прямого хода:
[math]\alpha_{i+1} = b_{i}/(c_{i}-a_{i}\alpha_{i})[/math], [math]\quad i = 1, 2, \cdots , m-1[/math],
[math]\beta_{i+1} = (f_{i}+a_{i}\beta_{i})/(c_{i}-a_{i}\alpha_{i})[/math], [math]\quad i = 1, 2, \cdots , m-1[/math],
[math]\xi_{i} = a_{i}/(c_{i}-b_{i}\xi_{i+1})[/math], [math]\quad i = N-1, N-2, \cdots , m[/math],
[math]\eta_{i} = (f_{i}+b_{i}\eta_{i+1})/(c_{i}-b_{i}\xi_{i+1})[/math], [math]\quad i = N-1, N-2, \cdots , m[/math].
3. Инициализируется обратный ход:
[math]y_{m-1} = (\beta_{m}+\alpha_{m}\eta_{m})/(1-\xi_{m}\alpha_{m})[/math],
[math]y_{m} = (\eta_{m}+\xi_{m}\beta_{m})/(1-\xi_{m}\alpha_{m})[/math].
4. Последовательно выполняются формулы обратного хода:
[math]y_{i} = \alpha_{i+1} y_{i+1} + \beta_{i+1}[/math], [math]\quad i = m-1, m-2, \cdots , 1, 0[/math],
[math]y_{i+1} = \xi_{i+1} y_{i} + \eta_{i+1}[/math], [math]\quad i = m, m+1, \cdots , N-1[/math].
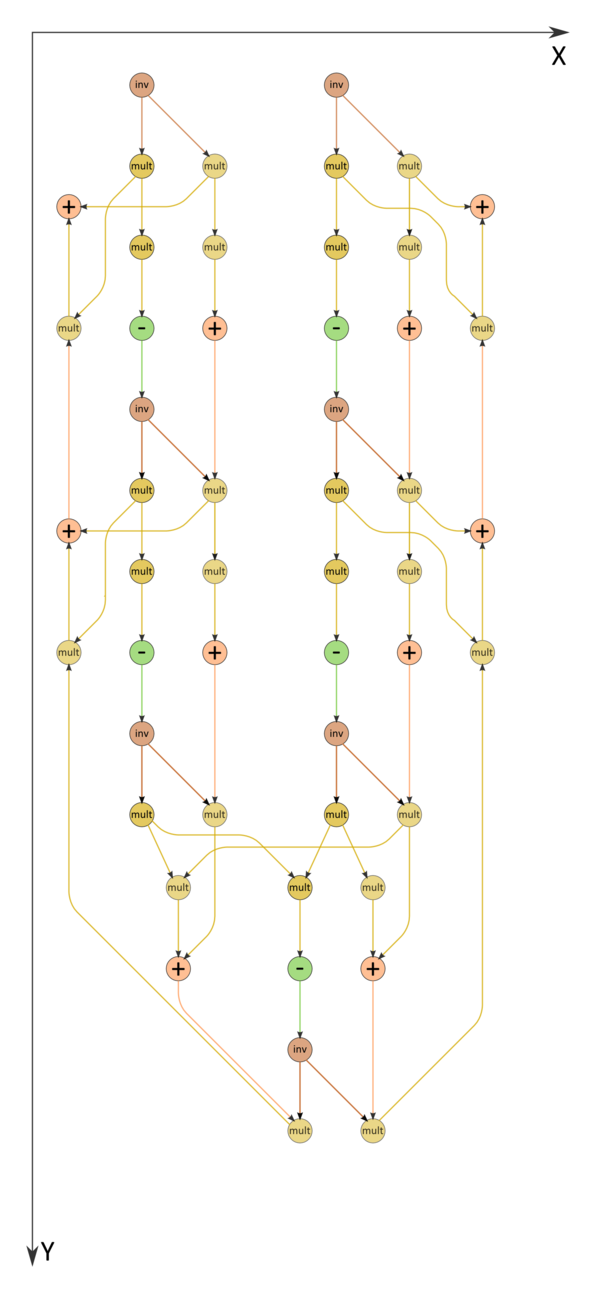
В формулах прямого хода присутствуют пары делений на одно и то же выражение. Их можно заменить вычислением обратных чисел и последующим умножением на эти числа (см. Рисунок 2).
1.6 Последовательная сложность алгоритма
Для выполнения встречной прогонки в трёхдиагональной СЛАУ из n уравнений с n неизвестными в последовательном (наиболее быстром) варианте требуется:
- [math]2n+2[/math] делений,
- [math]3n-2[/math] сложений/вычитаний,
- [math]3n-2[/math] умножений.
Таким образом, при классификации по последовательной сложности встречная прогонка относится к алгоритмам с линейной сложностью.
1.7 Информационный граф
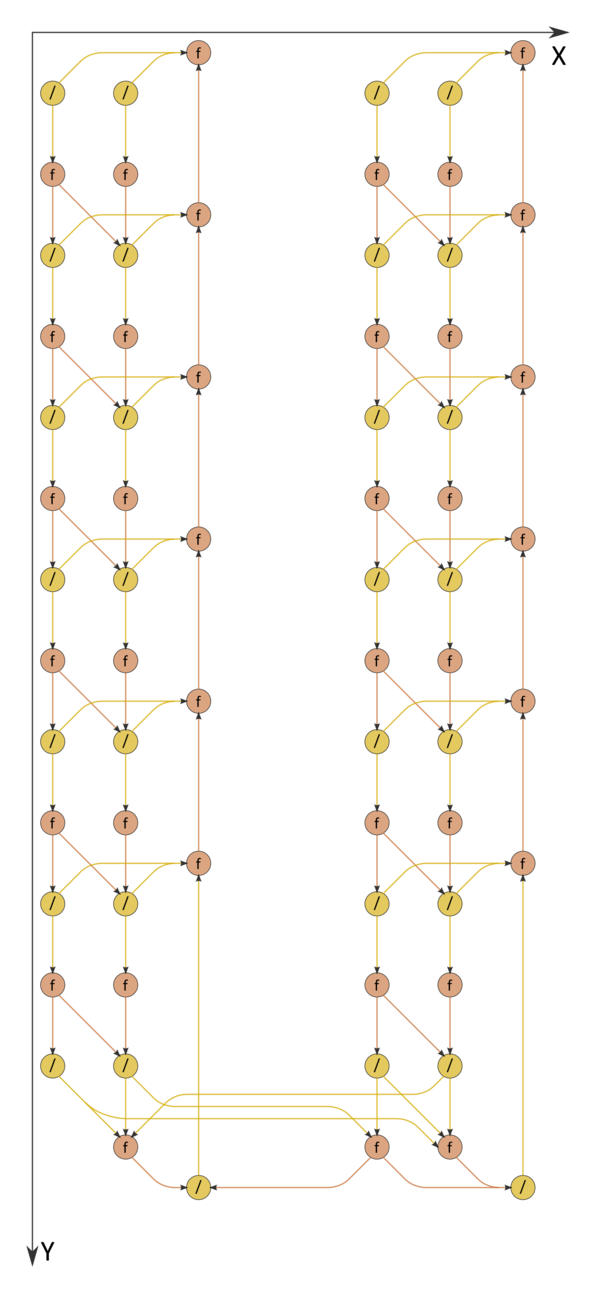
Информационный граф встречной прогонки представлен на рис.1. Как видно, он параллелен на прямом ходе со степенью не более 4, на обратном - со степенью не более 2. При выполнении прямого хода не только сами ветви, но и две подветви каждой из них (левая - разложение матрицы, правая - решение первой из двухдиагональных систем) могут выполняться параллельно друг другу. Правые подветви соответствуют обратному ходу. Из рисунка видно, что не только математическая суть обработки элементов векторов, но даже структура графа алгоритма и направление потоков данных в нём вполне соответствуют названию "обратный ход". Вариант с заменой делений сводится к графу, изображённому на рис.2.
1.8 Описание ресурса параллелизма алгоритма
Обе ветви прямого хода можно выполнять одновременно, если [math]N=2m-1[/math], т.е. [math]n=2m[/math]. В этом случае встречная прогонка требует последовательного выполнения следующих ярусов:
- [math]m+1[/math] ярусов делений (в каждом из ярусов, кроме одного, по 4 деления, в одном - 2 деления),
- по [math]2m-1[/math] ярусов умножений и сложений/вычитаний (в [math]m-1[/math] ярусах - по 4 операции, в [math]m-1[/math] - по две, в одном - три операции).
Таким образом, при классификации по высоте ЯПФ встречная прогонка относится к алгоритмам со сложностью [math]O(n)[/math]. При классификации по ширине ЯПФ сложность этого алгоритма равна [math]4[/math].
При нечётном [math]n[/math] ветви нельзя выполнить синхронно, поэтому предпочтительнее выбирать чётные размеры задач.
1.9 Входные и выходные данные алгоритма
Входные данные: трёхдиагональная матрица [math]A[/math] (элементы [math]a_{ij}[/math]), вектор [math]b[/math] (элементы [math]b_{i}[/math]).
Выходные данные: вектор [math]x[/math] (элементы [math]x_{i}[/math]).
Объём выходных данных: [math]n[/math].
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности, как хорошо видно, является константой (причём менее 4).
При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – тоже константа.
Алгоритм в рамках выбранной версии полностью детерминирован.
Обычно встречная прогонка, как и монотонная, используется для решения СЛАУ с диагональным преобладанием. Тогда гарантируется устойчивость алгоритма. В случае, когда требуется решение нескольких СЛАУ с одной и той же матрицей, ветви вычислений с нахождением коэффициентов можно не повторять. Тогда будет более предпочтителен вариант с заменой делений.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
В зависимости от нужд вычислений, возможны как разные способы хранения матрицы СЛАУ (в виде одного массива с 3 строками или в виде 3 разных массивов), так и разные способы хранения вычисляемых коэффициентов (на месте уже использованных элементов матрицы либо отдельно).
Приведем пример подпрограммы, реализующей встречную прогонку СЛАУ с чётным числом уравнений, где все элементы матрицы хранятся в одном массиве, причём соседние элементы матричной строки размещаются рядом, а вычисляемые коэффициенты - на месте уже ненужных элементов исходной матрицы.
subroutine vprogm (a,x,N) ! N=2m-1
real a(3,0:N), x(0:N)
m=(N+1)/2
a(2,0)=1./a(2,0)
a(2,N)=1./a(2,N)
a(3,0)=-a(3,0)*a(2,0) ! alpha 1
a(1,N)=-a(1,N)*a(2,N) ! xi N
x(0)=x(0)*a(2,0) ! beta 1
x(N)=x(N)*a(2,N) ! eta N
do 10 i=1,m-1
a(2,i)=1./(a(2,i)+a(1,i)*a(2,i-1))
a(2,N-i)=1./(a(2,N-i)+a(3,N-i)*a(2,N-i+1))
a(3,i) = -a(3,i)*a(2,i) ! alpha i+1
a(1,N-i) = -a(1,N-i)*a(2,N-i) ! xi N-i
x(i)=(x(i)-a(1,i)*x(i-1))*a(2,i) ! beta i+1
x(N-i)=(x(N-i)-a(3,N-i)*x(N-i+1))* a(2,N-i) ! eta N-i
10 continue
a(1,0)=1./(1.-a(1,m)*a(3,m-1))
bb=x(m-1)
ee=x(m)
x(m-1)=(bb+a(3,m-1)*ee))*a(1,0) ! y m-1
x(m) = (ee+a(1,m)*bb)*a(1,0) ! y m
do 20 i=m+1,N
x(i)=a(1,i)*x(i-1)+x(i) ! y i
x(N-i)=a(3,N-i)*x(N-i+1)+x(N-i) ! y N-i
20 continue
return
end
Приведем также пример подпрограммы, реализующей встречную прогонку СЛАУ с нечётным числом уравнений, где все элементы матрицы хранятся в одном массиве, причём соседние элементы матричной строки размещаются рядом, а вычисляемые коэффициенты - на месте уже ненужных элементов исходной матрицы.
subroutine vprogm (a,x,N) ! N=2m-1
real a(3,N), x(N)
m=(N+1)/2
a(2,1)=1./a(2,1)
a(2,N)=1./a(2,N)
a(3,1)=-a(3,1)*a(2,1) ! alpha 2
a(1,N)=-a(1,N)*a(2,N) ! xi N
x(1)=x(1)*a(2,1) ! beta 2
x(N)=x(N)*a(2,N) ! eta N
do 10 i=2,m-1
a(2,i)=1./(a(2,i)+a(1,i)*a(2,i-1))
a(2,N+1-i)=1./(a(2,N+1-i)+a(3,N+1-i)*a(2,N+2-i))
a(3,i) = -a(3,i)*a(2,i) ! alpha i+1
a(1,N+1-i) = -a(1,N+1-i)*a(2,N+1-i) ! xi N-i
x(i)=(x(i)-a(1,i)*x(i-1))*a(2,i) ! beta i+1
x(N+1-i)=(x(N+1-i)-a(3,N+1-i)*x(N+2-i))* a(2,N+1-i) ! eta N-i
10 continue
a(2,m)=1./(a(2,m)+a(1,m)*a(2,m-1)+a(3,m)*a(2,m+1))
x(m) =(x(m)-a(1,m)*x(m-1)-a(3,m)*x(m+1))*a(2,m) ! y m
do 20 i=m+1,N
x(i)=a(1,i)*x(i-1)+x(i) ! y i up
x(N+1-i)=a(3,N+1-i)*x(N+2-i)+x(N+1-i) ! y i down
20 continue
return
end
2.2 Возможные способы и особенности параллельной реализации алгоритма
Встречная прогонка задумана изначально для случая, когда нужно найти только какую-то близкую к "середине" компоненту вектора решения, а остальные не нужны (решение т.н. "частичной задачи"). При появлении параллельных компьютерных устройств оказалось, что у встречной прогонки есть небольшой ресурс параллелизма и она убыстряет счёт, если её верхнюю и нижнюю ветви раскидать на 2 процессора. Однако для получения массового параллелизма встречная прогонка непригодна из-за низкой ширины своей ЯПФ (равной 4 на прямом и 2 - на обратном ходе).
Алгоритм встречной прогонки настолько прост, что, в тех случаях, когда он по каким-либо причинам понадобился, большинство использующих его исследователей-прикладников просто пишут соответствующий фрагмент программы самостоятельно. Поэтому встречную прогонку в пакеты программ обычно не включают.
2.3 Результаты прогонов
2.4 Выводы для классов архитектур
Встречная прогонка - метод для архитектуры классического, фон-неймановского типа. Для распараллеливания решения СЛАУ с трёхдиагональной матрицей следует взять какой-либо её параллельный заменитель, например, наиболее распространённую циклическую редукцию или уступающий ей по критическому пути графа, но имеющий более регулярную структуру графа новый последовательно-параллельный метод.
3 Литература
- ↑ Воеводин В.В. Вычислительные основы линейной алгебры. М.: Наука, 1977.
- ↑ Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. М.: Наука, 1984.
- ↑ Перейти обратно: 3,0 3,1 Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений. М.: Наука, 1978.
- ↑ Ильин В.П., Кузнецов Ю.И. Трехдиагональные матрицы и их приложения. М.: Наука. Главная редакция физико-математической литературы, 1985г. ,208 с.