Квадратурные (кубатурные) методы численного интегрирования по отрезку (многомерному кубу)

Основные авторы описания: А.В.Смирнов, А.Б.Кукаркин

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Численное интегрирование — приближенное вычисление значения определенного интеграла. Допустим, нам дана функция [math]f(x)[/math], определенная на отрезке или многомерном кубе, и возможность получать ее численное значение в любой из точек области определения за фиксированное время. Задача — вычислить определенный интеграл данной функции по заданной области и дать оценку погрешности вычисления.

Исторически численное интегрирование также называлось численной квадратурой, а многомерное — кубатурой. Большая советская энциклопедия определяет слово «квадратура» следующим способом (лат. quadratura — придание квадратурной формы). 1) Число квадратных единиц в площади данной фигуры. 2) Построение квадрата, равновеликого данной фигуре. 3) Вычисление площади или интеграла.

В данной статье рассматривается семейство методов численного интегрирования, объединенных общим принципом: область интегрирования разбивается по каждой из осей на равное количество частей. В каждой из полученных маленьких областей интеграл приближается простой функцией (например, линейной), значение которой вычисляется явно (путем вычисления подынтегрального выражения в одной или нескольких точках). Ввиду линейности оператора интегрирования по областям полученные значения суммируются и представляют собой результат интегрирования.

К данному типу относятся одномерные метод прямоугольников, метод трапеций, метод парабол (метод Симпсона), метод Гаусса, метод Гаусса-Кронрода. Часть перечисленных методов обобщается и для многомерного случая. Обобщенно все эти методы называются квадратурными. В многомерном случае они также могут называться кубатурными (это слово не несет нкаких дополнительных смыслов). Также говорится, что перечисленные методы используют квадратурные (кубатурные) формулы.

Подходы, в которых область делится не на равные друг другу отрезки (кубы), называются адаптивными и не рассматриваются к данной статье.

Все перечисленные выше методы, а также подобные им могут быть объединены следующим образом: область интегрирования содержит [math]M[/math] точек, в каждой из которых необходимо вычислить значение подынтегрального выражения и помножить его на весовой коэффициент, затем данные числа складываются, и полученная сумма и представляет собой результат интегрирования.

1.2 Математическое описание алгоритма

Исходные данные: функция [math]f[/math] от [math]n[/math] переменных, границы области интегрирования, представляющей собой многомерный куб (по каждой из осей интегрирования заданы минимальное и максимальное значения координаты), максимальное число [math]M[/math] точек, в которых можно вычислить функцию [math]f[/math].

Вычисляемые данные: число, представляющее собой приближенное значение интеграла и, если это позволяет выбранный метод, число, представляющее собой оценку погрешности. По количеству точек [math]M[/math] и методу интегрирования определяются размеры прямоугольных параллелепипедов, на которые разбивается область интегрирования. В каждом из параллелепипедов в зависимости от выбора метода определяются свои точки для вычисления функции [math]f[/math] и весовые коэффициенты.

Наибольшее разнообразие выбора методов достигается в одномерном случае.

Метод прямоугольников.

Функция для заданного отрезка приближается константной функцией, тем самым интеграл приближается значением функции в одной точке. Обычно в качестве этой точки используется граница отрезка или, лучше, его середина.

[math]\int\limits_a^b f(x)dx\approx f((a+b)/2)*(b-a)[/math]

Метод трапеций.

[math]f(x)[/math] приближается линейной функцией, тем самым интеграл приближается усредненным значением по краям отрезка.

[math]\int\limits_a^b f(x)dx\approx (f(a)+f(b))*(b-a)/2[/math]

Метод парабол (метод Симпсона).

[math]f(x)[/math] приближается параболой, пересекающей график функции на краях отрезка и в его середине.

[math]\int\limits_a^b f(x)dx\approx \frac{b-a}6\left(f(a)+4f\left(\frac{a+b}2\right)+f(b)\right)[/math]

Метод Гаусса.

[math]f(x)[/math] приближается прямой как в методе трапеций, однако в качестве точек выбираются не концы отрезка, что позволяет увеличить точность.

[math]\int\limits_a^b f(x)dx\approx \frac{b-a}2\left(f\left(\frac{a+b}2-\frac{b-a}{2\sqrt 3}\right)+f\left(\frac{a+b}2+\frac{b-a}{2\sqrt 3}\right)\right)[/math]

В двумерной ситуации распространены методы прямоугольников (вычисление в центре квадрата), метод трапеций (в углах квадрата), а также двумерный метод Гаусса. В трехмерной ситуации также можно использовать метод Гаусса, однако для больших размерностей не остается ничего, способного конкурировать с методом прямоугольников.

Так или иначе. на подготовительной стадии определяется [math]M[/math] наборов координат [math]x_{1,i},\ldots,x_{n,i}[/math], где [math]i[/math] меняется от [math]1[/math] до [math]M[/math], в которых будет вычисляться функция [math]f[/math] и набор весовых коэффициентов [math]c_i[/math], на которые будут умножаться значения функции, после чего управление передается вычислительному ядру алгоритма.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро последовательной версии алгоритма представляет собой вычисление суммы

[math]\sum\limits_{i=1}^n c_i f(x_{1,i},\ldots,x_{n,i}).[/math]

В реальных примерах эффективность алгоритма определяется именно эффективностью вычисления функции [math]f(x)[/math], т.к. затраты времени на её вычисление гораздо больше времени на соответствующие операции суммирования и умножения.

1.4 Макроструктура алгоритма

Начальная стадия работы алгоритма заключается в том, что по выбранному методу, координатам, ограничивающим область интегрирования, и максимальному число точек, в которых должно производиться вычисление функции, определяется набор точек для этих вычислений. Время, требуемое на эту операцию, оценивается константой.

1.5 Схема реализации последовательного алгоритма

Формулы для реализации алгоритмы были приведены выше. В цикле обходятся все необходимые точки, и в них происходит вычисление значения функции. Результаты вычисления умножаются на весовые коэффициенты и складываются. При последовательной реализации алгоритма для экономии памяти можно не генерировать сразу весь массив точек, в которых должна быть вычислена функция, а получать их последовательно.

1.6 Последовательная сложность алгоритма

Общее время, затрачиваемое на вычисление функции растет примерно как [math]tM[/math], где [math]t[/math] — время, необходимое на однократное вычислении функции [math]f[/math], а [math]M[/math] — количество точек, в которых вычисляется функция [math]f[/math]. Таким образом, алгоритм является линейным относительно количества точек интегрирования.

1.7 Информационный граф

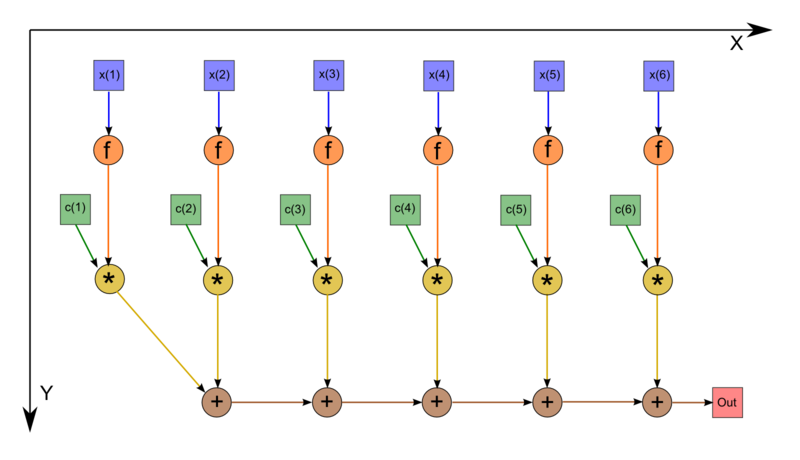
Граф алгоритма интегрирования можно описать аналитически, а также представить его в виде рисунка.

Граф алгоритма состоит из трех групп вершин. Вершины на верхнем ярусе берут в качестве входных данных координаты и вычисляют по ним значение функции [math]f[/math]. Вершины на втором ярусе умножают полученное значение на соответствующий весовой коэффициент. Вершины на третьем ярусе поочередно складывают полученные значения; результат сложения относится к выходным данным.

Рисунок 1. Квадратурные (кубатурные) методы численного интегрирования по отрезку (многомерному кубу)

1.8 Ресурс параллелизма алгоритма

Для вычисления методом кубатур интеграла функции необходимо последовательно выполнить следующие ярусы алгоритма:

• Вычисление исходной функции [math]f[/math], производящееся независимо для различных точек и выполняющееся за близкое к константному время [math]t[/math], эта операция является основной вычислительной часть алгоритма.

• Умножение полученных результатов на соответствующие весовые коэффициенты.

• Сложение полученных результатов.

В общем случае время, затрачиваемое на сложение или умножение пренебрежимо мало по сравнением со временем на вычисление функции [math]f[/math], а все вычисления функции [math]f[/math] могут производиться на различных вычислительных узлах, тем самым, задача вычисления интеграла методом кубатур идеально подходит для параллельной реализации. Однако при значительном увеличении количества узлов (в случае, когда оно становится сравнимым с количеством точек, в которых вычисляется функция), ресурс параллелизма может быть ограничен накладными расходами, такими как передача исходного выражения на каждый из вычислительных узлов.

Таким образом, до тех пор, пока количество вычислительных узлов не превышает количества точек, в которых должно быть произведено интегрирование, алгоритм выполняется за около константное время. Однако, в реальных вычислениях обычно требуется значительно большее количество точек интегрирования (измеряемое миллионами), чем количество вычислительных узлов, которые можно задействовать, и в таком случае сложность алгоритма является линейной. В этом случае алгоритм распараллеливается идеально.

1.9 Входные и выходные данные алгоритма

Входными данными для алгоритма являются размерность [math]n[/math], границы интегрирования (два массива длины [math]n[/math]), ограничение [math]M[/math] на количество точек интегрирования, выбор метода интегрирования и функция [math]f[/math] — подынтегральное выражение. Она обычно задается в виде функции, написанной на используемом языке программирования или же в строковом виде, если реализация алгоритма имеет встроенный аналог компилятора, работающий с используемым классом функций.

К входным данными для вычислительного ядра алгоритма относится функция [math]f[/math] и массив длины [math]M[/math], содержащий точки, в которых должно быть произведено вычисление.

Выходными данными является число - результат интегрирования и, возможно, второе число, представляющее собой оценку погрешности.

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является линейным (отношение линейной сложности к константной). В данной оценке предполагается, что накладные расходы пренебрежимо малы по отношению к вычислению подынтегрального выражения.

При этом сложность ядра алгоритма относительно объема входных данных также является линейной. При лимитированных ресурсах как параллельная реализация, так и последовательная реализация имеют линейную сложность относительно количества точек интегрирования. Однако, константа, представляющая собой отношение затрачиваемого в параллельной и последовательной реализациях времени, может быть весьма значительной и приближаться к количеству доступных узлов.

Алгоритм является почти полностью детерминированным — выбор точек интегрирования полностью определяется выбором метода и ограничением на их количество. Использование иного порядка суммирования конечных результатов может приводить к накоплению ошибок округления, однако обычно его влияние незначительно по сравнению с оценкой ошибки, представляемой алгоритмом. Дуги информационного графа являются полностью локальными.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

В простейшем варианте вычислительное ядро метода на Фортране можно записать следующим образом:

		double::res
		DO  I = 1, M
			double::a = f(x(I))
			res = res + a
		END DO

2.2 Возможные способы и особенности реализации параллельного алгоритма

Самым естественным способом реализации параллельного алгоритма является независимое вычислении функции [math]f[/math] в заданных точках различными вычислительными узлами. Это может быть реализовано как при помощи технологии threads или OpenMP при запуске на одном узле, так и, например, при использовании межпроцессорных обменов при помощи MPI. Головной узел передает остальным вычислительным узлам "определение" функции [math]f[/math], и затем раздает подчиненным узлам точки, в которых должна вычисляться функция. Для оптимизации процесса коммуникации возможно организовать передачу сразу наборов точек.

Представляется также возможным одновременное вычисление нескольких значений функции одним узлом, однако такой подход требует адаптации самого алгоритма вычисления функции [math]f[/math] и не всегда является применимым. Например, использование команд типа AVX для микропроцессоров позволяет выполнять по 4 сложения или умножения за один такт работы процессора, однако так могут складываться лишь последовательно расположенные вещественные числа. Однако использование подобных ускорителей или, скажем, перевод алгоритма на использование графических процессоров, безусловно требует модификации самого алгоритма вычисления функции [math]f[/math] и уточнения класса функций, для которых будет применяться данная реализация.

Существующие библиотеки, осуществляющие интегрирование, обычно не используют алгоритм, описанный в данной статье, в чистом виде. Ввиду того, что функция может быть близкой к константе в части области интегрирования и существенно изменяться в другой части, намного эффективней оказываются так называемые адаптивные алгоритмы, в которых точки для вычисления функции располагаются не равномерно по области интегрирования, а добавляются постепенно на основании предыдущих вычислений. Кроме того, для многомерного интегрирования кубатурные правила становятся зачастую неэффективными, и требуется дробить не каждую ось в отдельности, а распределять точки случайным образом по области интегрирования. Такие подходы имеют относятся к классу методов Монте-Карло.

2.4 Выводы для классов архитектур

Интерес представляет случай, когда алгоритм вычисления функции может быть адаптирован для одновременного вычисления в большом количестве точек. Например, если функция является рациональной, то алгоритм может быть представлен как серия операций сложения, умножения и других операций над массивами чисел. В этом случае возможна реализация, в которой данные операции выполняются на графическом ускорителе GPGPU, что может приводить к существенному ускорению работы алгоритма по сравнению с вычислениями на центральном процессоре.