Последовательно-параллельный метод нахождения всех частных выражений для ассоциативных операций

1 Описание свойств и структуры алгоритма

1.1 Словесное описание алгоритма

1.1.1 Решаемая задача

Пусть у нас на входе есть некоторый массив данных, записанный в вектор $\vec{x}$ размерности $n$. При этом нам на выходе нужно выдать все результаты вычислений частных результатов последовательного выполнения некоторой ассоциативной операции $\circ$, то есть для всех $i$ от $1$ до $n$ вычислить выражения типа

$x_1 \circ x_2 \circ \cdots \circ x_{i - 1} \circ x_i$

Подобная задача возникает во многих случаях: при нахождении частных максимумов, сумм, произведений, при решении двухдиагональных (в т. ч. блочных) систем линейных алгебраических уравнений, при выполнении схемы Горнера и т. п. В каждом конкретном случае у решения задачи последовательно-параллельным методом будут свои особенности, описанные в соответствующем разделе. Здесь же мы опишем алгоритм общего вида. Операцию $\circ$ будем называть «суммирование».

1.1.2 Алгоритм

При использовании последовательно-параллельного метода массив разбивается на $p$ кусков (каждый кусок — на своём «процессоре»), в каждом из которых сначала частные выражения вычисляются обычным последовательным способом, после чего, используя ассоциативность операции, производится «сборка» полных частных выражений.

1.2 Математическое описание

Исходные данные: одномерный массив $n$ чисел.

Вычисляемые данные: $n$ частных выражений, получаемых каждое из некоторого числа начальных элементов массива.

Формулы метода: число $n$ разлагается в выражение типа $n = (p - 1) k + q$, где $p$ — количество процессоров, $k = \lceil \frac{n}{p} \rceil$, $q = n - k (p - 1)$.

После этого на $i$-м процессоре ($i \lt p$) последовательно вычисляется «сумма» (частное выражение для данной ассоциативной операции) элементов массива, начиная с $(i - 1) k + 1$-го, до $i k$-го.

$S_i = \bigcirc_{j = 1}^k x_{k (i - 1) + j}$

На $p$-м процессоре последовательно вычисляется сумма элементов массива, начиная с $(p - 1) k + 1$-го до $(p - 1) k + q$-го.

$S_i = \bigcirc_{j = 1}^q x_{k (p - 1) + j}$

По окончании этого процесса процессоры обмениваются данными и на одном из них получившиеся полные выражения для всех процессоров «суммируются» последовательно друг с другом

$\bigcirc_{i = 1}^p S_i$

а к частным выражениям каждого из процессоров добавляются полные суммы всех предыдущих выражений.

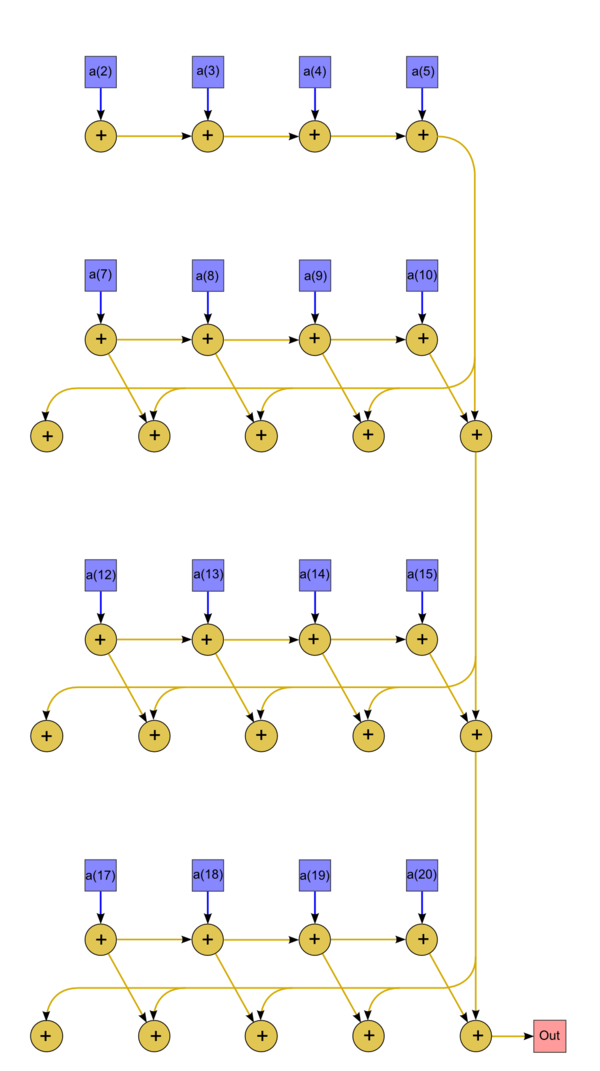
Удобно сразу рассмотреть граф алгоритма, до пункта «Информационный граф», поскольку графическое представление довольно наглядно даёт математику алгоритма. Здесь $'''n = 20'''$. В первом горизонтальном столбце идут вычисления готовых частных результатов для $i$ от 1 до 5 (для 1 он уже готов и равен $x_1$). Во втором — промежуточные частные результаты, где используются элементы от 6-го до 10-го (6-й берётся готовым), в третьем (пока считаем только столбцы, которые используют входные данные) — от 11-го до 15-го (11-й берётся готовым), в четвёртом — от 16-го до 20-го (16-й — готовый). После вычисления в указанных столбцах вычисляются операции в оставшихся столбцах: в первом вычисляются окончательные частные результаты с 6-го по 10-й, во втором — с 11-го по 15-й, в третьем — с 16-го по 20-й.

Последовательно-параллельный метод суммирования с нахождением частных выражений

1.3 Вычислительное ядро алгоритма

Вычислительное ядро последовательно-параллельного метода можно составить из множественных (всего $p$) вычислений «обобщённых сумм» элементов массива:

$S_i = \bigcirc_{j = 1}^k x_{k (i - 1) + j}$

и ещё $n - k$ вычислений частных результатов.

1.4 Макроструктура алгоритма

Как уже записано в описании ядра алгоритма, основную часть метода составляют множественные (всего $p$) вычисления «обобщённых сумм»

$S_i = \bigcirc_{j = 1}^k x_{k (i - 1) + j}$

а также $n - k$ вычислений частных результатов.

1.5 Описание схемы реализации последовательного алгоритма

Формулы метода описаны выше. Последовательность исполнения суммирования может быть разная — как по возрастанию, так и по убыванию индексов. Обычно, однако, этот алгоритм в его последовательном виде не применяют, поскольку в нём присутствует $n - k - p$ избыточных по сравнению с последовательным методом операций.

1.6 Последовательная сложность алгоритма

Для вычисления полной «суммы» массива, состоящего из $n$ элементов, при любых разложениях $n$ суть алгоритма сводится к простому переставлению скобок в формуле «суммирования», и количество операций неизменно и равно $n - 1$. Кроме этого, $n - k - p$ операций выполняется избыточно. Поэтому алгоритм должен быть отнесён к алгоритмам линейной сложности по количеству последовательных операций.

1.7 Информационный граф

Граф алгоритма в виде рисунка изображён выше.

1.8 Описание ресурса параллелизма алгоритма

Для «суммирования» массива порядка n последовательно-параллельным методом в параллельном варианте требуется последовательно выполнить следующие ярусы:

• $k - 1$ ярусов «суммирования» по частям массива ($p$ ветвей),
• $p - 1$ ярусов «суммирования» ($k$ ветвей).

Таким образом, в параллельном варианте критический путь алгоритма (и соответствующая ему высота ЯПФ) будет зависеть от произведённого разбиения массива на части. В оптимальном случае ($p = k = \sqrt{n}$) высота ЯПФ будет равна $2 \sqrt{n} - 2$.

При классификации по высоте ЯПФ, таким образом, последовательно-параллельный метод относится к алгоритмам со сложностью корень квадратный. При классификации по ширине ЯПФ его сложность будет такой же — корень квадратный.

1.9 Описание входных и выходных данных

Входные данные: массив $\vec{x}$ (элементы $x_i$).

Дополнительные ограничения: отсутствуют.

Объём входных данных: $n$.

Выходные данные: $n$ частных «сумм» элементов массива.

Объём выходных данных: $n$.

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является корнем квадратным (отношение линейной к корню квадратному). При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных — всего-навсего 1 (входных и выходных данных столько же, сколько операций). При этом алгоритм не вполне полностью детерминирован, суммирование может быть проведено в разном порядке. Использование другого порядка выполнения ассоциативных операций может дать, с учётом особенностей входных данных, уменьшение влияния ошибок округления на результат. Дуги информационного графа частично локальны (в случае нелокальности имеют место пучки рассылочных дуг).

2 Программная реализация

В простейшем (без перестановок суммирования) варианте на Фортране можно записать так:

	DO  I = 1, P
		SUM (K*(I-1)+1) = X(K*(I-1)+1)
		IF (I.LQ.P) THEN
			DO J = 2,K
				SUM(K*(I-1)+J)=SUM(K*(I-1)+J-1)+X(K*(I-1)+J)
		             END DO
		ELSE
			DO J = 2,Q
				SUM(K*(I-1)+J)=SUM(K*(I-1)+J-1)+X(K*(I-1)+J)
		             END DO
		END IF
	END DO
	DO I = 2,P
		IF (I.LQ.P) THEN
			DO J = 1,K
				SUM(K*(I-1)+J)=SUM(K*(I-1)+J)+SUM(K*(I-1))
		             END DO
		ELSE
			DO J = 1,Q
				SUM(K*(I-1)+J)=SUM(K*(I-1)+J)+SUM(K*(I-1))
		             END DO
		END IF
	END DO

Можно записать и аналогичные схемы, где суммирование будет проводиться в обратном порядке. Подчеркнём, что граф алгоритма обеих схем - один и тот же!

2.7 Существующие реализации алгоритма

В чистом виде алгоритм последовательно-параллельного метода встречается редко, чаще ему предпочитают схему сдваивания. В последовательном варианте из-за избыточности вычислений его вообще почти не применяют.