Применение методов Монте-Карло для оценки опционов европейского типа

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Методы Монте-Карло можно определить как численные методы решения задач при помощи моделирования случайных величин. Эти методы находят широкое применение в различных областях, в частности, в финансовой математике, например, их можно применить для определения цены опциона европейского типа.

Рассмотрим эволюционирующий в непрерывном времени финансовый рынок, состоящий из двух типов активов: акции (рисковые активы, S) и облигации (безрисковые активы, B). Для моделирования рынка будем использовать модель Блэка–Шоулса. Данная модель после ряда преобразований представляет собой систему стохастических дифференциальных уравнений следующего вида:

[math]dB_t = rB_tdt, B_0 \gt 0, (1)[/math]

[math]dS_t = S_t((r-\delta)dt - \sigma dW_t), S_0 \gt 0. (2)[/math]

Здесь первое уравнение представляет собой обыкновенное дифференциальное уравнение, описывающее поведение цены облигации [math]B_t[/math], на изменение которой влияет процентная ставка [math]r[/math]. Уравнение (2) является стохастическим дифференциальным уравнением, описывающим эволюцию цены акции [math]S_t[/math]. В этом уравнении: [math]\sigma[/math] - волатильность акции, [math]\delta[/math] - ставка дивиденда, [math]W_t[/math] - винеровский случайный процесс.

Сделаем несколько предположений касательно рынка:

1. пусть модель будет без дивидендов: [math]\delta = 0[/math];

2. процентные ставки постоянны;

3. если время измеряется в годах, то все рассмотренные процентные ставки участвуют в уравнениях как числа от 0 до 1 и выражают проценты годовых, измеренные в долях.

При этих предположениях рассмотренная система имеет аналитическое решение:

[math]S_t = S_0 e^{(r - \sigma^2/2)t + \sigma W_t}[/math].

Опцион, как производный финансовый инструмент, представляет собой контракт между сторонами [math]P_1[/math] и [math]P_2[/math], который дает право стороне [math]P_2[/math] в некоторый момент времени [math]t[/math] в будущем купить у стороны [math]P_1[/math] или продать стороне [math]P_1[/math] акции по зафиксированной в контракте цене [math]K[/math]. За это право сторона [math]P_2[/math] выплачивает фиксированную сумму (премию) [math]C[/math] стороне [math]P_1[/math]. При этом K называется ценой исполнения опциона (страйк, strike price), а [math]C[/math] – ценой опциона.

Основная идея заключения контракта состоит в игре двух лиц – [math]P_1[/math] и [math]P_2[/math]. Вторая сторона выплачивает некоторую сумму [math]C[/math] и в некоторый момент времени [math]T[/math] (срок выплаты, зафиксированный в контракте) принимает решение: покупать акции по цене [math]K[/math] у первой стороны или нет. Решение принимается в зависимости от соотношения цены [math]S_T[/math] и [math]K[/math]. Если [math]S_T \lt K[/math], покупать акции не выгодно, сторона [math]P_1[/math] получила прибыль [math]C[/math], а [math]P_2[/math] – убыток [math]C[/math]. В случае, если [math]S_T \gt K[/math], сторона [math]P_2[/math] покупает у первой акции по цене [math]K[/math], в ряде случаев получая прибыль.

Справедливая цена опциона – цена, при которой наблюдается баланс выигрыша/проигрыша каждой из сторон. Определяется она как средний выигрыш стороны [math]P_2[/math]:

[math]C = \mathop{\mathbb{E}}(e^{-rT} max\{S_T - K, 0\})[/math].

Точное решение этой системы уравнений известно:

[math]C = S_0N(d_1) - Ke^{-rT}N(d_2),[/math]

[math]d_1 = ln{\frac{S_0}{K}} + \frac{(r + \sigma^2 / 2)T}{\sigma\sqrt{T}},[/math]

[math]d_2 = d_1 - \sigma\sqrt{T}.[/math]

Особенность точного решения заключается в том, что оно может оказаться недействительным в ряде случаев, например, при переменных процентных ставках. В этом случае система уравнений [math](1),(2)[/math] обычно интегрируется численно.

1.2 Математическое описание алгоритма

Решаемая задача имеет следующий вид:

[math]C = e^{-rT}\int^{+\infty}_{-\infty}{f(z)\varphi(z)dz}, (3)[/math]

[math]f(z) = max\{S_0 e^{(r - \sigma^2/2)T + \sigma\sqrt{T}z} - K, 0\}, (4)[/math]

[math]\varphi(z) = \frac{1}{\sqrt{2\pi}} e^{-z^2/2}.[/math]

Для вычисления этого интеграла будем использовать метод Монте-Карло. Если мы рассмотрим случайную величину [math]X = f(z)[/math], то математическое ожидание этой случайной величины будет совпадать с формулой (3) с точностью до коэффициента дисконтирования. Формула для вычисления искомого интеграла имеет вид:

[math]\hat{C} = \frac{e^{-rT}}{N} \sum^{N}_{i=1}{f(z_i)},[/math]

[math]f(z_i) = max\{S_0 e^{(r - \sigma^2/2)T + \sigma\sqrt{T}z} - K, 0\}, z_i \sim N_{0,1}.[/math]

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма составляет вычисление следующей суммы:

[math]\sum^{N}_{i=1}{f(z_i)}.[/math]

Поскольку время, требуемое на операцию сложения в реальных примерах мало по сравнению с временем, затрачиваемом на вычисление функции [math]f(z_i)[/math], для производительности вычислений становится маловажным, каким конкретным образом осуществлять сложение и умножение.

1.4 Макроструктура алгоритма

Алгоритм представляет собой сумму значений функции от случайной величины.

1.5 Схема последовательной реализации алгоритма

Формулы для реализации алгоритма приведены выше [math](1)[/math]. С помощью генератора случайных чисел в цикле получаются точки, и в них вычисляется соответствующая функция. Результаты складываются, полученная сумма умножается на коэффициент. При последовательной реализации для экономии памяти можно сразу не генерировать массив всех точек, в которых должна быть вычислена функция, а получать их последовательно.

1.6 Последовательная сложность алгоритма

Время, затраченное на вычисление интеграла растет как [math]Nt[/math], где [math]N[/math] – количество случайных точек, [math]t[/math] – время, необходимое для вычисления функции.

1.7 Информационный граф алгоритма

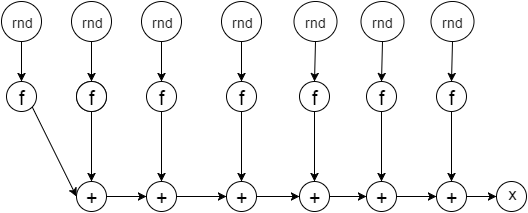
Информационный граф алгоритма представлен на рисунке 1,

Рисунок 1 – Информационный граф алгоритма

где вершина [math]f[/math] – вычисление функции [math]f(z)[/math], [math]rnd[/math] – генерация случайного числа. Анализ этого графа производится в последующих разделах описания алгоритма.

1.8 Ресурс параллелизма алгоритма

Для вычисления интеграла [math](3)[/math] методом Монте-Карло требуется последовательно выполнить следующие ярусы:

1) вычисление случайного числа [math]z[/math],

2) вычисление функции [math]f[/math] на основании полученного случайного числа,

3) сложение полученных результатов.

В общем случае, все вычисления функции [math]f[/math] могут производиться на разных узлах, следовательно, алгоритм идеально поддается распараллеливанию. При классификации по высоте ярусно-параллельной формы этот алгоритм имеет сложность 3. При классификации по ширине – [math]O(N)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные для вычисления алгоритма: число точек [math]N[/math], волатильность акции [math]\sigma[/math], время жизни опциона [math]T[/math], страйк [math]K[/math], процентная ставка [math]r[/math], стоимость акции в начальный момент времени [math]S_0[/math]. Выходные данные: справедливая цена опциона [math]C[/math].

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложностей в случае неограниченных ресурсов является линейным.

При этом сложность ядра алгоритма относительно объема входных данных также является линейной. При лимитированных ресурсах как параллельная реализация, так и последовательная реализация имеют линейную сложность относительно количества точек интегрирования. Однако, константа, представляющая собой отношение затрачиваемого в параллельной и последовательной реализациях времени, может быть весьма значительной и приближаться к количеству доступных узлов. Таким образом, ускорение должно быть близко к линейному.

2 Программная реализация алгоритма

2.1 Особенности последовательной реализации алгоритма

Код последовательной реализации на языке C может выглядеть так:

    double price(int N, double sigma, double T, double K, double S0, double r) {
	coeff = exp(-r*T) / N, result = .0, sigma_coeff = (r - sigma * sigma / 2) * T, sigma_T_coeff = sigma * sqrt(T);
	for (int i = 0; i < N; i++) {
	    result += max(0, S0 * exp(sigma_coeff + sigma_T_coeff * normalrand(i)) - K);
	}
	return coeff * result;
    }

Представленный алгоритм не является полностью детерминированным, так как он основан на использовании последовательностей случайных чисел.

2.2 Локальность данных и вычислений

Данные в представленном алгоритме обладают хорошей локальностью, так как на каждом шаге алгоритма приходится использовать значения переменных sigma_coeff и sigma_T_coeff, что повышает вероятность попадания этих значений в кэш.

2.3 Возможные способы и особенности реализации параллельного алгоритма

Один из возможных вариантов реализации алгоритма – независимое вычисление значений функции [math]f(z)[/math] на различных вычислительных узлах, например, с помощью технологии MPI. «Подводным камнем» такой реализации может стать генерация случайных чисел, которая должна быть независимой на каждом вычислительном узле. Желательно использовать генератор случайных чисел с достаточно большим периодом.

2.4 Масштабируемость алгоритма и его реализации

Теоретические оценки показывают, что алгоритм должен быть хорошо масштабируем.

2.6 Выводы для классов архитектур

При достаточно большом числе точек N возможна реализация алгоритма на GPU для достижения большей скорости выполнения, чем на обычных процессорах.

2.7 Существующие реализации

Есть открытая реализация методов Монте-Карло, являющаяся частью GSL (GNU Scientific Library). Данная библиотека включает в себя как классический алгоритм, так и два адаптивных: «Vegas» и «Miser».

Реализация алгоритма доступна тут: [1], в многокарточном варианте - тут: [2]