Простой алгоритм Кули-Тьюки быстрого преобразования Фурье для степеней двойки

Простой алгоритм Кули-Тьюки
Последовательный алгоритм
Последовательная сложность	[math]O (n log_{2} n)[/math]
Объём входных данных	[math]n[/math]
Объём выходных данных	[math]n[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O (log_{2} n)[/math]
Ширина ярусно-параллельной формы	[math]n[/math]

Основные авторы описания: А.В.Фролов.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Простой алгоритм Кули-Тьюки - один из вариантов быстрого преобразования Фурье для комплексных векторов с размерностью, равной степени двойки, без использования специфичных приёмов, использующихся для степеней четвёрки, восьмёрки и др. Заключается в последовательном применении метода быстрого преобразования Фурье и сведении преобразования к последовательности преобразований Фурье размерности 2 и выполнения умножений на т.н. поворотные множители. Несмотря на то, что проигрывает алгоритмам Кули-Тьюки, разлагающим степени двойки на степени 4, 8 и др. и использующим их специфику, весьма распространён, что связано с самой простой из алгоритмов БПФ записью программной реализации.

1.2 Математическое описание алгоритма

Исходные данные: преобразуемый комплексный вектор [math]a[/math] (элементы [math]a_{i}[/math]).

Вычисляемые данные: комплексный вектор - результат преобразования [math]b[/math] (элементы [math]b_{i}[/math]).

Размерность векторов - [math]n[/math], причём [math]n = 2^l[/math]

1.2.1 Рекурсивное описание

Вектор записывается по строкам по 2 элемента в каждой. После этого над каждой строкой выполняется преобразование Фурье порядка 2, получившиеся элементы умножаются на поворотные множители [math]exp (2 \pi i(m-1)(j-1)/n)[/math] ([math]m[/math] - номер строки, [math]j[/math] - номер столбца), после чего выполняется БПФ порядка [math]n/2[/math] над каждым из столбцов. Поскольку для 1-го столбца поворотные множители равны 1, то реально умножение на них не выполняется, а умножения на поворотные множители элементов второго столбца соединяются с преобразованием Фурье порядка 2. Эта комбинация, называемая "бабочкой" в среде специалистов по БПФ, и является основной операцией в простом алгоритме Кули-Тьюки. "Бабочка" состоит из вычисления суммы двух комплексных чисел, а также из вычисления их разности с последующим умножением на комплексное число. Всего на каждом шаге выполняется [math]n/2[/math] "бабочек", а шагов - [math]l-1[/math]. Последний, [math]l[/math]-й шаг вычисляет только суммы и разности.

1.2.2 Тригонометрические функции

Несмотря на то, что в вычислениях используются поворотные множители [math]exp (2 \pi i(m-1)(j-1)/n)[/math], нецелесообразно вычислять их в процессе выполнения алгоритма Кули-Тьюки, поскольку вычисления косинусов и синусов (в мнимой экспоненте) тогда составили бы львиную долю вычислений алгоритма. Поэтому обычно (как и в других версиях БПФ) поворотные множители вычисляются заранее и хранятся в специальном массиве. Здесь мы будем предполагать, что алгоритм выполняется именно так.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма составляют "бабочки", состоящие из вычисления суммы двух комплексных чисел, а также из вычисления их разности с последующим умножением на комплексное число. Всего их [math](1/2) n log_{2} n [/math] штук, при этом в [math]n/2[/math] из них умножение не выполняется.

1.4 Макроструктура алгоритма

Макроструктура алгоритма лучше всего описывается рекурсивно, как [math]n/2[/math] преобразований Фурье порядка 2, умножение [math]n/2[/math] пар комплексных чисел и затем 2 БПФ порядка [math]n/2[/math].

1.5 Схема реализации последовательного алгоритма

Нерекурсивная схема организации состоит в том, что на каждом шаге (а всего их [math]log_{2} n [/math]) для выполнения "бабочки" все элементы разбиваются на [math]n/2[/math] пар. В зависимости от номера шага, разница координат для каждой пары элементов удваивается. На первом шагу она равна 1, на последнем - [math]n/2[/math]. При этом результат суммы записывается в элемент с меньшим номером, а результат вычитания с последующим умножением - в элемент с большим.

1.6 Последовательная сложность алгоритма

Если считать только главные члены выражений для последовательной сложности алгоритма, то простой алгоритм Кули-Тьюки может быть выполнен за [math]n log_{2} n[/math] операций комплексного сложения и [math](1/2) n log_{2} n [/math]операций комплексного умножения. Таким образом, простой алгоритм Кули-Тьюки может быть отнесён к линейно-логарифмическому классу по последовательной сложности.

1.7 Информационный граф

Рисунок 1. Простой алгоритм Кули-Тьюки для n=8. Op+ - операция сложения двух комплексных чисел. Op- - операция вычитания двух комплексных чисел и умножения результата вычитания на комплексное число (поворотный множитель). В последнем столбце операций умножение не производится. Привязка вершин выполнена по оси абсцисс - к параметру внешнего цикла, по оси ординат - к обрабатываемым элементам массива

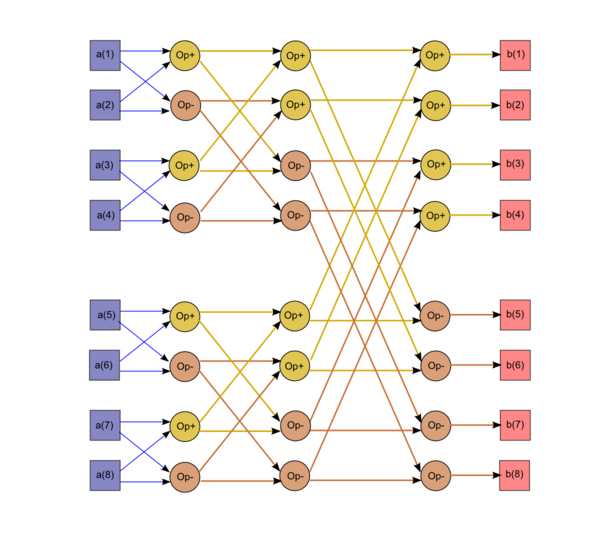
Как видно из рисунка, этот граф не является линейным ни по размерам, ни по формулам для дуг графа. По размерам он линейно-логарифмический, а формулы дуг имеют экспоненциальные компоненты.В элементарной "бабочке" на i-м шаге каждый раз участвует пара элементов массива, у которых запись их номеров, уменьшенных на единицу, в двоичной системе различается только в i-1-м бите.

1.8 Ресурс параллелизма алгоритма

Если считать только главные члены выражений, то простой алгоритм Кули-Тьюки имеет критический путь, состоящий из [math]log_{2} n [/math] операций комплексного сложения/вычитания и [math]log_{2} n [/math] операций комплексного умножения. Таким образом, простой алгоритм Кули-Тьюки может быть отнесён к логарифмическому классу по параллельной сложности. По ширине ЯПФ сложность алгоритма линейна.

1.9 Входные и выходные данные алгоритма

Входные данные: вектор [math]a[/math] (элементы [math]a_{i}[/math]).

Объём входных данных: [math]n[/math] .

Выходные данные: вектор [math]b[/math] (элементы [math]b_{i}[/math]).

Объём выходных данных: [math]n[/math].

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является линейным.

При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – логарифмическая.

При этом алгоритм полностью детерминирован.

Заметим, что простой алгоритм Кули-Тьюки не является оптимальным даже для векторов размером степень двойки. Однако здесь мы не рассматриваем другие алгоритмы БПФ.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

В простейшем варианте алгоритм на Фортране можно записать так, что входной и выходной массивы совпадают (здесь использован массив X):

         
        subroutine STEP2(x,y,pov)
        complex x, y, pov, u, v
        u = x + y
        v = (x-y)*pov
        x = u
        y = v
        return
        end
        subroutine FFT2(X, POV, N, N2, L)
C
C L = Log2N
C N2 = N/2
C
        complex X(0:N-1), POV(0:N2-1)
        DO I = 0, L-1
            DO J = 0, N2/2**I-1
            DO K = 0, 2**I-1
                call STEP2(X(2*J*2**I+K)), X(2*J*2**I+2**I+K), POV(J*2**I))
            END DO
            END DO
         END DO
         return
         end

Здесь предполагается, что поворотные множители первого шага (они потом используются и на последующих шагах) предвычислены заранее и лежат в элементах массива POV (а в его нулевом элементе - единица). К сожалению, подавляющее большинство реализаций простого алгоритма Кули-Тьюки вычисляет поворотные множители одновременно с вычислением "бабочки", что её значительно замедляет.

2.2 Возможные способы и особенности параллельной реализации алгоритма

Простой алгоритм Кули-Тьюки быстрого преобразования Фурье для степеней двойки весьма распространён среди начинающих, использующих БПФ, и его сравнительно легко можно найти в Интернете с помощью поисковых сайтов. Как правило, эти реализации не используют описанных выше приёмов улучшения эффективности вычислений - ни для последовательной, ни для параллельной архитектуры. Связано это с тем, что сам по себе простой алгоритм Кули-Тьюки быстрого преобразования Фурье для степеней двойки проигрывает другим алгоритмам Кули-Тьюки, которые используют специфику, например, чётных степеней двойки, и потому более экономичны. Поэтому большинство исследователей, которым нужны более быстрые программы БПФ, не улучшают эффективность этого алгоритма, а меняют его на другой. Это же рекомендуем делать и читателям.

2.4 Выводы для классов архитектур

Граф простого алгоритма Кули-Тьюки лучше всего из коммуникационных сетей отображается на сеть типа гиперкуб. Распространённость БПФ в методах решения различных задач поэтому привела к популярности идеи вычислительных систем с сетью типа гиперкуб в начале развития различных параллельных вычислительных систем. В настоящее время, однако, массово такие вычислительные системы не используются по физическим причинам, делающим гиперкуб большой размерности труднореализуемым на практике. Как видно из графа, при простом его разбиении на части прямыми, параллельными оси шагов, на первых шагах алгоритма обмены между разными частями будут отсутствовать, но, начиная с некоторого момента, они станут составлять величину, сопоставимую с количеством арифметических операций. Этого, однако, можно избежать, если примерно посередине алгоритма переупорядочить все данные. В графе это будет соответствовать смене разбиения на части. При выполнении указанных рекомендаций, алгоритм можно будет реализовать более эффективно, чем в настоящее время, и на архитектурах типа кластерной и на других архитектурах, реализующих разбиение процесса на независимые ветви.