Равномерная норма вектора, вещественная версия, последовательно-параллельный вариант

Основные авторы описания: А.В.Фролов.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Равномерная норма вектора используется в качестве одной из базовых операций в широком круге методов — как для вычисления получаемой ошибки финальных результатов, так и для промежуточных вычислений.

1.2 Математическое описание алгоритма

Исходные данные: одномерный массив [math]n[/math] чисел.

Вычисляемые данные: максимум абсолютной величины элементов массива.

Формулы метода: для вектора [math]\vec{a}[/math] из [math]n[/math] элементов вычисляется выражение [math]\max\limits_i |a_i|[/math].

При этом в последовательно-параллельном варианте используется последовательный порядок сравнения элементов (обычно от меньших индексов к большим) по частям массива, после чего последовательным методом выбирается максимум из полученных максимумов этих частей.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро вычисления равномерной нормы в последовательно-параллельном варианте можно представить в виде параллельного набора вычислений равномерных норм в последовательном варианте и одного финального вычисления равномерной нормы в последовательном варианте.

1.4 Макроструктура алгоритма

Как уже записано в описании ядра алгоритма, основную часть вычисления равномерной нормы в последовательном варианте составляет выполнение последовательного выбора максимума из модулей частей массива, и затем выполнение последовательного выбора максимума из уже вычисленных максимумов.

1.5 Схема реализации последовательного алгоритма

Формулы метода описаны выше. Последовательность исполнения может быть разная - как по возрастанию, так и по убыванию индексов в соответствующих частях массива. Обычно без особых причин порядок не меняют, используя естественный (возрастание индексов).

1.6 Последовательная сложность алгоритма

Для вычисления равномерной нормы массива, состоящего из [math]N[/math] элементов, количество операций вычисления модуля неизменно и равно [math]N[/math], а количество операций вычисления максимума равно [math]N-1[/math]. Поэтому алгоритм должен быть отнесён к алгоритмам линейной сложности по количеству последовательных операций.

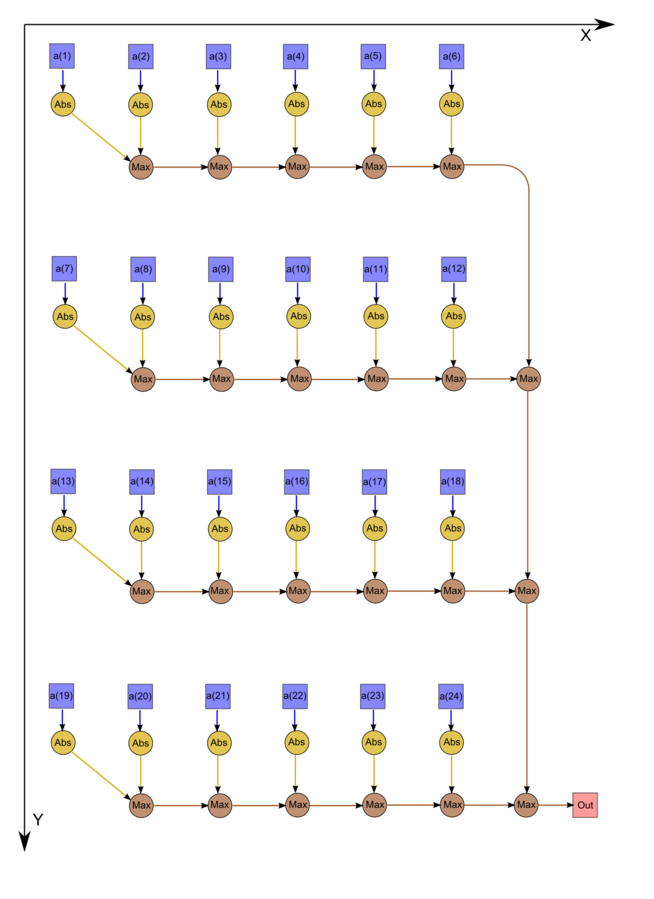
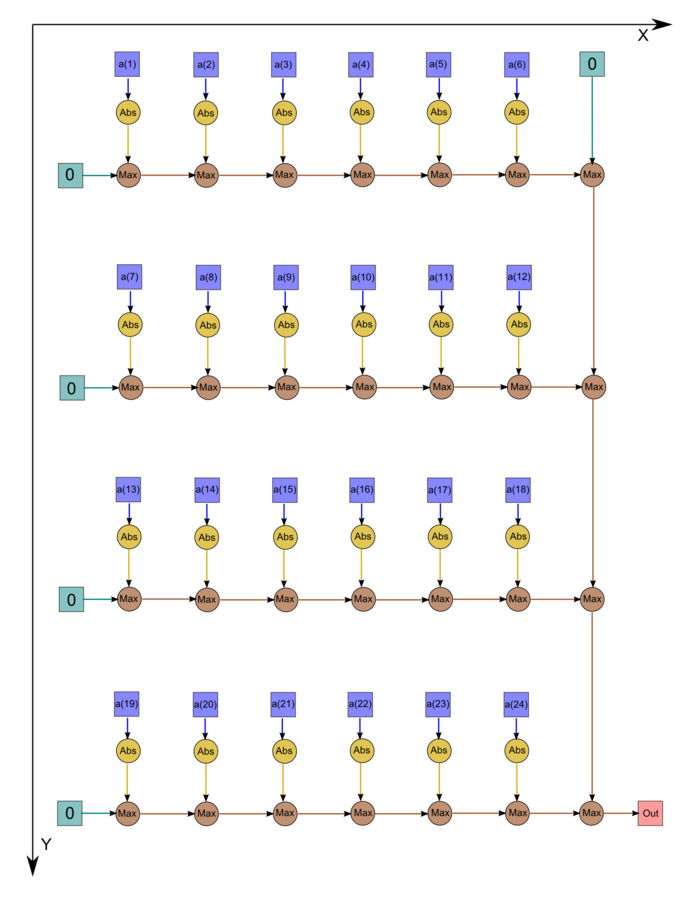
1.7 Информационный граф

На рис.1 изображён граф алгоритма граф для случая [math]n = 24[/math]. Однако следует отметить, что в большинстве случаев программисты не экономят на одном вызове функции максимума, а инициализируют начальное значение переменной нулём. В этом случае граф становится таким, как на рис.2 ([math]n = 24[/math]).

• 

  Рисунок 1. Вычисление равномерной нормы с экономией вызовов функции максимума

• 

  Рисунок 2. Вычисление равномерной нормы без экономии вызовов функции максимума]

1.8 Ресурс параллелизма алгоритма

Последовательно-параллельный вариант вычисления равномерной нормы массива (в более экономном варианте) можно представить составленным из трёх частей. В первой из них выполняется [math]N[/math] вычислений абсолютной величины в одном параллельном ярусе. Во второй части параллельно выполняется [math]p[/math] ветвей [math]N / p - 1[/math] длиной, выбирающих максимальные из частей массива. И, наконец, в третьей части последовательно, длиной [math]p - 1[/math], выбирается максимум из максимумов. Таким образом, в получившемся алгоритме высота параллельной формы будет равна 1 операции вычисления функции ABS плюс [math]N / p + p - 2[/math] операций выбора максимума. Минимум будет достигнут при [math]p = \sqrt{N}[/math] и будет равен [math]2 \sqrt{N} - 2[/math] максимумов плюс одно вычисление абсолютной величины. В таком виде алгоритм должен быть отнесён к алгоритмам сложности порядка «корня квадратного» по высоте. По ширине параллельной формы он за счёт отбрасывания знаков будет линеен, но можно, увеличив вдвое высоту, тоже сделать его сложности порядка «корня квадратного».

1.9 Входные и выходные данные алгоритма

Входные данные: массив [math]a[/math] (элементы [math]a_i[/math]).

Дополнительные ограничения: отсутствуют.

Объём входных данных: [math]n[/math].

Выходные данные: максимум модулей элементов массива.

Объём выходных данных: один скаляр.

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является корнем квадратным из размера. При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных — всего-навсего 1 (входных и выходных данных почти столько же, сколько операций; если точнее — даже больше на 2). При этом алгоритм полностью детерминирован. Дуги информационного графа локальны. Важной особенностью алгоритма является то, что его видоизменение и переход к другому графу (например, способу разбиения [math]N[/math] на множители) никак не повлияет на ошибки округления результата, поскольку функция максимума, в отличие от базовой арифметики (сложения и умножения) остаётся ассоциативной и в условиях действия машинного округления.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

В простейшем (входные данные — вектор, [math]p = \sqrt{N}[/math]) варианте на Фортране можно записать так:

	NORMX = ABS(A(1))
	DO J = 2, P
		NORMX = MAX( NORMX, ABS(A(J)))
	END DO
	DO I = 1, P-1
		NORMY = ABS (A(P*I+1))
		DO J = 2,P
			NORMY = MAX (NORMY, ABS (A(P*I+J)))
		END DO
		NORMX = MAX (NORMX, NORMY)
	END DO

В варианте с «холостым» выбором максимума запись такая:

	NORMX = 0.
	DO J = 1, P
		NORMX = MAX( NORMX, ABS(A(J)))
	END DO
	DO I = 1, P-1
		NORMY = 0.
		DO J = 1,P
			NORMY = MAX (NORMY, ABS (A(P*I+J)))
		END DO
		NORMX = MAX (NORMX, NORMY)
	END DO

2.2 Возможные способы и особенности параллельной реализации алгоритма

Помимо выписанных выше простейших реализаций, существуют более сложные коды, реализующие тот же алгоритм. В основном он применяется для вычисления равномерных норм полей вычисляемых данных, которые изначально двумерны, трёхмерны и т. п. Для вычисления норм одномерных векторов в стандартных библиотеках применяется более простой последовательный метод.