Сдвиг аргументов многочлена по схеме Горнера, вещественная версия, последовательный вариант

1 Описание свойств и структуры алгоритма

1.1 Словесное описание алгоритма

1.1.1 Решаемая задача

Для данного многочлена

$P_n(x) = a_0 x^n + a_1 x^{n - 1} + \dots + a_{n - 1} x + a_n$

с данного скаляра $\alpha$ нужно выписать этот же многочлен по степеням $x - \alpha$, то есть представить его в виде

$P_n(x) = b_0 (x - \alpha)^n + b_1 (x - \alpha)^{n - 1} + \dots + b_{n - 1} (x - \alpha) + b_n$

1.1.2 Общая схема

Решение задачи с помощью схемы Горнера состоит в последовательном применении её и вычисления коэффициентов.

1.2 Математическое описание

Исходные данные: одномерный массив $n + 1$ чисел $a_k$ и скаляр $\alpha$.

Вычисляемые данные: одномерный массив $n + 1$ чисел $b_k$.

Формулы метода: из теоремы Безу и соотношения

$P_n(x) = (x - \alpha) Q_{n - 1}(x)+P_n(\alpha)$

видно, что $b_n = P_n(\alpha)$. Разделив многочлен на $x - \alpha$ по схеме Горнера, мы находим последний искомый коэффициент, а также видим, что остальная часть равна $(x - \alpha) Q_{n - 1}(x)$. Поэтому достаточно применять схему Горнера к многочленам-«частным», чтобы получить в конце все искомые коэффициенты.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро сдвига аргументов многочлена по схеме Горнера в последовательном варианте можно представить как в качестве последовательного применения $n$ схем Горнера с уменьшающимся порядком, так и в качестве набора $\frac{n (n + 1)}{2}$ «двойных» операций (умножение элементов получаемого массива на один и тот же скаляр и добавление результата к следующему элементу входного массива).

1.4 Макроструктура алгоритма

Как уже записано в описании ядра алгоритма, основную часть сдвига аргументов многочлена по схеме Горнера в последовательном варианте можно представить как в качестве последовательного применения $n$ схем Горнера с уменьшающимся порядком, так и в качестве набора $\frac{n (n + 1)}{2}$ «двойных» операций (умножение элементов получаемого массива на один и тот же скаляр и добавление результата к следующему элементу входного массива).

1.5 Описание схемы реализации последовательного алгоритма

Схема метода описана выше. Последовательность исполнения - по возрастанию индексов, с укорачиванием внутреннего цикла. Простейшая программа приведена в разделе «Особенности реализации последовательного алгоритма».

1.6 Последовательная сложность алгоритма

Для вычисления сдвига аргументов многочлена по схеме Горнера для многочлена степени $n$, количество операций умножения равно количеству операций сложения и равно $\frac{n (n + 1)}{2}$. Поэтому алгоритм должен быть отнесён к алгоритмам квадратичной сложности по количеству последовательных операций.

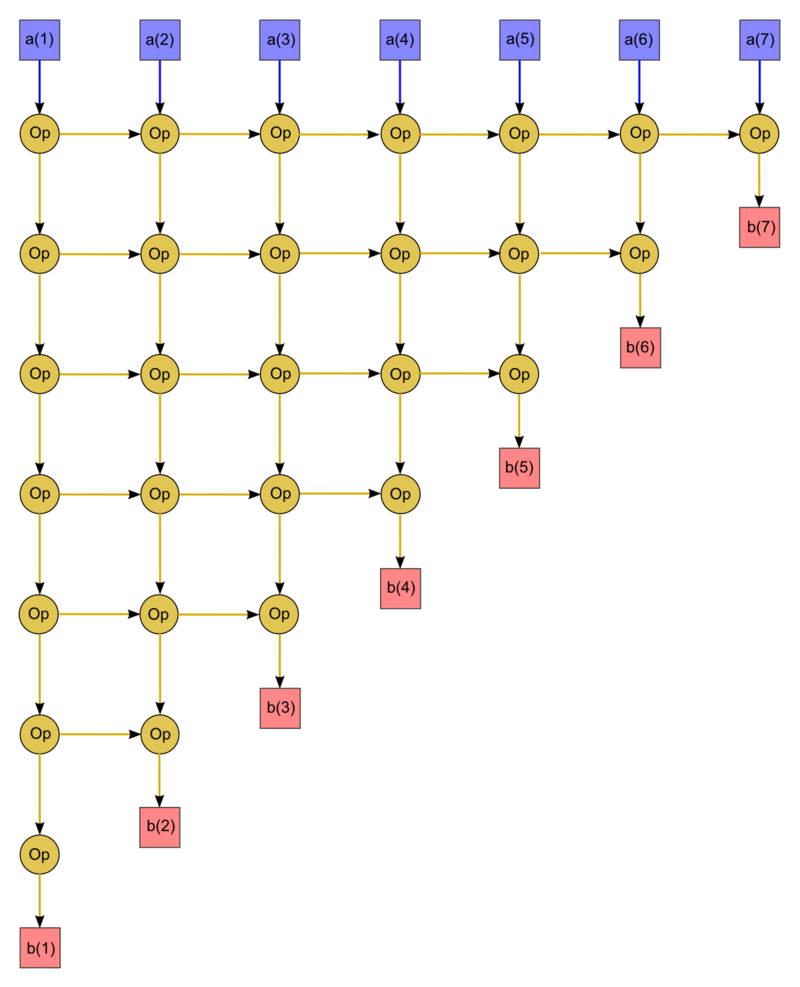
1.7 Информационный граф

Опишем граф алгоритма в виде рисунка. Изображён граф для $n = 9$. Как видно, граф регулярный, занимает собой треугольную область. Каждая вершина соответствует операции $c d + e$.

Сдвиг аргументов многочлена по схеме Горнера, последовательный вариант

1.8 Описание ресурса параллелизма алгоритма

Последовательный вариант вычисления сдвига аргументов многочлена по схеме Горнера, несмотря на название, имеет хороший ресурс параллелизма. В получившемся алгоритме высота параллельной формы будет равна $n$ операций умножения плюс $n$ операций сложения (и равна, таким образом, высоте одной схемы Горнера). В таком виде алгоритм должен быть отнесён к алгоритмам линейной сложности по высоте параллельной формы. Ширина параллельной формы равна $n$, что даёт нам линейную сложность по ширине параллельной формы.

1.9 Описание входных и выходных данных

Входные данные: массив $a$ (элементы $a_i$ с номерами от $0$ до $n$), скаляр $\alpha$.

Дополнительные ограничения: отсутствуют.

Объём входных данных: $n + 2$.

Выходные данные: массив $b$ (элементы $b_k$ с номерами от $0$ до $n$).

Объём выходных данных: $n + 1$.

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является линейной функцией $\frac{(n + 1)}{2}$. При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных — также $\frac{(n + 1)}{2}$. При этом алгоритм полностью детерминирован. Дуги информационного графа локальны и регулярны.

2 Программная реализация

2.1 Особенности реализации последовательного алгоритма

На Фортране алгоритм можно записать так:

	DO I = 0, N
		b(I) = a(I)
	END DO
	DO J = N, 1, -1
		DO I = 1, J
			b(I) = b(I)+b(I-1)*alpha
		END DO
	END DO

При больших $n$ может оказаться полезным использовать блочную версию алгоритма, чтобы эффективно использовать кэш. Аналогичное соображение следует применять и для параллельных версий.