Скалярное произведение векторов, вещественная версия, последовательно-параллельный вариант
| Скалярное произведение векторов, вещественная версия, последовательно-параллельный вариант | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]2n-1[/math] |
| Объём входных данных | [math]2n[/math] |
| Объём выходных данных | [math]1[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(\sqrt{n})[/math] |
| Ширина ярусно-параллельной формы | [math]O(\sqrt{n})[/math] |
Основные авторы описания: А.В.Фролов.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Скалярное произведение векторов используется в качестве одной из базовых операций в широком круге методов. При этом используется как в версии скалярного произведения собственно [math]n[/math]-мерных векторов (одномерных массивов размера [math]n[/math]), так и в версии скалярного произведения строк, столбцов и других линейных подмножеств массивов большей размерности. Последняя отличается от первой тем, что соответствующая подпрограмма получает, кроме стартовых адресов векторов, также и параметры смещения следующих элементов относительно предыдущих (в первой версии эти смещения равны 1). Разные формулы существуют для скалярных произведений в вещественной арифметике и для комплексных векторов. Здесь мы рассматриваем только вещественную арифметику и последовательно-параллельную реализацию.
1.2 Математическое описание алгоритма
Исходные данные: два одномерных массива n чисел.
Вычисляемые данные: сумма попарных произведений элементов массива.
Формулы метода: число [math]n[/math] разлагается в выражение типа [math]n = (p - 1) k + q[/math], где [math]p[/math] — количество процессоров, [math]k = \lceil \frac{n}{p} \rceil[/math], [math]q = n - k (p - 1)[/math]. После этого на [math]i[/math]-м процессоре ([math]i \lt p[/math]) последовательно вычисляется «частичное» скалярное произведение подмассивов, начиная с [math](i - 1) k + 1[/math]-го номера элемента, до [math]ik[/math]-го номера.
- [math]S_i = \sum_{j = 1}^k a_{k (i - 1) + j} b_{k (i - 1) + j}[/math]
На [math]p[/math]-м процессоре последовательно вычисляется «частичное» скалярное произведение подмассивов, начиная с [math](p - 1) k + 1[/math]-го номера элемента до [math](p - 1) k + q[/math]-го номера.
- [math]S_p = \sum_{j = 1}^q a_{k (p - 1) + j} b_{k (p - 1) + j}[/math]
По окончании этого процесса процессоры обмениваются данными и на одном из них (либо на всех одновременно, если результат нужен далее на всех процессорах) получившиеся суммы суммируются последовательно друг с другом.
- [math]\sum_{i = 1}^p S_i[/math]
При этом в последовательно-параллельном варианте при вычислений сумм из формул используется последовательный порядок суммирования (обычно от меньших индексов к большим).
1.3 Вычислительное ядро алгоритма
Вычислительное ядро скалярного произведения в последовательно-параллельном варианте можно представить как [math]p[/math] вычислений «частных» скалярных произведений c последующим последовательным суммированием получившихся [math]p[/math] чисел.
1.4 Макроструктура алгоритма
Как уже записано в описании ядра алгоритма, основную часть вычисления скалярного произведения составляют параллельное вычисление скалярных произведений меньшей размерности последовательным методом и последовательное вычисление суммы получившихся «частных» скалярных произведений подмассивов.
1.5 Схема реализации последовательного алгоритма
Формулы метода описаны выше. Последовательность исполнения суммирования может быть разная — как по возрастанию, так и по убыванию индексов. Обычно без особых причин порядок не меняют, используя естественный (возрастание индексов).
1.6 Последовательная сложность алгоритма
Для вычисления скалярного произведения массивов, состоящих из [math]n[/math] элементов, при любых разложениях количество операций умножения неизменно и равно [math]n[/math], а количество операций сложения равно [math]n - 1[/math]. Поэтому алгоритм должен быть отнесён к алгоритмам линейной сложности по количеству последовательных операций.
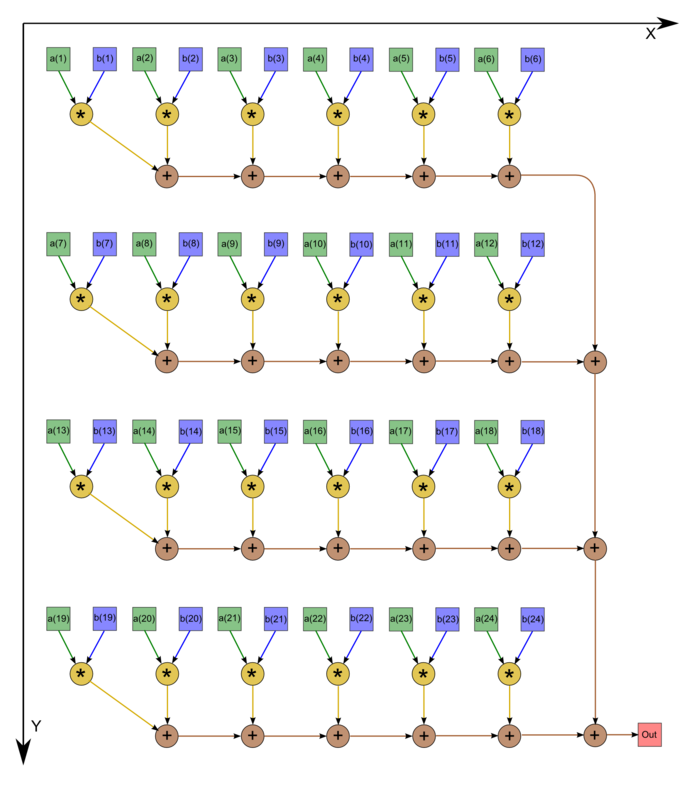
1.7 Информационный граф
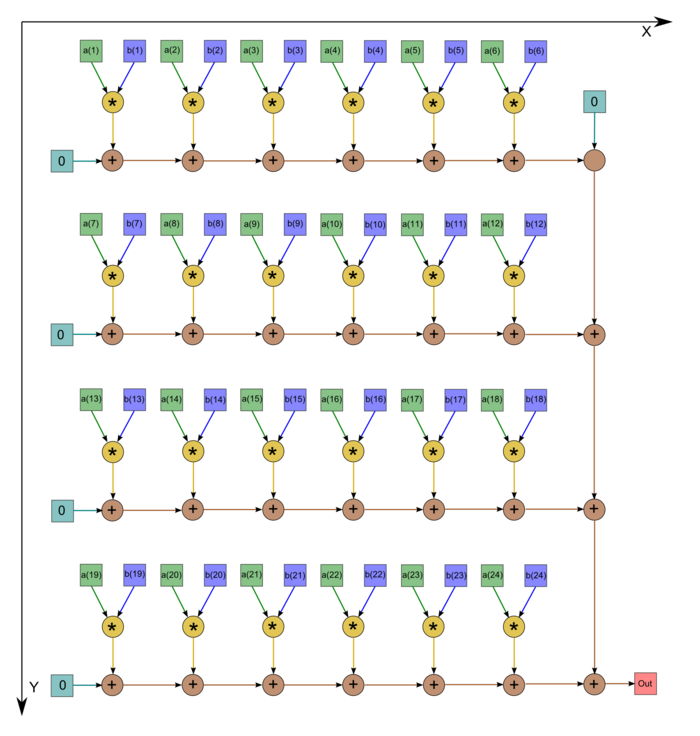
На рис.1 изображён граф аогоритма. Однако следует отметить, что в большинстве случаев программисты не экономят на одном вызове операции сложения, а инициализируют начальное значение переменной нулём. В этом случае граф становится таким, как на рис.2 (n=24).
1.8 Ресурс параллелизма алгоритма
Для вычисления скалярного произведения массивов порядка [math]n[/math] последовательно-параллельным методом в параллельном варианте требуется последовательно выполнить следующие ярусы:
- 1 ярус вычисления произведений,
- [math]k - 1[/math] ярусов суммирования по частям массивов ([math]p[/math] ветвей),
- [math]p - 1[/math] ярусов суммирования (одна последовательная ветвь).
Таким образом, в параллельном варианте критический путь алгоритма (и соответствующая ему высота ЯПФ) будет зависеть от произведённого разбиения массива на части. В оптимальном случае ([math]p = \sqrt{n}[/math]) высота ЯПФ будет равна [math] 2 \sqrt{n} - 1[/math]. При классификации по высоте ЯПФ, таким образом, последовательно-параллельный метод относится к алгоритмам со сложностью «корень квадратный». При классификации по ширине ЯПФ его сложность также будет «корень квадратный».
1.9 Входные и выходные данные алгоритма
Входные данные: массивы [math]a[/math] (элементы [math]a_i[/math]), [math]b[/math] (элементы [math]b_i[/math]).
Дополнительные ограничения: отсутствуют.
Объём входных данных: [math]2 n[/math].
Выходные данные: сумма попарных произведений элементов массивов.
Объём выходных данных: один скаляр.
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является корнем квадратным (отношение линейной к корню квадратному). При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных — всего-навсего 1 (входных и выходных данных почти столько же, сколько операций; если точнее - даже больше на 2). При этом алгоритм полностью детерминирован при заданном разложении [math]n[/math]. Дуги информационного графа локальны. Для уменьшения ошибок округления режимом накопления в ряде алгоритмов, использующих скалярное произведение одинарной точности, оно вычисляется с двойной точностью. Впрочем, у последовательно-параллельного способа вычисления скалярного произведения и без режима накопления влияние ошибок округления «в среднем» меньше в [math]\sqrt{n}[/math] раз.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
В простейшем (без перестановок суммирования) варианте на Фортране можно записать так:
DO I = 1, P
S (I) = A(K*(I-1)+1)*B(K*(I-1)+1)
IF (I.LQ.P) THEN
DO J = 2,K
S(I)=S(I)+A(K*(I-1)+J)*B(K*(I-1)+J)
END DO
ELSE
DO J = 2,Q
S(I)=S(I)+A(K*(I-1)+J)*B(K*(I-1)+J)
END DO
END IF
END DO
SCP = S(1)
DO I = 2, P
SCP = SCP + S(I)
END DO
Можно записать и аналогичные схемы, где суммирование будет проводиться в обратном порядке. Подчеркнём, что граф алгоритма обеих схем — один и тот же! Тело первого цикла целиком может быть заменено вызовом функции скалярного произведения, если она реализована в последовательном варианте.
2.2 Возможные способы и особенности параллельной реализации алгоритма
Помимо выписанной выше простейшей реализации, существуют более сложные коды, реализующие тот же алгоритм. Следует обратить внимание на то, что ряд реализаций (в том же BLAS) использует разложение [math]n[/math] на небольшое и большое числа. При этом внутренние циклы не используются, поскольку суммирование небольшого числа произведений проводится «вручную›, увеличением тела первого цикла. Часть реализаций последовательно-параллельного метода вычисления скалярного произведения не оформлена в виде отдельных подпрограмм, а раскидана по тексту программы алгоритма, использующего скалярное произведение, но фактически представляет именно такую реализацию. Примером этого могут быть блочные реализации различных разложений (Холецкого, Гаусса и др.).