Скалярное произведение векторов, вещественная версия, последовательный вариант

1 Описание свойств и структуры алгоритма

1.1 Словесное описание алгоритма

Скалярное произведение векторов используется в качестве одной из базовых операций в широком круге методов. При этом используется как в версии скалярного произведения собственно [math]n[/math]-мерных векторов (одномерных массивов размера [math]n[/math]), так и в версии скалярного произведения строк, столбцов и других линейных подмножеств массивов большей размерности. Последняя отличается от первой тем, что соответствующая подпрограмма получает, кроме стартовых адресов векторов, также и параметры смещения следующих элементов относительно предыдущих (в первой версии эти смещения равны 1). Разные формулы существуют для скалярных произведений в вещественной арифметике и для комплексных векторов. Здесь мы рассматриваем только вещественную арифметику.

1.2 Математическое описание

Исходные данные: два одномерных массива [math]n[/math] чисел.

Вычисляемые данные: сумма попарных произведений элементов массива.

Формулы метода: для векторов [math]\vec{a}[/math] и [math]\vec{b}[/math] размерности [math]n[/math] вычисляется сумма [math]\sum_{i = 1}^n a_i b_i[/math].

При этом в последовательном варианте используется последовательный порядок суммирования (обычно от меньших индексов к большим). Существуют и другие способы вычисления скалярного произведения, но здесь мы их рассматривать не будем.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро скалярного произведения в последовательном варианте можно представить либо (с предварительной инициализацией «накопителя» нулём) в качестве набора [math]n[/math] «двойных» операций (попарное умножение соответствующих элементов массивов и добавление результата к уже накопленной части скалярного произведения), либо в качестве одного попарного умножения первых элеменов массива и набора [math]n-1[/math] «двойных» операций (попарное умножение соответствующих элементов массивов и добавление результата к уже накопленной части скалярного произведения). Последняя версия более экономна по операциям с вещественной арифметикой, однако широко используется и первая, с одним «холостым» вычислением суммы числа и нуля. Это связано с более простой записью кода у первой версии. Интересно, что, несмотря на разные графы, эти версии дают одинаковые результаты с точностью до бита, поэтому выбор одной из них никак не влияет на ошибки округления.

1.4 Макроструктура алгоритма

Как уже записано в описании ядра алгоритма, основную часть вычисления скалярного произведения составляет массовый последовательный набор «двойных» операций (попарное умножение соответствующих элементов массивов и добавление результата к уже накопленной части скалярного произведения).

1.5 Описание схемы реализации последовательного алгоритма

Формулы метода описаны выше. Последовательность исполнения суммирования может быть разная - как по возрастанию, так и по убыванию индексов. Обычно без особых причин порядок не меняют, используя естественный (возрастание индексов).

1.6 Последовательная сложность алгоритма

Для вычисления скалярного произведения массивов, состоящих из [math]N[/math] элементов, при любых разложениях количество операций умножения неизменно и равно [math]N[/math], а количество операций сложения в зависимости от варианта (см. п. 3) равно [math]N-1[/math] или [math]N[/math]. Поэтому алгоритм должен быть отнесён к алгоритмам линейной сложности по количеству последовательных операций.

1.7 Информационный граф

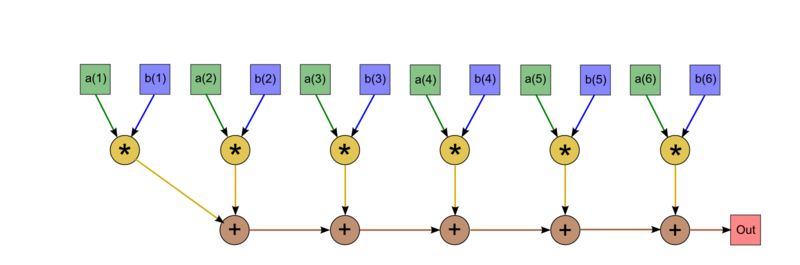
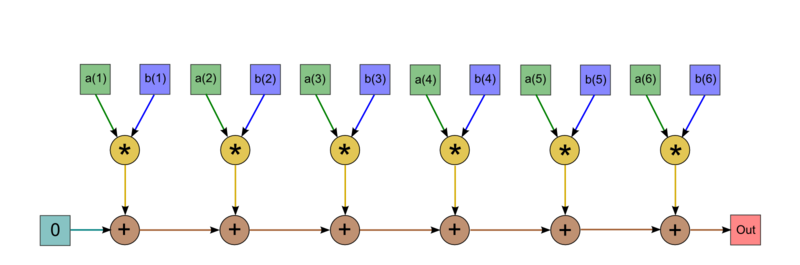
Опишем граф алгоритма в виде рисунков. На верхнем рисунке граф варианта без «холостого» суммирования. Однако следует отметить, что в большинстве случаев программисты не экономят на одном вызове операции сложения, а инициализируют начальное значение переменной нулём. В этом случае граф становится таким, как на втором рисунке. Приведён граф вычисления скалярного произведения последовательным способом при [math]n = 6[/math].

Скалярное произведение с экономией операций сложения

Скалярное произведение без экономии операций сложения

1.8 Описание ресурса параллелизма алгоритма

Последовательный вариант вычисления скалярного произведения , несмотря на название, имеет ресурс параллелизма степени 2. Дело в том, что, если рассматривать отдельно умножения и сложения, то видно, что при выполнении очередного сложения «подготовительное» умножение к следующему можно выполнить заранее. В принципе, можно, если использовать дополнительную память для хранения всех попарных произведений, вообще выполнить их всех параллельно, а потом последовательно выполнить суммирование вычисленных произведений. Таким образом, в получившемся алгоритме высота параллельной формы будет равна 1 операции умножения плюс [math]N - 1[/math] операций сложения. В таком виде алгоритм должен быть отнесён к алгоритмам линейной сложности как по высоте, так и по ширине параллельной формы. Однако если мы будем последовательно выполнять и умножения, то ширина параллельной формы может быть уменьшена до 2, что даёт нам постоянную сложность по ширине параллельной формы.

1.9 Описание входных и выходных данных

Входные данные: массивы [math]a[/math] (элементы [math]a_i[/math]), [math]b[/math] (элементы [math]b_i[/math]).

Дополнительные ограничения: отсутствуют.

Объём входных данных: [math]2 n[/math].

Выходные данные: сумма попарных произведений элементов массивов.

Объём выходных данных: один скаляр.

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является константой (2). При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных — всего-навсего 1 (входных и выходных данных почти столько же, сколько операций; если точнее — даже больше на 2). При этом алгоритм полностью детерминирован. Дуги информационного графа локальны. Для уменьшения ошибок округления режимом накопления в ряде алгоритмов, использующих скалярное произведение одинарной точности, оно вычисляется с двойной точностью.

2 Программная реализация

2.1 Особенности реализации последовательного алгоритма

В простейшем (входные данные — вектора) варианте на Фортране можно записать так:

	SCP = A(1)*B(1)
	DO I = 2, N
		SCP = SCP + A(I)*B(I)
	END DO

В варианте с «холостым» сложением запись такая:

	SCP = 0.
	DO I = 1, N
		SCP = SCP + A(I)*B(I)
	END DO

2.2 Описание локальности данных и вычислений

2.2.2 Описание локальности реализации алгоритма

2.2.2.1 Описание структуры обращений в память и качественная оценка локальности

Рисунок 12.1. Реализация скалярного произведения. Профиль обращений в память

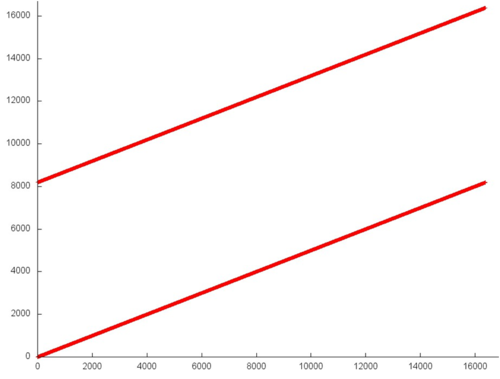
На рисунке 12.1 представлен профиль обращений в память для последовательной реализации скалярного произведения. В алгоритме задействованы два массива, и мы можем увидеть две прямые, которые соответствуют последовательным переборам элементов данных массивов. Все обращения в память в данной реализации обеспечиваются одной операцией

sum += a[i]*b[i];

В данном случае мы без более детального рассмотрения графика профиля обращений в память можем понять, что профиль обращений устроен следующим образом:

0,i,1,i+1,2,i+2,…

т.е. прямые на графике состоят исключительно из последовательных обращений в двум массивам.

Подобный профиль позволяет говорить об очень низкой временно́й локальности, поскольку повторные обращения к данным отсутствуют совсем. Однако пространственная локальность достаточно высока из-за последовательного перебора. Стоит отметить, что расстояние по памяти между соседними обращениями n и n+1 велико (равно размеру массива), однако расстояние по памяти между обращениями n и n+2 всегда равно 1, что и обеспечивает высокую пространственную локальность.

2.2.2.2 Количественная оценка локальности

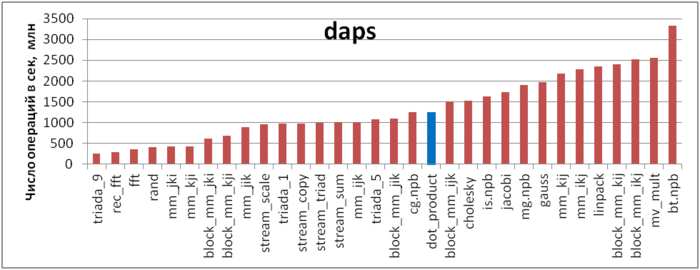
Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.

На рисунке 12.2 значения приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что в целом данная реализация показывает средние результаты по производительности работы с памятью. Интересно, что значение daps оказалось несколько выше, чем у всех реализаций triada. По всей видимости, это может быть связано с тем, что в триаде присутствует операция записи элементов массива в память, в то время как в реализации скалярного произведения требуется только чтение данных массива из памяти.

Рисунок 12.2. Сравнение значений оценки daps

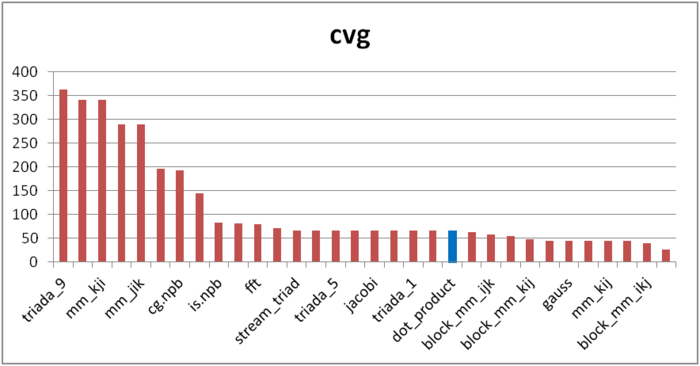
Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность.

Рисунок 12.3. Сравнение значений оценки cvg

На рисунке 12.3 значения приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Можно увидеть, что, согласно данной оценке, реализация скалярного произведения оказалась выше в списке по сравнению с оценкой daps. Это связано, в первую очередь, с высокой пространственной локальностью.

2.7 Существующие реализации алгоритма

Помимо выписанных выше простейших реализаций, существуют более сложные коды, реализующие тот же алгоритм. Это объясняется тем, что порой чисто программистскими приёмами оптимизируют работу с регистрами, с кэшем и т. п. В частности, даже в Линпаке есть разные реализации кода — из BLAS или другие варианты. Большинство их сводится к сведению одинарного цикла длиной n к двойному циклу либо к одинарному с меньшим числом итераций, но более длинной операцией в теле цикла. Между тем, разбиения циклов на группы для вычислений частных сумм в скалярном произведении могут быть полезны и для лучшего использования кэша на отдельных узлах, когда самих скалярных произведений вычисляется сразу много и распараллеливание программы состоит в их распределении между узлами.