Умножение плотной неособенной матрицы на вектор (последовательный вещественный вариант)

Основные авторы описания: А.В.Фролов, Вад.В.Воеводин (раздел 2.2), А.М.Теплов (раздел 2.4)

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Умножение матрицы на вектор - одна из базовых задач в алгоритмах линейной алгебры, широко применяется в большом количестве разных методов. Здесь мы рассмотрим умножение [math]y = Ax[/math] плотной неособенной матрицы на вектор (последовательный вещественный вариант), то есть тот вариант, где никак не используются ни специальный вид матрицы, ни ассоциативные свойства операции сложения.

1.2 Математическое описание алгоритма

Исходные данные: плотная матрица [math]A[/math] (элементы [math]a_{ij}[/math]), умножаемый на неё вектор [math]x[/math] (элементы [math]x_{i}[/math]).

Вычисляемые данные: вектор решения [math]y[/math] (элементы [math]y_{i}[/math]).

Формулы метода:

[math] \begin{align} y_{i} = \sum_{j = 1}^{n} a_{ij} x_{j}, \quad i \in [1, m]. \end{align} [/math]

Существует также блочная версия метода, однако в данном описании разобран только точечный метод.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро умножения матрицы на вектор можно составить из множественных (всего их [math]m[/math]) вычислений скалярных произведений строк матрицы [math]A[/math] вектор [math]x[/math]:

[math] \sum_{j = 1}^{n} a_{ij} x_{j}[/math]

в режиме накопления или без него, в зависимости от требований задачи.

1.4 Макроструктура алгоритма

Как уже записано в описании ядра алгоритма, основную часть умножения матрицы на вектор составляют множественные (всего [math]m[/math]) вычисления скалярных произведений строк матрицы [math]A[/math] вектор [math]x[/math]

[math] \sum_{j = 1}^{n} a_{ij} x_{j}[/math]

в режиме накопления или без него.

1.5 Схема реализации последовательного алгоритма

Для всех [math]i[/math] от [math]1[/math] до [math]m[/math] по возрастанию выполняются

[math]y_{i} = \sum_{j = 1}^{n} a_{ij} x_{j}[/math]

Особо отметим, что вычисления сумм вида [math]\sum_{j = 1}^{n} a_{ij} x_{j}[/math] производят в режиме накопления прибавлением к текущему (временному) значению вычисляемой компоненты вектора [math]y_{i}[/math] произведений [math]a_{ij} x_{j}[/math] для [math]j[/math] от [math]1[/math] до [math]n[/math], c возрастанием [math]j[/math], вначале все компоненты инициализируются нулями. При суммировании "по убыванию" общая схема принципиально не отличается и потому нами не рассматривается. Другие порядки выполнения суммирования приводят к изменению параллельных свойств алгоритма и будут рассматриваться нами в отдельных описаниях.

1.6 Последовательная сложность алгоритма

Для умножения квадратной матрицы на вектор порядка [math]n[/math] (т.е. при [math]m=n[/math]) в последовательном (наиболее быстром) варианте требуется:

• по [math]n^2[/math] умножений и сложений.

Для умножения матрицы размером [math]m[/math] строк на [math]n[/math] столбцов на вектор порядка [math]n[/math] в последовательном (наиболее быстром) варианте требуется:

• по [math]mn[/math] умножений и сложений.

При этом использование режима накопления требует совершения умножений и сложений в режиме двойной точности (или использования функции вроде DPROD в Фортране), что ещё больше увеличивает затраты во времени, требуемом для выполнения умножения матрицы на вектор.

При классификации по последовательной сложности, таким образом, алгоритм умножения матрицы на вектор относится к алгоритмам с квадратической сложностью (в случае неквадратной матрицы - с билинейной).

1.7 Информационный граф

Опишем граф алгоритма как аналитически, так и в виде рисунка.

Рисунок 1. Граф последовательного умножения плотной матрицы на вектор с отображением входных и выходных данных

Граф алгоритма умножения плотной матрицы на вектор состоит из одной группы вершин, расположенной в целочисленных узлах двумерной области, соответствующая ей операция [math]a+bc[/math].

Естественно введённые координаты области таковы:

• [math]i[/math] — меняется в диапазоне от [math]1[/math] до [math]m[/math], принимая все целочисленные значения;
• [math]j[/math] — меняется в диапазоне от [math]1[/math] до [math]n[/math], принимая все целочисленные значения.

Аргументы операции следующие:

• [math]a[/math]:
  • при [math]j = 1[/math] константа [math]0.[/math];
  • при [math]j \gt 1[/math] — результат срабатывания операции, соответствующей вершине с координатами [math]i, j-1[/math];
• [math]b[/math] — элемент входных данных, а именно [math]a_{ij}[/math];
• [math]c[/math] - элемент входных данных [math]x_{j}[/math];

Результат срабатывания операции является:

• при [math]j \lt n[/math] - промежуточным данным алгоритма;
• при [math]j = n[/math] - выходным данным.

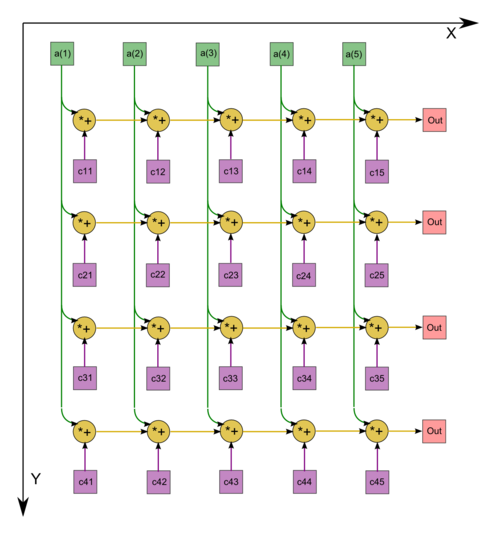
Описанный граф можно посмотреть на рисунке, выполненном для случая [math]m = 4, n = 5[/math]. Здесь вершины обозначены голубым цветом. Изображена подача только входных данных из вектора [math]x[/math], подача элементов матрицы [math]A[/math], идущая во все вершины, на рисунке не представлена.

1.8 Ресурс параллелизма алгоритма

Для алгоритма умножения квадратной матрицы на вектор порядка n в параллельном варианте требуется последовательно выполнить следующие ярусы:

• по [math]n[/math] ярусов умножений и сложений (в каждом из ярусов — [math]n[/math] операций).

Для умножения матрицы размером [math]m[/math] строк на [math]n[/math] столбцов на вектор порядка [math]n[/math] в последовательном (наиболее быстром) варианте требуется:

• по [math]n[/math] ярусов умножений и сложений (в каждом из ярусов — [math]m[/math] операций).

При этом использование режима накопления требует совершения умножений и сложений в режиме двойной точности, а в параллельном варианте это означает, что практически все промежуточные вычисления для выполнения алгоритма в режиме накопления должны быть двойной точности. В отличие от последовательного варианта это означает некоторое увеличение требуемой памяти.

При классификации по высоте ЯПФ, таким образом, алгоритм умножения матрицы на вектор относится к алгоритмам с линейной сложностью. При классификации по ширине ЯПФ его сложность также будет линейной.

1.9 Входные и выходные данные алгоритма

Входные данные: матрица [math]A[/math] (элементы [math]a_{ij}[/math]), вектор [math]x[/math] (элементы [math]x_{i}[/math]).

Объём входных данных: [math]mn+n[/math] .

Выходные данные: вектор [math]y[/math] (элементы [math]y_{i}[/math]).

Объём выходных данных: [math]m[/math].

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является линейным (отношение квадратической или билинейной к линейной).

При этом вычислительная мощность алгоритма умножения матрицы на вектор, как отношение числа операций к суммарному объему входных и выходных данных – всего лишь константа.

При этом алгоритм умножения матрицы на вектор полностью детерминирован. Использование другого порядка выполнения ассоциативных операций в данной версии нами не рассматривается.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

В простейшем варианте алгоритм умножения матрицы на вектор на Фортране можно записать так:

         
	DO  I = 1, M
		S = 0.
		DO  J = 1, N
			S = S + DPROD(A(I,J), X(J))
		END DO	
	        Y(I) = S
	END DO

При этом для реализации режима накопления переменная [math]S[/math] должна быть двойной точности.

2.2 Локальность данных и вычислений

2.2.1 Локальность реализации алгоритма

2.2.1.1 Структура обращений в память и качественная оценка локальности

Рисунок 2. Умножение плотной матрицы на вектор. Общий профиль обращений в память

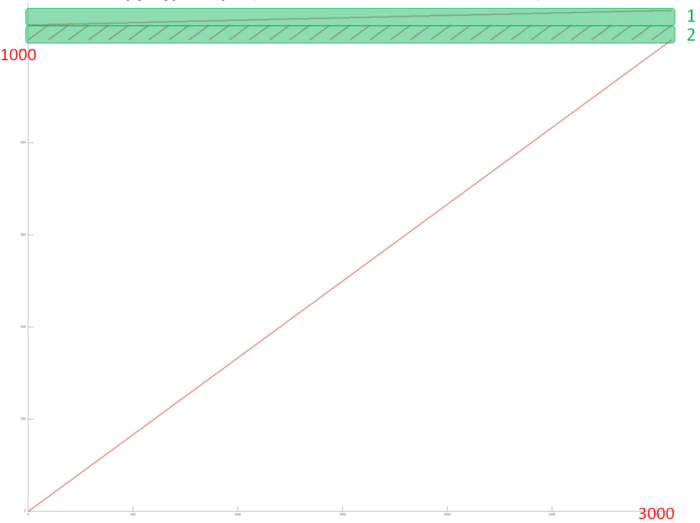
На рис.2 представлен профиль обращений в память для реализации умножения плотной матрицы на вектор. В данном алгоритме задействовано три массива. Выделенный зеленым фрагмент 1 образован обращениями к результирующему вектору; фрагмент 2 – обращениями к исходному вектору; остальные обращения (фрагмент 3) выполняются к матрице, на которую умножается исходный вектор.

Если посмотреть на исходный код, становится понятным, что каждый фрагмент устроен очень просто:

for(int i = 0; i < size; i++)
for(int j = 0; j < size; j++)
vec_out[i] += matrix[i][j] * vec_in[j];

Видно, что фрагмент 1 (обращения к массиву vec_out) состоит из последовательного перебора всех элементов вектора, только к каждому элементу происходит подряд size обращений. Во фрагменте 2 (массив vec_in) выполняется обычный последовательный перебор, который затем повторяется size раз. Фрагмент 3 также представляет собой последовательный перебор всех элементов матрицы, который выполняется только один раз.

Самой высокой локальностью обладает фрагмент 1 из-за повторяющихся подряд обращений к одним и тем же элементам. Однако фрагмент 2 также обладает высокой как пространственной, так и временной локальностью, поскольку число повторных проходов достаточно велико. Фрагмент 3, как и остальные, характеризуется высокой пространственной локальностью (из-за последовательного перебора), однако очень низкой временной локальностью – повторные обращения в нем просто отсутствуют.

2.2.1.2 Количественная оценка локальности

Основной фрагмент реализации, на основе которого были получены количественные оценки, приведен здесь (функция Kernel). Условия запуска описаны здесь.

Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.

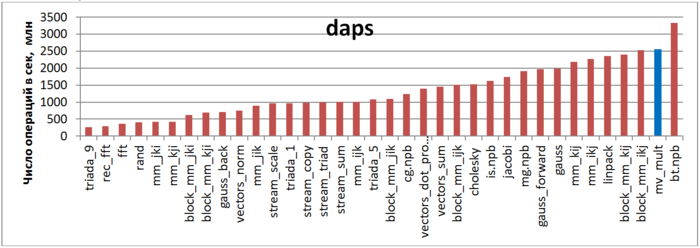
На рис.3 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что производительность данной программы очень высока, даже немного выше, чем производительность теста Linpack. Одна из основных причин этому – очень высокая локальность обращений к векторам.

Рисунок 3. Сравнение значений оценки daps

Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность.

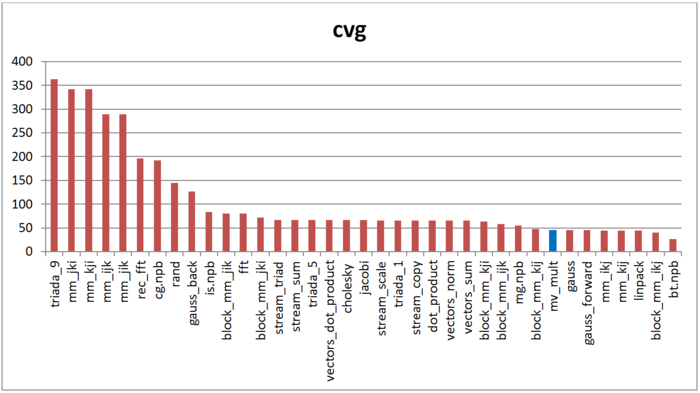
На рис.4 приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Можно увидеть, что, согласно данной оценке, локальность реализации умножения матрицы на вектор высока, хотя и не среди первых значений. Однако можно заметить, что полученное значение лишь совсем немного ниже оценки cvg для, например, реализации метода Гаусса или лучших вариантов перемножения матрицы.

Рисунок 4. Сравнение значений оценки cvg

2.4 Масштабируемость алгоритма и его реализации

2.4.2 Масштабируемость реализации алгоритма

Рисунок 5. Параллельная реализация произведения матрицы на вектор Максимальная производительность.

Рисунок 6. Параллельная реализация произведения матрицы на вектор Максимальная эффективность.

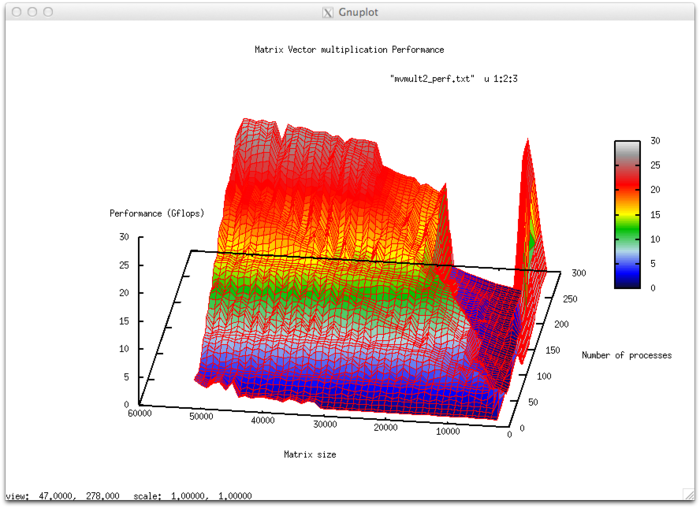
Набор изменяемых параметров запуска реализации алгоритма и границы значений параметров алгоритма:

• число процессоров [4 : 256]
• размерность матрицы [1024 : 51200]

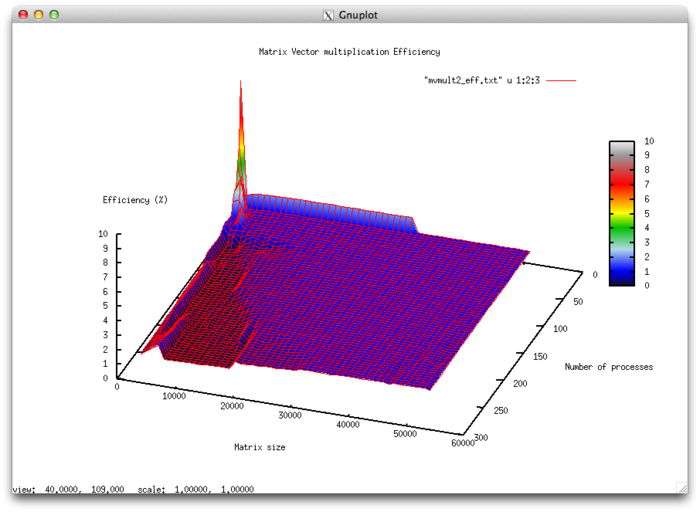
Эффективность выполнения реализации алгоритма

• Минимальная эффективность 0,02%
• Максимальная эффективность 9,55%

Оценка масштабируемости

• По числу процессов: -0.01517 – при увеличении числа процессов эффективность убывает достаточно интенсивно на всей рассмотренной области изменений параметров запуска. Уменьшение эффективности на рассмотренной области работы параллельной программы звязано с увеличением числа пересылок с ростом числа процессов и как следствие ростом накладных расходов на организацию вычислений. Основной вклад в значение эффективности вносит область с малым числом процессов и малой задачей, там эффективность достигает максимума в 9,5%. Далее эффективность очень резко падает до уровня около 1% Присутствует область, на которой при увеличении числа процессов эффективность возрастает, но при дальнейшем росте продолжает снижаться. Это скорее всего объясняется декомпозицей данных, при которой наступает момент, когда размер матрицы позволяет блокам укладываться в КЭШ-память. Так же это подтверждает проявление этого явления, но со смещением по числу процессов, и при увеличении вычислительной сложности задачи.
• По размеру задачи: -0.0014 – при увеличении размера задачи эффективность в целом уменьшается по рассматриваемой области, хотя и менее интенсивно, чем при увеличении числа процессов. Снижение эффективности объясняется тем, что при росте вычислительной сложности существенно возрастают объемы передаваемых данных. При увеличении размера данных наступает момент резкого снижения эффективности с значений около 1% к долям процента и минимуму. С увеличением числа процессоров такой переход появляется на большем объеме данных. Это свидетельствует о том, что присутствует момент, когда данных слишком много и эффективность работы с ними становится значительно ниже, но чем больше имеется процессов, там позже наступает такой момент декомпозиции. Присутствует область возрастания эффективности, на всех рассмотренных размерах матрицы. Это объясняется тем, что при малом размере задачи данные хорошо укладываются в КЭШ память, что приводит к высокой эффективности работы приложения при малом размере задачи. При дальнейшем увеличении размера эффективность уменьшается при выходе за границы КЭШ-памяти.
• По двум направлениям: -0.0001546 – при рассмотрении увеличения, как вычислительной сложности, так и числа процессов по всей рассмотренной области значений уменьшается, интенсивность уменьшения эффективности не очень высока. В совокупности с тем фактом, что разница между максимальной и минимальной эффективностью на рассмотренной области значений параметров составляет около 9% говорит о том, что уменьшение эффективности по всей области довольно равномерное, но интенсивно лишь в не очень больших участках по площади. На остальной области значений параметров изменения эффективности не столь значительны и находятся на приблизительно одном и том же уровне.

Реализация алгоритма на языке C