Участник:Антон Тодуа/Partitioning Around Medoids (PAM)
 | Эта работа успешно выполнена Преподавателю: в основное пространство, в подстраницу Данное задание было проверено и зачтено. Проверено Dexter и Zhum. |
| Partitioning Around Medoids | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(Q * K * N^2)[/math] |
| Объём входных данных | [math]\frac{N (N - 1)}{2}[/math] |
| Объём выходных данных | [math]K[/math] медоидов или [math]N[/math] кластеров объектов |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(Q * K * N)[/math] |
| Ширина ярусно-параллельной формы | [math]O(K * (N - K))[/math] |
Авторы:
- Тодуа А.Р. (оценки и реализация)
- Гусева Ю.В. (описание алгоритма)
Вклад авторов следует считать равноценным.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Алгоритм PAM (Partitioning Around Medoids) был предложен Чарли Кауфаманом (Charlie Kaufman) и Питером Русивом (Peter Rousseeuw) в 1987[1]. Алгоритм является одним из распространённых вариантов реализации [math]k[/math]-medoids.
PAM используется для выполнения кластеризации[1] объектов — процесса автоматического разбиения некоторого множества объектов на кластеры (множества) на основе их схожести (наиболее схожие объекты, как правило, располагаются в одном кластере). В качестве исходных данных алгоритму необходима симметрическая матрица с нолями на главной диагонали (dissimilarity matrix), задающая расстояние (в смысле похожести) между объектами, для которых выполняется кластеризация и число кластеров, по которым следует распределить объекты. Стоит отметить, что не все алгоритмы кластеризации требует задания количества кластеров, например, методы иерархической[2] кластеризации свободны от данного ограничения.
Алгоритм PAM для каждого кластера в качестве его характерного представителя выбирает наиболее подходящий из объектов кластеризации. Выбранные объекты называются медоидами (medoids). Алгоритм состоит из двух стадий. Первая стадия – BUILD предназначена для выбора исходного множества медоидов. Вторая стадия – SWAP является итерационной. На каждой итерации стадии SWAP алгоритм пытается улучшить выбранное множество медоидов с помощью выполнения операции обмена, которая представляет собой замену одного медоида на один из объектов кластеризации. Алгоритм завершает свою работу, когда ни один из возможных обменов не позволяет улучшить разбиение на кластеры. Часто на практике, условием завершения работы алгоритма также является момент, когда наилучшее возможное улучшение кластеризации меньше заранее выбранной пороговой величины. Введение данной величины позволяет сократить число итераций. Последнее, однако, снижает качество кластеризации (иногда незначительно).
1.2 Математическое описание алгоритма
В качестве исходных данных алгоритм принимает:
- Симметрическую матрицу [math]D[/math] порядка [math]N[/math] с нолями на главной диагонали для [math]N[/math] объектов кластеризации: [math]i[/math]-я строка матрицы [math]D[/math] определяет расстояние от [math]i[/math]-го объекта до каждого из остальных объектов
- Требуемое число кластеров [math]K[/math], при этом: [math]K \lt N[/math]
Для заданных входных данных, алгоритм выбирает [math]K[/math] объектов - медоидов (medoids) из [math]N[/math] объектов кластеризации. Все медоиды относится к разных кластерам и являются их характерными представителями. Кластеры остальных объектов (не медоидов) совпадают с кластером ближайшего к ним медоида. Ближайший к [math]i[/math]-му объекту медоид будем коротко назвать медоидом [math]i[/math]-го объекта. Выбор медоидов осуществляется исходя из минимизации среднего расстояния (average dissimilarity) между объектами внутри одного кластера. От минимизации среднего расстояния можно перейти к минимизации суммы расстояний от объектов до их медоидов. Такой переход не повлияет на выбор медоидов, но позволит не накапливать ошибки округления, возникающие в результате операции деления. Стоит отметить, что в общем случае расстояние между объектами следует понимать как меру похожести (similarity) объектов.
Для дальнейшего описания алгоритма введём следующие обозначения:
- [math]U[/math] – множество объектов кластеризации, не выбранных в качестве медоидов
- [math]S[/math] – множество объектов кластеризации, выбранных в качестве медоидов
- [math]C_{ij}[/math] – изменение расстояния от [math]j[/math]-го объекта до его медоида в результате выбора [math]i[/math]-го объекта в качестве медоида
- [math]T_{ijh}[/math] – изменение расстояния от [math]j[/math]-го объекта до его медоида, в результате обмена [math]i[/math]-го медоида на [math]h[/math]-й объект
Под обменом [math]i[/math]-го медоида на [math]h[/math]-й объект будем понимать операцию, в результате которой [math]i[/math]-й медоид перестаёт быть медоидом, а [math]h[/math]-й объект выбирается в качестве медоида:
- [math] \begin{align} S & = S - \{i\} + \{h\} \\ U & = U - \{h\} + \{i\} \end{align} [/math]
Перед выполнением алгоритма множество [math]U[/math]содержит все объекты кластеризации, а множество [math]S[/math] – пусто. Описание значений [math]C_{ij}[/math] и [math]T_{ijh}[/math] и способа их вычисления будет дано при описании макроструктуры алгоритма.
Выполнение алгоритма включает в себя подготовительную стадию BUILD и итерационную стадию SWAP.
Стадия BUILD предназначена для построения начального множества медоидов и состоит в последовательном выполнении следующих шагов:
1. Добавить в множество [math]S[/math] объект, сумма расстояний от которого до всех остальных объектов минимальна (самый центральный объект):
[math]S = S + \{ arg\min_{i \in U} \sum_{j \in U} d_{ij} \}[/math]
2. Выбрать ещё [math]K-1[/math] медоидов следующим образом
[math]S = S + \{ arg\max_{i \in U} \sum_{j \in U - \{i\}} C_{ij} \}[/math]
Стадия SWAP является итерационной, одна итерация состоит в попытке улучшить кластеризацию путём выполнения обмена. На каждой итерации выполняется операция [math]arg\min_{i \in S, h \in U} \sum_{j \in U + \{i\}} T_{ijh}[/math]. Если для найденной пары [math]i \in S[/math] и [math]h \in U[/math] значение [math]\sum_{j \in U + \{i\}} T_{ijh}[/math] меньше ноля (это означает, что кластеризацию можно улучшить), то выполняется обмен [math]i[/math]-го медоида и [math]h[/math]-го объекта. В противном случае дальнейшее улучшение кластеризации с помощью обмена невозможно и алгоритм завершает свою работу.
В результате работы алгоритма множество [math]S[/math] будет содержать ровно [math]K[/math] объектов – медоидов. Как было сказано [math]j[/math]-й объект лежит в том же кластере, что и его медоид: [math]arg\min_{i \in S} d_{ij}[/math]
1.3 Вычислительное ядро алгоритма
Из математического описания алгоритма следует, что вычислительное ядро алгоритма сосредоточено в итерационной стадии SWAP. Одна итерация состоит в вычислении:
[math]arg\min_{i \in S, h \in U} \sum_{j \in U + \{i\}} T_{ijh}[/math]
Смысл этого выражения в том, что выполняется выбор такой пары медоида [math]i[/math] и объекта [math]h[/math] операция обмена которых приведёт к улучшению кластеризации или же делается вывод о невозможности такого обмена и работа алгоритма завершается.
1.4 Макроструктура алгоритма
Для описания значений [math]C_{ij}[/math] и [math]T_{ijh}[/math] и способа их вычисления введём следующие обозначения (в дополнение к обозначениям, введённым в математическом описании алгоритма):
- [math]D_{i}[/math] – расстояние от [math]i[/math]-го объекта до его медоида
- [math]E_{i}[/math] – расстояние от [math]i[/math]-го объекта до второго ближайшего к нему медоида
Очевидно, что для любых объектов верно неравенство [math]D_{i} \lt = E_{i}[/math]. Отметим также, что значения [math]D_{i}[/math] и [math]E_{i}[/math] могут меняться при изменениях в множествах [math]U[/math] и [math]S[/math], следовательно они должны пересчитываться после добавления нового медоида или выполнения операции обмена.
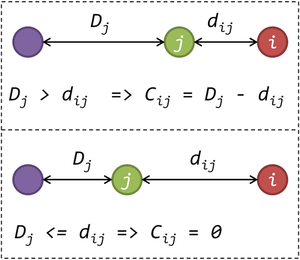
Значение [math]C_{ij}[/math] представляет собой число, на которое уменьшается значение [math]D_{j}[/math] в результате выбора [math]i[/math]-го объекта в качестве медоида. Очевидно, что данное значение всегда неотрицательно. Для вычисления [math]C_{ij}[/math] следует рассмотреть два случая. В первом случае, когда [math]D_{j} \lt = d_{ij}[/math], величина [math]D_{j}[/math] не изменится, т.к. ближайший к [math]j[/math]-му объекту медоид останется на том же расстоянии от него, следовательно будет справедливо равенство [math]C_{ij} = 0[/math]. Во втором случае, когда [math]D_{j} \gt d_{ij}[/math], ближайшим к [math]j[/math]-му объекту медоидом станет новый выбранный медоид ([math]i[/math]-ый объект), следовательно будет справедливо равенство [math]C_{ij} = D_{j} - d_{ij}[/math].
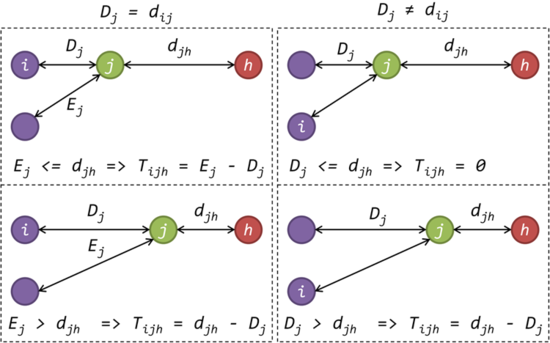
Значение [math]T_{ijh}[/math] представляет собой число, которое добавляется к значению [math]D_{j}[/math] в результате выполнения операции обмена [math]i[/math]-го медоида и [math]h[/math]-го объекта. Для вычисления [math]C_{ij}[/math] следует рассмотреть два случая. В первом случае, когда [math]D_{j} = d_{ij}[/math] ([math]i[/math]-й объект является медоидом [math]j[/math]-го объекта) может быть два варианта: [math]E_{j} \lt = d_{jh}[/math] (медоидом [math]j[/math]-го объекта станет второго ближайший к нему медоид), тогда справедливо равенство [math]T_{ijh} = E_{j} - D_{j}[/math] и [math]E_{j} \gt d_{jh}[/math] (медоидом [math]j[/math]-го объекта станет [math]h[/math]-й объект), тогда справедливо равенство [math]T_{ijh} = d_{jh} - D_{j}[/math]. Во втором случае, когда [math]D_{j} != d_{ij}[/math] ([math]i[/math]-й объект НЕ является медоидом [math]j[/math]-го объекта) также может быть два варианта: [math]D_{j} \lt = d_{jh}[/math] (медоид [math]j[/math]-го объекта не изменится), тогда справедливо равенство [math]T_{ijh} = 0[/math] и [math]D_{j} \gt d_{jh}[/math] (медоидом [math]j[/math]-го объекта станет [math]h[/math]-й объект), тогда справедливо равенство [math]T_{ijh} = d_{jh} - D_{j}[/math]. Таким образом, в первом случае ([math]i[/math]-й объект является медоидом [math]j[/math]-го объекта) значение [math]T_{ijh}[/math] может быть вычислено по формуле [math]T_{ijh} = min(E_{j}, d_{jh}) - D_{j}[/math], а во втором ([math]i[/math]-й объект НЕ является медоидом [math]j[/math]-го объекта) – по формуле [math]T_{ijh} = min(d_{jh} - D_{j}, 0)[/math]. В формулах выше [math]min(x, y)[/math] – это операция получения минимального из двух значений [math]x[/math] и [math]y[/math].
1.5 Схема реализации последовательного алгоритма
В соответствии с математическим описанием алгоритм включает две стадии BUILD и SWAP. Рассмотрим реализацию каждой стадии. При описании реализации последовательного алгоритма на псевдокоде будем считать, что в программе поддерживаются следующие переменные:
[math]d_{ij}[/math] – расстояние между [math]i[/math]-м и [math]j[/math]-м объектами [math]K[/math] – требуемое число кластеров [math]O[/math] – множество всех объектов [math]S[/math] – множество медоидов [math]U[/math] – множество всех объектов, кроме медоидов [math]U = O - S[/math] [math]D_{i}[/math] – расстояние от [math]i[/math]-го объекта до его медоида [math]E_{i}[/math] – расстояние от [math]i[/math]-го объекта до второго ближайшего к нему медоида
Значения [math]D_{i}[/math] и [math]E_{i}[/math] необходимо поддерживать для вычисления значений [math]C_{ij}[/math] и [math]T_{ijh}[/math].
Реализация стадии BUILD:
Найти первый медоид [math]m[/math] как [math]arg\min_{i \in U} \sum_{j \in U} d_{ij}[/math] Инициализировать [math]S[/math] как множество из одного объекта [math]m[/math] Инициализировать [math]U[/math] как множество всех объектов, кроме объекта [math]m[/math] Выполнить тело цикла [math]K-1[/math] раз Начало тела цикла Найти следующий медоид [math]m[/math] как [math]arg\max_{i \in U} \sum_{j \in U - \{i\}} C_{ij}[/math] Добавить к [math]S[/math] объект [math]m[/math] Убрать из [math]U[/math] объект [math]m[/math] Конец тела цикла
Реализация стадии SWAP:
Инициализировать флаг продолжить_счёт значением истина
Выполнить цикл с предусловием пока флаг продолжить_счёт имеет значение истина
Начало тела цикла
Вычислить значения [math]D_{i}, E_{i}[/math] для всех объектов из множества [math]U[/math]
Вычислить пару [math]i[/math] и [math]h[/math]: [math]arg\min_{i \in S, h \in U} \sum_{j \in U + \{i\}} T_{ijh}[/math]
Если [math]\sum_{j \in U + \{i\}} T_{ijh} \lt 0[/math], то выполнить обмен:
Добавить в [math]S[/math] объект [math]h[/math] и убрать объект [math]i[/math]
Добавить в [math]U[/math] объект [math]i[/math] и убрать объект [math]h[/math]
Иначе
Присвоить флагу продолжить_счёт значением ложь
Конец тела цикла
Реализация алгоритма в соответствии с данной схемой доступа на github[3].
1.6 Последовательная сложность алгоритма
При описании последовательной сложности будем считать, что выполняется распределение [math]N[/math] объектов по [math]K[/math] кластерам. В соответствии с приведённым математическим описанием алгоритм включает в себя подготовительную стадию BUILD и итерационную стадию SWAP.
Стадия BUILD сводится к вычислению:
Одной операции [math]arg\min_{i} \sum_{j} d_{ij}[/math] [math]K-1[/math] операций [math]arg\max_{i \in U} \sum_{j \in U - \{i\}} C_{ij}[/math]
Т.е. стадия BUILD требует:
[math]K * N^2[/math] операций сложения [math]K * N[/math] операций сравнения (определения максимума/минимума) Около [math]K * N^2[/math] вычислений [math]C_{ij}[/math]
Одна итерация стадии SWAP сводится к вычислению:
[math]arg\min_{i \in S, h \in U} \sum_{j \in U + \{i\}} T_{ijh}[/math]
Т.е. одна итерации стадии SWAP требует порядка:
[math]K * N^2[/math] операций сложения [math]K * N[/math] операций сравнения (определения максимума/минимума) [math]K * (N - K) * (N - K - 1)[/math] вычислений [math]T_{ijh}[/math]
Вычисления [math]C_{ij}[/math] и [math]T_{ijh}[/math] имеют константную сложность для любых [math]i[/math], [math]j[/math] и [math]h[/math], поэтому сложность одной итерации алгоритма определяется как [math]O(K * N^2)[/math]. Таким образом можно отнести алгоритм PAM к алгоритмам с квадратичной сложностью по количеству [math]N[/math] объектов.
1.7 Информационный граф
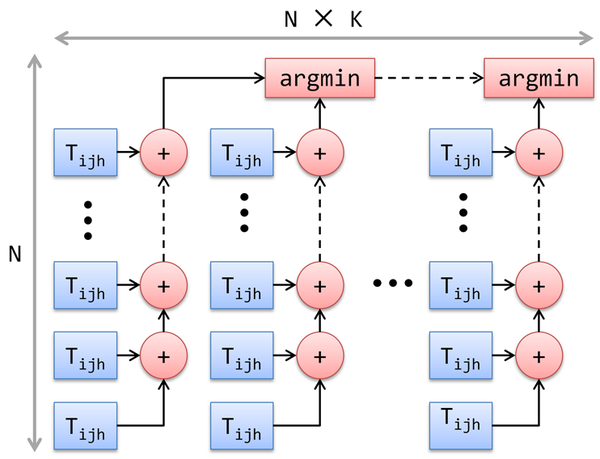
На рисунке 1.7.1 показан информационный граф для итерации стадии SWAP. Опишем его аналитически. Нетрудно видеть, что граф состоит из [math]K * N[/math] групп, представляющих собой сумму [math]N[/math] элементов. Суммы из разных групп не связаны между собой и в следствие этого могут быть вычислены параллельно на разных ядрах. Данное свойство хорошо отражает параллельную структуру алгоритма.
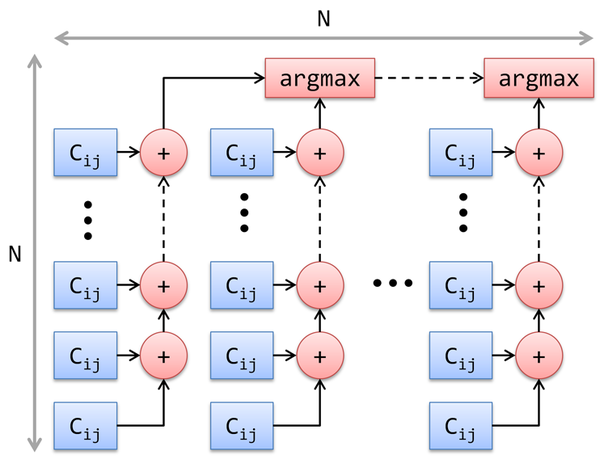
На рисунке 1.7.2 показан информационный граф для выбора медоида на стадии BUILD. Его описание практически полностью совпадает с описанием графа для итерации стадии SWAP, за исключением того, что он содержит всего [math]N[/math] групп сумм [math]N[/math] элементов.
1.8 Ресурс параллелизма алгоритма
Исходя из предположения неограниченности ресурсов будем считать, что в нашем распоряжении имеется [math]N * K[/math] вычислительных ядер, память каждого из которых целиком содержит матрицу расстояния [math]D[/math].
Стадия BUILD состоит из выбора начального (центрального) медоида и выбора [math]K - 1[/math] оставшихся медоидов. Для выбора медоида требуется вычисления [math]arg\max_{i \in U} \sum_{j \in U - \{i\}} C_{ij}[/math] ([math]arg\min_{i \in U} \sum_{j \in U} d_{ij}[/math]) для всех не выбранных объектов (из множества [math]U[/math]). Сумму в операции [math]arg\max[/math] ([math]arg\min[/math]) можно считать независимо на разных ядрах, поэтому сложность выбора одного медоида на стадии BUILD можно сократить с [math]O(N^2)[/math] до [math]O(N)[/math] (сложность вычисления суммы на одном ядре). Выбор одного медоида на стадии BUILD осуществляется [math]K[/math] раз, следовательно, сложность параллельной реализации стадии BUILD (в соответствии с данным описанием) будет равна [math]O(K * N)[/math]. Также стоит отметить, что для выполнения стадии BUILD описанным выше образом, достаточно задействовать лишь [math]N[/math] вычислительных ядер, а не [math]N * K[/math].
Проведём аналогичные рассуждения для одной итерации стадии SWAP. Выполнение одной итерации требует вычисления [math]arg\min_{i \in S, h \in U} \sum_{j \in U + \{i\}} T_{ijh}[/math] для каждой пары медоида и объекта. Сумму в операции [math]arg\min[/math] можно считать независимо на разных ядрах, поэтому сложность одной итерации стадии SWAP можно сократить с [math]O(K * N^2)[/math] до [math]O(N)[/math] если задействовать [math]N * K[/math] вычислительных ядер. Если в нашем распоряжении есть только [math]N[/math] вычислительных ядер, то сложность операции одной итерации стадии SWAP будет равна [math]O(K * N)[/math].
В результате проведённых рассуждений можно сделать вывод о том, что сложность параллельной реализации алгоритма является линейной по числу объектов кластеризации [math]O(K * N)[/math] против квадратичной сложности [math]O(K * N^2)[/math] в последовательном случае.
Выполнение стадии BUILD состоит из [math]K[/math] шагов.
Выполнение шага с номером [math]Step = 1,2,...,K[/math] включает следующие ярусы канонической ярусно-параллельной формы:
При [math]Step = 1[/math]: 1. [math]N - 1[/math] операций сложения 2. [math]N - 1[/math] операций минимума двух чисел
Максимальная ширину равную [math]N[/math] имеет 1 ярус.
При [math]Step \gt 1[/math]: 1. [math]N - Step[/math] операций вычитания 2. [math]N - Step[/math] операций максимума 3. [math]N - Step[/math] операций сложения 4. [math]N - Step[/math] операций максимума 5. Добавление нового медоида (не требует выполнения рассматриваемых операций)
Максимальную ширину равную [math]N - Step + 1[/math] имеют ярусы 1, 2 и 3.
Таким образом, параллельная сложность стадии BUILD включает:
[math]2*N*K - K^2 - N - K + 1[/math] операций сложения (вычитания) [math]2*N*K - K^2 - N - K + 1[/math] операций максимума (минимума)
Выполнение одной итерации стадии SWAP включает следующие ярусы канонической ярусно-параллельной формы:
1. [math]N - K + 1[/math] операций минимума 2. [math]N - K + 1[/math] операций вычитания 3. [math]N - K[/math] операций сложения 4. [math]K * (N - K) - 1[/math] операций минимума 5. Выполнение операции обмена (не требует выполнения рассматриваемых операций)
Максимальную ширину равную [math]K * (N - K)[/math] имеют ярусы 1, 2 и 3.
Таким образом, параллельная сложность стадии SWAP включает:
[math]2*N - 2*K + 1[/math] операций сложения (вычитания) [math]N*K + N - K + 1[/math] операций максимума (минимума)
1.9 Входные и выходные данные алгоритма
Входные данные:
1. Матрица расстояния (в смысле непохожести) между объектами кластеризации (dissimilarity matrix) [math]D[/math] (элементы [math]d_{ij}[/math]). Дополнительные ограничения: [math]D[/math] – симметрическая матрица порядка [math]N[/math], т.е. [math]d_{ij}= d_{ji}, i, j = 1, \ldots, N[/math] [math]D[/math] – содержит нули на главной диагонали, т.е. [math]d_{ii}= 0, i = 1, \ldots, N[/math] 2. [math]K[/math] - число кластеров, на которое следует разбить объекты кластеризации
Объём входных данных:
[math]\frac{N (N - 1)}{2}[/math] (в силу симметричности и нулевой главной диагонали достаточно хранить только над/поддиагональные элементы). В разных реализациях эта экономия хранения может быть выполнена разным образом.
Выходные данные:
[math]N[/math] чисел [math]k_{1}, k_{2}, \ldots, k_{N}[/math], где [math]k_{i}[/math] - целое число, соответствующее кластеру [math]i[/math]-го объекта.
Выходными данными алгоритма также можно считать [math]K[/math] чисел, задающих номера объектов кластеризации, выделенных в качестве медоидов (medoids). Однако в большинстве случаев требуется именно определение кластеров объектов, а не поиск соответствующих медоидов.
Объём выходных данных:
[math]N[/math] (кластеры объектов)
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности в предположении о неограниченности ресурсов в описанном выше случае является линейным (отношение квадратичной сложности к линейной).
При описании вычислительной мощности будем считать, что для завершения работы алгоритма PAM требуется выполнить [math]Q[/math] итераций стадии SWAP.
Последовательная вычислительная мощность как стадии BUILD так и одной итерации стадии SWAP равна [math]O(K)[/math]. Следовательно, последовательная вычислительная мощность алгоритма равна [math]O(Q * K)[/math].
Параллельная вычислительная мощность стадии BUILD и одной итерации стадии SWAP, в случае когда используется [math]N[/math] вычислительных узлов, равна [math]O(\frac{K}{N})[/math]. В случае когда используется [math]N * K[/math] вычислительных узлов для одной итерации стадии SWAP это значение снижается до [math]O(\frac{1}{N})[/math]. Следовательно, параллельная вычислительная мощность алгоритма равна [math]O(\frac{Q * K}{N})[/math], в случае когда используется [math]N[/math] вычислительных узлов, и [math]O(\frac{Q + K}{N})[/math], в случае когда используется [math]N * K[/math] вычислительных узлов.
| Вычислительная мощность | Последовательной реализации | Параллельной реализации ([math]N[/math] вычислительных узлов) |
Параллельной реализации ([math]N * K[/math] вычислительных узлов) |
|---|---|---|---|
| Стадии BUILD | [math]O(K)[/math] | [math]O(\frac{K}{N})[/math] | [math]O(\frac{K}{N})[/math] |
| Одной итерации стадии SWAP | [math]O(K)[/math] | [math]O(\frac{K}{N})[/math] | [math]O(\frac{1}{N})[/math] |
| Алгоритма PAM | [math]O(Q * K)[/math] | [math]O(\frac{Q * K}{N})[/math] | [math]O(\frac{Q + K}{N})[/math] |
Основные достоинства алгоритма PAM:
- Менее чувствителен к выбросам, чем алгоритм [math]k[/math]-средних
- Достаточно прост с точки зрения реализации
- Устойчив, поскольку не накапливает ошибок в процессе своей работы
- Возможно распараллеливание
Основные недостатки алгоритма PAM:
- Необходимо задание требуемого числа кластеров
- Квадратичная вычислительная сложность
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Для исследования масштабируемости алгоритма PAM использовалась доступная на github[4] реализация алгоритма. Исследование проводилось на суперкомпьютере BlueGene/P[5].
Были измерено время выполнения для каждой из двух, составляющих всю программу, частей:
- Чтение и подготовка исходных данных
- Выполнение алгоритма PAM
Для проведения измерений было подготовлено 6 наборов псевдослучайных данных, содержащих от 1024 до 6144 (с шагом 1024) объектов кластеризации. Измерения проводились для числа процессов равного 1 и кратного 4 в диапазоне от 1 до 256: 1, 4, 8, 16, ..., 252, 256.
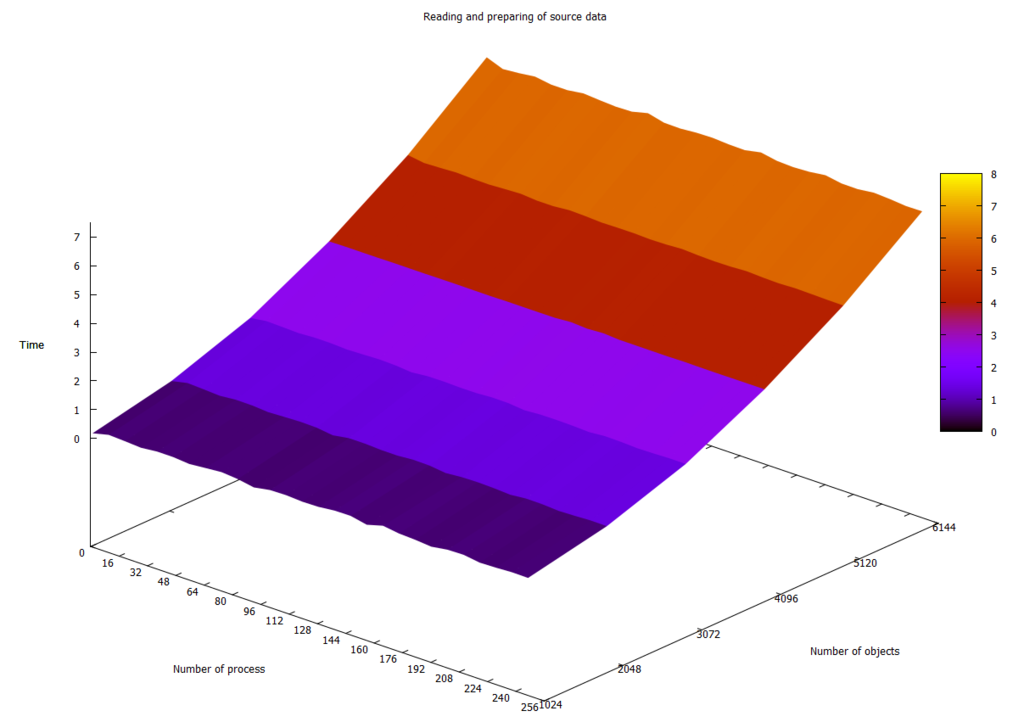
На рисунке 2.4.1 показана зависимость времени чтения и подготовки исходных данных от числа процессов и размера данных. График наглядно демонстрирует, что данное время в исследуемой реализации зависит лишь от объёма данных, но не от числа процессов. Также можно заметить небольшие шероховатости на графике, свидетельствующие о том, что данное время может незначительно изменяться от запуска к запуску.
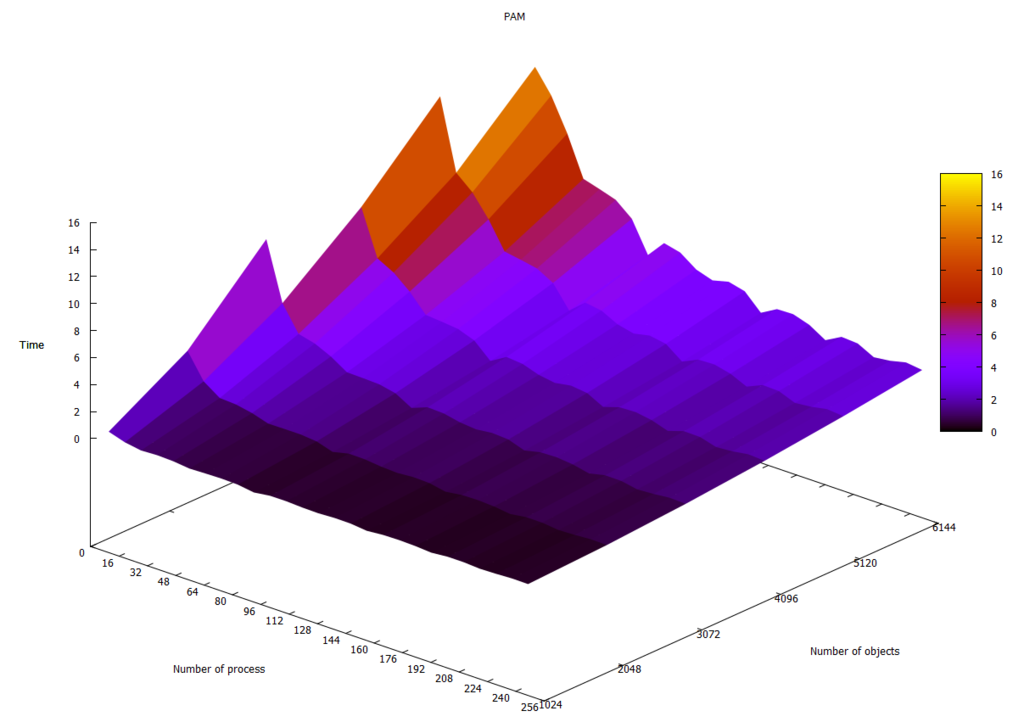
На рисунке 2.4.2 показана зависимость времени работы алгоритма PAM от числа процессов и размера данных. График иллюстрирует хорошую масштабируемость алгоритма в случае, когда число объектов кластеризации превышает число процессов.
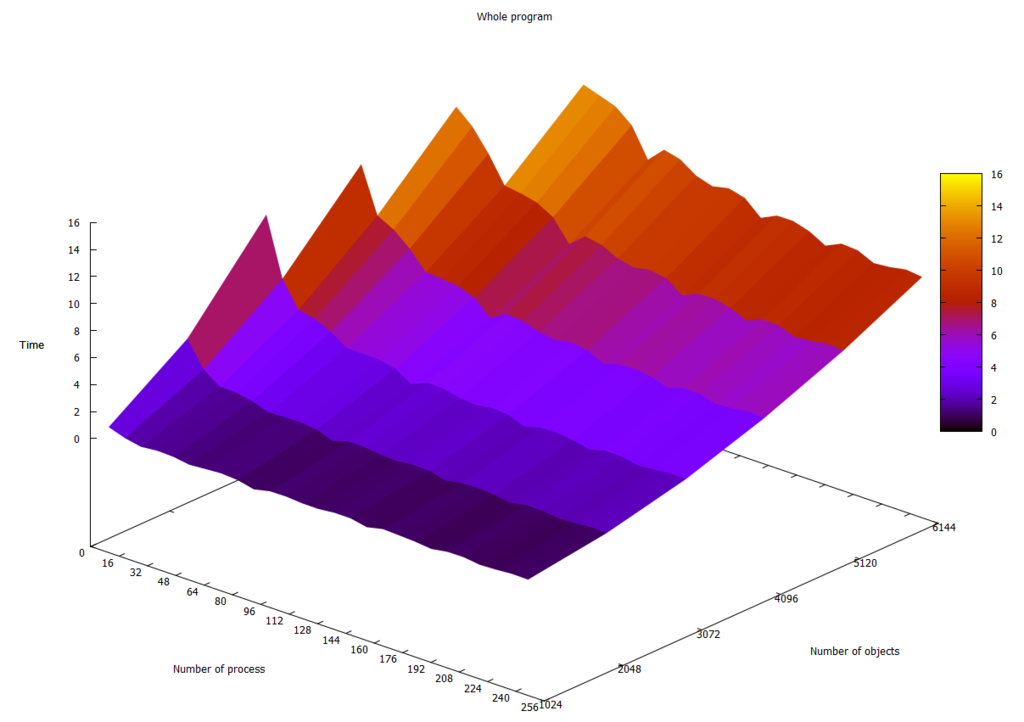
На рисунке 2.4.3 показана зависимость общего времени работы программы от числа процессов и размера данных. Заметно ухудшение масштабируемости по сравнению с графиком на рисунке 2.4.2.
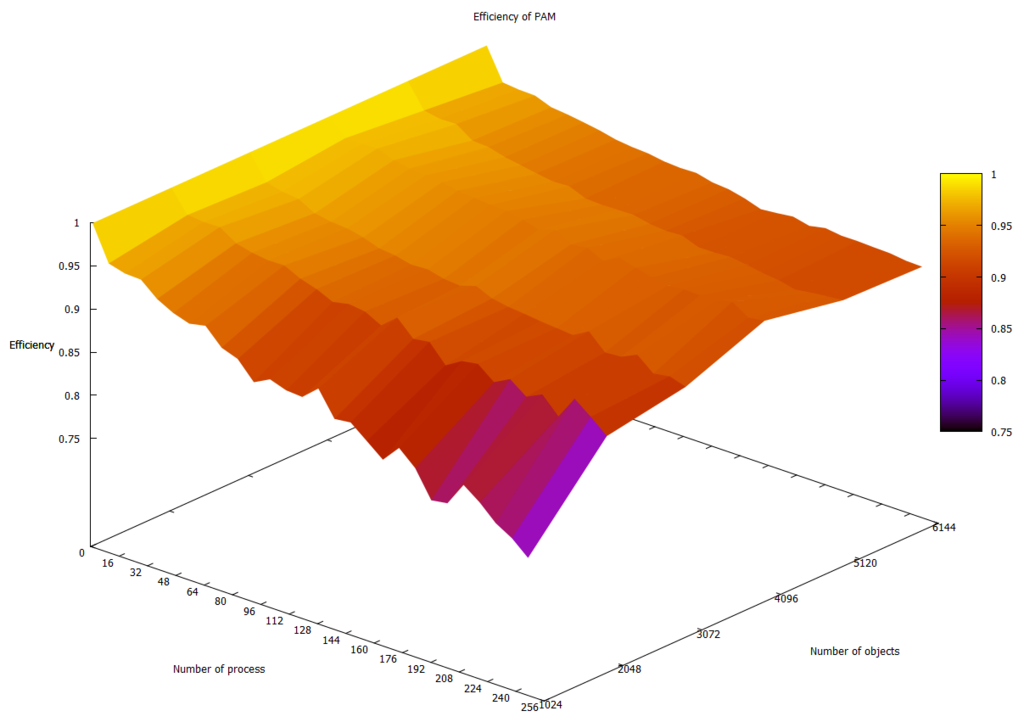
На рисунке 2.4.4 показана зависимость эффективности алгоритма PAM от числа процессов и размера данных. График показывает, что эффективность снижается не очень быстро с ростом числа процессов, что также иллюстрирует хорошую масштабируемость алгоритма в случае, когда число объектов кластеризации превышает число процессов.
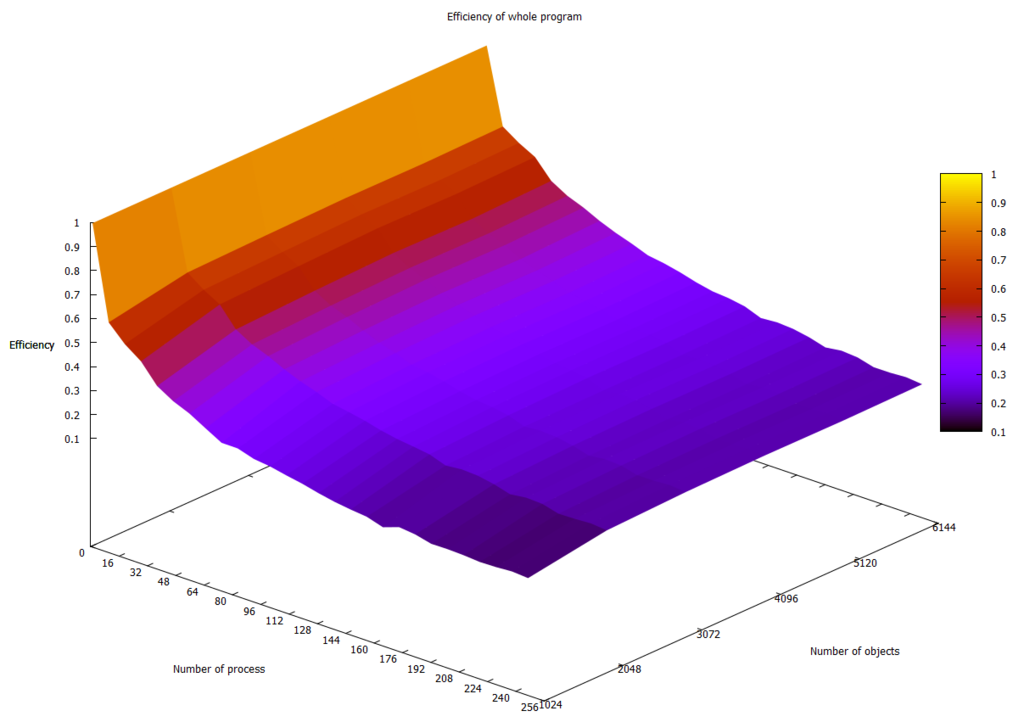
На рисунке 2.4.5 показана зависимость эффективности работы всей программы от числа процессов и размера данных. Заметно ухудшение по сравнению с графиком на рисунке 2.4.4, за счёт добавления времени чтения и подготовки исходных данных. Эффективность заметно падает, с ростом числа процессов: время чтения и подготовки исходных данных остаётся неизменным, а время работы алгоритма PAM не даёт ускорения поскольку оно значительно меньше, чем время чтения и подготовки исходных данных (начиная с определённого числа процессов).
Масштабируемость рассматриваемой реализации алгоритма PAM:
- При увеличении числа процессов общая эффективность программы уменьшается, т.к. время чтения и подготовки исходных данных остаётся неизменным и начинает преобладать над временем работы алгоритма PAM.
- При увеличении числа объектов кластеризации общая эффективность программы постепенно увеличивается, т.к. время чтения и подготовки исходных данных растёт медленнее, чем время работы алгоритма PAM.
- При одновременном увеличении как числа процессов, так и числа объектов кластеризации общая эффективность программы уменьшается.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
- Последовательная реализация алгоритма PAM в пакете ClusterR на языке R:
- Лицензия: MIT
- веб-страница фреймворка (исходный код, системные требования и справочное руководство)
- Алгоритм PAM реализован в функции 'Cluster_Medoids'. Отличительная особенность реализации [2]:
- для задания метрики между элементами кластеризуемого множества передаётся строка, задающая одну из реализованных в алгоритме метрик. Данный подход теряет одно из преимуществ алгоритма PAM, позволяющее в качестве матрицы расстояний использовать произвольную матрицу различий.
- Последовательная реализация алгоритма PAM в пакете Cluster на языке R:
- Лицензия: GPL (≥2)
- веб-страница фреймворка (исходный код, системные требования и справочное руководство)
- Алгоритм PAM реализован в функции 'pam()'. Данная реализация имеет следующие особенности [3]:
- функция может принимать на вход не множество точек, а матрицу расстояний между ними;
- реализация более гибкая, так как принимает на вход матрицу различий элементов, а не использует какую-либо метрику;
- может быть предоставлено графическое отображение.
- Параллельная реализация алгоритма PAM в пакете SPRINT (Simple Parallel R INTerface - параллельный фреймворк) на языке R:
- Лицензия: GPL (≥3)
- веб-страница фреймворка (исходный код, системные требования и справочное руководство)
- Алгоритм PAM реализован в фукции 'ppam()'. Входные параметры данной функции схожи с параметрами, задаваемыми в линейной реализации 'pam()' пакета Cluster языка R. Отличительной особенностью является подача на вход предвычисленной матрицы расстояний (например, с помощью функции 'pcor()' из этой же библиотеки).[4]
- Параллельная реализация алгоритма PAM на основе операций MapReduce на Hadoop кластере.
- В рамках исследования по ускорению анализа информации о геноме были созданы реализации алгоритма PAM с использованием технологии MPI и технологии MapReduce. Реализация в открытом досупе отсутствует. [5]
3 Литература
- ↑ Kaufman, L. and P.J. Rousseeuw, Clustering by means of medoids, in: Y. Dodge (Ed.), Statistical Data Analysis based on the L1 Norm (North-Holland, Amsterdam, 1987) 405 — 416.
- ↑ Lampros Mouselimis Package 'ClusterR'. October 8, 2016
- ↑ Martin Maechler., etc. Package 'cluster'. October 8, 2016
- ↑ University of Edinburgh SPRINT Team. Package 'sprint'. February 20, 2015
- ↑ [Dobrzelecki B. et al. Managing and analysing Genomic Data using HPC and Clouds //Grid and Cloud Database Management. – Springer Berlin Heidelberg, 2011. – С. 261-277.