Участник:Мязина Екатерина/Алгоритм концептуальной кластеризации COBWEB

COBWEB
Последовательный алгоритм
Последовательная сложность	[math]log_{B}n*B^{2}AV[/math]

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Задача кластеризации – частный случай задачи обучения без учителя, которая сводится к разбиению имеющегося множества объектов данных на подмножества таким образом, что элементы одного подмножества существенно отличались по некоторому набору свойств от элементов всех других подмножеств. Объект данных обычно рассматривается как точка в многомерном метрическом пространстве, каждому измерению которого соответствует некоторое свойство (атрибут) объекта, а метрика – есть функция от значений данных свойств. Кластерный анализ выполняет следующие основные задачи:

• разработка типологии или классификации.
• исследование полезных концептуальных схем группирования объектов.
• порождение гипотез на основе исследования данных.
• проверка гипотез или исследования для определения, действительно ли типы (группы), выделенные тем или иным способом, присутствуют в имеющихся данных.

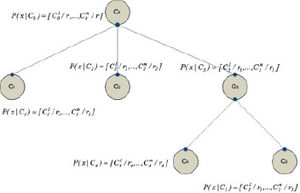
Для решения многих практических задач в настоящее время используется концептуальная кластеризация данных, ярким представителем которой является метод COBWEB. Алгоритм COBWEB – классический метод инкрементальной концептуальной кластеризации. Он создаёт иерархическую кластеризацию в виде дерева классификации: каждый узел этого дерева ссылается на концепт и содержит вероятностное описание этого концепта, которое включает в себя вероятность принадлежности концепта к данному узлу и условные вероятности вида: [math]{\displaystyle P(A_{j}=u_{ij}|C_{k})}[/math], где [math]{\displaystyle A_{j}}[/math] = [math]{\displaystyle u_{ij}}[/math] – пара атрибут-значение, [math]{\displaystyle C_{k}}[/math] – класс концепта. Узлы, находящейся на определённом уровне дерева классификации, называют срезом. Алгоритм использует для построения дерева классификации эвристическую меру оценки, называемую полезностью категории – прирост ожидаемого числа корректных предположений о значениях атрибутов при знании об их принадлежности к определённой категории относительно ожидаемого числа корректных предположений о значениях атрибутов без этого знания. Чтобы встроить новый объект в дерево классификации, алгоритм COBWEB итеративно проходит всё дерево в поисках «лучшего» узла, к которому отнести этот объект. Выбор узла осуществляется на основе помещения объекта в каждый узел и вычисления полезности категории получившегося среза. Также вычисляется полезность категории для случая, когда объект относится к вновь создаваемому узлу. В итоге объект относится к тому узлу, для которого полезность категории больше.

1.2 Математическое описание алгоритма

Пусть [math]{\displaystyle X}[/math] — множество объектов, [math]{\displaystyle Y}[/math] — множество номеров (имён, меток) кластеров. Задана функция расстояния между объектами [math]{\displaystyle \rho (x,x')}[/math]. Имеется конечная обучающая выборка объектов [math]{\displaystyle X^{m}=\{x_{1},\dots ,x_{m}\}\subset X}[/math]. Требуется разбить выборку на непересекающиеся подмножества, называемыекластерами, так, чтобы каждый кластер состоял из объектов, близких по метрике [math]{\displaystyle \rho }[/math], а объекты разных кластеров существенно отличались. При этом каждому объекту [math]{\displaystyle x_{i}\in X^{m}}[/math] приписывается номер кластера[math]{\displaystyle y_{i}}[/math]. Алгоритм кластеризации — это функция [math]{\displaystyle a\colon X\to Y}[/math], которая любому объекту [math]{\displaystyle x\in X}[/math] ставит в соответствие номер кластера [math]{\displaystyle y\in Y}[/math]. Множество [math]{\displaystyle Y}[/math] в некоторых случаях известно заранее, однако чаще ставится задача определить оптимальное число кластеров, с точки зрения того или иного критерия качества кластеризации.

В алгоритме COBWEB реализовано вероятностное представление категорий. Принадлежность категории определяется не набором значений каждого свойства объекта, а вероятностью появления значения. Например, [math]{\displaystyle P(A_{j}=u_{ij}|C_{k})}[/math] - это условная вероятность, с которой свойство [math]{\displaystyle A_{j}}[/math], принимает значение [math]{\displaystyle u_{ij}}[/math], если объект относится к категории [math]{\displaystyle C_{k}}[/math]. Для каждой категории в иерархии определены вероятности вхождения всех значений каждого свойства. При предъявлении нового экземпляра система COBWEB оценивает качество отнесения этого примера к существующей категории и модификации иерархии категорий в соответствии с новым представителем. Критерием оценки качества классификации является полезность категории (category utility). Критерий полезности категории был определен при исследовании человеческой категоризации. Он учитывает влияние категорий базового уровня и другие аспекты структуры человеческих категорий. Критерий полезности категории максимизирует вероятность того, что два объекта, отнесенные к одной категории, имеют одинаковые значения свойств и значения свойств для объектов из различных категорий отличаются. обозначим через – множество распознаваемых объектов, характеризуемое бинарными параметрами , принимаемыми одно из возможных значений . – множество формируемых кластеров, где n – заранее неизвестно. Полезность кластеризации в методе COBWEB рассматривается как функция [math]{\displaystyle CU}[/math], определяющая сходство объектов в рамках одного кластера, и их различие по отношению к объектам из других кластеров. Внутриклассовое сходство определяется условной вероятностью , а межклассовое сходство условной вероятностью . Функция полезности кластеризации определяется в виде [math]{\displaystyle CU= \frac{\sum_{k=1}^{N}P(A=u_{ij}|C_{k})\sum_{j}\sum_{i}(P(C_{k}|A=u_{ij})^2-P(A=u_{ij})^2)}{N}}[/math], где N – количество кластеров.

1.3 Вычислительное ядро алгоритма

Метод COBWEB строит дерево классификации с вероятностными описаниями концептов. Выбор возможного способа кластеризации объектов основан на значениях функции полезности кластеризации. При построении дерева классификации используются следующие 4 операции:

• отнесение объекта к наилучшему из существующих кластеров
• добавление нового кластера, содержащего единственный объект
• слияние двух существующих кластеров в один новый с добавлением в нее этого объекта
• разбиение существующего кластера на два и отнесение объекта к лучшему из вновь созданных кластеров

Модель концептуальной кластеризации

Пошаговое описание метода концептуальной кластеризации:

1. Вводится корневой кластер [math]{\displaystyle C_{0}}[/math], свойства которого совпадают со свойствами первого объекта [math]{\displaystyle O_{1}}[/math]=[math]{\displaystyle V_{11},\dots, V_{1m}}[/math]. Для каждого последующего объекта [math]{\displaystyle O_{i}}[/math]=[math]{\displaystyle V_{i1},\dots, V_{im}}[/math] выполняется цикл, реализующий шаги 2‒6, в рамках которых выполняются 4 выше представленные операции.
2. Объект [math]{\displaystyle O_{i}}[/math] добавляется поочередно в кластеры [math]{\displaystyle C_{1}}[/math], [math]{\displaystyle C_{2}}[/math],…, [math]{\displaystyle C_{k}}[/math]. После каждого добавления вычисляется полезность кластеризации [math]{\displaystyle CU_{1},\dots, CU_{k}}[/math].
3. Для объекта [math]{\displaystyle O_{i}}[/math] создается новый кластер [math]{\displaystyle C_{k+1}}[/math], объект помещается в кластер и вычисляется полезность кластеризации [math]{\displaystyle CU_{k+1}}[/math].
4. Объединяются два кластера с максимальными значением полезности кластеризации из [math]{\displaystyle CU_{1},\dots, CU_{k}}[/math]. Образуется новый кластер, в него добавляется объект [math]{\displaystyle O_{i}}[/math]. Вычисляется полезность кластеризации [math]{\displaystyle CU_{k+2}}[/math].
5. Объект [math]{\displaystyle O_{i}}[/math] добавляется в кластер с максимальным значением полезности кластеризации из [math]{\displaystyle CU_{1},\dots, CU_{k}}[/math]. Образуется новый кластер с двумя кластерами-потомками. Вычисляется полезность кластеризации [math]{\displaystyle CU_{k+3}}[/math].
6. Выбирается максимальное значение полезности кластеризации среди полезностей [math]{\displaystyle CU_{1},\dots, CU_{k}, CU_{k+1}, CU_{k+2}, CU_{k+3}}[/math], в соответствии с ним выбирается операция разбиения объектов по кластерам.

1.4 Макроструктура алгоритма

Макроструктура алгоритма представлена итеративным вызовом вычислительного ядра для каждого элемента из входного набора данных с уточнением дерева кластеризации на каждом шаге.

1.5 Схема реализации последовательного алгоритма

COBWEB(root, record):
  Input: A COBWEB node root, an instance to insert record
  if root has no children then
    children := {copy(root)}
    newcategory(record) \\ adds child with record’s feature values.
    insert(record, root) \\ update root’s statistics
  else
    insert(record, root)
    for child in root’s children do
      calculate Category Utility for insert(record, child),
      set best1, best2 children w. best CU.
    end for
    if newcategory(record) yields best CU then
      newcategory(record)
    else if merge(best1, best2) yields best CU then
      merge(best1, best2)
      COBWEB(root, record)
    else if split(best1) yields best CU then
      split(best1)
      COBWEB(root, record)
    else
      COBWEB(best1, record)
    end if
  end

1.6 Последовательная сложность алгоритма

Пусть [math]{\displaystyle B}[/math] - среднее число потомков узлов в дереве классификации и [math]{\displaystyle n}[/math] - число уже классифицированных объектов, тогда [math]{\displaystyle log_{B}n}[/math] - оценка глубины дерева классификации. Кроме того, положим [math]{\displaystyle A}[/math] равным числу свойств у классифицируемых объектов, а [math]{\displaystyle V}[/math] - среднее число значений, которые могу принимать данные свойства. В ходе определения к каком у классу отнести каждый следующий объект из входного набора, необходимо рассчитать значение функции полезности категории. Сложность расчета данной функции есть [math]{\displaystyle O(BAV)}[/math] и данное действие необходимо повторить для каждого из B потомков (в среднем). Кроме того, для классификации нам необходимо пройти по дереву, имеющему глубину [math]{\displaystyle log_{B}n}[/math], таким образом мы имеем оценку по сложности [math]{\displaystyle O(log_{B}n*B^{2}AV)}[/math].

1.7 Информационный граф

Для выполнения каждой итерации алгоритма (добавления очередного элемента в дерево классификации) необходимо иметь доступ по всему текущему состоянию дерева классификации. Однако, внутри шага алгоритма наблюдается полная независимость по данным. Имеется возможность произвести расчет функции полезности для каждого кластера независимо и в конце сравнить их значения.

1.8 Ресурс параллелизма

Основной вычислительной нагрузкой алгоритма является вычисление функции полезности для категорий. Однако, именно эта часть алгоритма поддается простому и логичному распараллеливанию. Можно выделить два пути к получению параллельной версии исходного алгоритма:

• распараллеливание вычисления каждой конкретной функции полезности
• распараллеливание процесса вычисления совокупности функций полезности

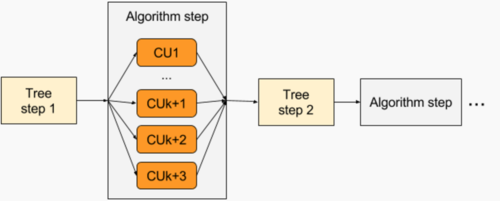
В первом случае предлагается распараллелить цикл вычисления суммы, являющийся основой функции полезности. Второй подход предлагает распараллелить процесс более высокоуровнево. Из описания ядра алгоритма видно, что для добавления каждого элемента в дерево необходимо вычислить [math]{\displaystyle k+3}[/math] раза функцию полезности. Стоит заметить, что вычисления функции полезности никак не зависят друг от друга и могут быть выполнены параллельно.

Кроме того, стоит отметить, что оба данных подхода к распараллеливанию могут быть использованы вместе, что может быть полезно на системах типа MPI+OpenMP.

С точки зрения простоты реализации и получения наибольшей выгоды второй подход является более привлекательным и позволяет избавиться от квадратичной сложности, понизив оценку до [math]log_{B}n*BAV[/math].

1.9 Входные и выходные данные алгоритма

На вход алгоритм принимает множество объектов, характеризуемых набором свойств. В свою очередь, каждое свойство может принимать какое-либо значение из множества допустимых значений. Результатом работы алгоритма является построенное дерево классификации, листья которого представляют собой различные классы объектов и содержат сами объекты принадлежащие данному классу.

2 Программная реализация алгоритма

2.7 Существующие реализации алгоритма

• Working python implementation of COBWEB