Участник:Пискунов Константин/ Алгоритм кластеризации категориальных данных (Clustering with sLOPE, CLOPE)

Алгоритм CLOPE
Последовательный алгоритм
Последовательная сложность	[math]O(N*k*A)[/math]
Объём входных данных	[math]N*A+1[/math]
Объём выходных данных	[math]N[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(N*A)[/math]
Ширина ярусно-параллельной формы	[math]O(N*k*A)[/math]

Основные авторы описания: К.А.Пискунов

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Задачи кластеризации больших массивов категорийных данных весьма актуальна для систем анализа данных. Категорийные данные встречаются в любых областях: производство, коммерция, маркетинг, медицина… Категорийные данные включают в себя и так называемые транзакционные данные: чеки в супермаркетах, логи посещений веб-ресурсов. Сюда же относится анализ и классификация текстовых документов (Text Mining).

Здесь и далее под категорийными данными понимаются качественные характеристики объектов, измеренные в шкале наименований. Напомним: при использовании шкалы наименований указывается только, одинаковы или нет объекты относительно измеряемого признака.

Алгоритм CLOPE. Предназначен для кластеризации огромных наборов категорийных данных. К достоинствам относятся высокие масштабируемость и скорость работы и качество кластеризации, что достигается использованием глобального критерия оптимизации на основе максимизации градиента высоты гистограммы кластера. Отличается простотой программной реализации. Во время работы алгоритм хранит в памяти небольшое количество информации по каждому кластеру и требует минимальное число сканирований набора данных. CLOPE автоматически подбирает количество кластеров, причем это регулируется одним единственным параметром коэффициентом отталкивания. CLOPE предложен в 2002 году группой китайских ученых . При этом он обеспечивает более высокую производительность и лучшее качество кластеризации в сравнении с многими иерархическими алгоритмами.

Во время работы в оперативной памяти хранится только текущая транзакция и небольшое количество информации по каждому кластеру, которая состоит из: количества транзакций N, числа уникальных объектов (или ширины кластера) W, простой хэш-таблицы для расчета Occ(i,C) и значения S площади кластера.

Во время работы алгоритм хранит в RAM небольшое количество информации по каждому кластеру и требует минимальное число сканирований набора данных. CLOPE автоматически подбирает количество кластеров, причем это регулируется одним единственным параметром – коэффициентом отталкивания.

В основе алгоритма кластеризации CLOPE лежит идея максимизации глобальной функции стоимости, которая повышает близость транзакций в кластерах при помощи увеличения параметра кластерной гистограммы

1.2 Математическое описание алгоритма

Пусть имеется база транзакций [math]D[/math], состоящая из множества транзакций [math]\{t_{1},t_{2},...,t_{n}\}[/math]. Каждая транзакция есть набор объектов [math]\{i_1,...,i_A\} [/math].

Множество кластеров [math]\{C_1,...,C_k\} [/math] есть разбиение множества [math]\{t_1,...t_n\} [/math], такое, что [math]C_1 \cup \ldots \cup C_k = \{t_1,...,t_n\}[/math] и [math]C_i[/math] [math]\ne[/math] [math]\empty[/math] [math]\land[/math] [math]C_i[/math] [math]\cap[/math] [math]C_j= \empty[/math], для [math]1[/math] [math]\le[/math] [math]i[/math], [math] j[/math] [math] \le[/math] [math] k[/math].

Каждый элемент [math] C_i[/math] называется кластером , [math] n[/math] — количество транзакций, [math]A [/math] — длина транзакции, [math]k [/math] — число кластеров.

При этом задан параметр [math]r[/math] - коэффициент отталкивания.

Характеристики кластера [math]C_j [/math] :

[math]D(C_j)[/math] — множество уникальных объектов;

[math]Occ(i,C_j) [/math] — количество вхождений объекта [math] i[/math] в кластер [math] C_j[/math] ;

[math]S(C_j) = \sum_{i \in D(C_j)} Occ(i,C_j) = \sum _{t_i \in C_j} \mid t_i \mid [/math]

[math]W(C_j) [/math]  =  [math] \mid[/math] [math]D(C_j)[/math] [math]\mid[/math] — высота кластера;

[math]H(C_j)[/math] = [math]S(C_j)[/math] [math]/[/math] [math]W(C_j)[/math] — ширина кластера.

Формула для вычисления глобального критерия — функции стоимости текущей кластеризации [math]C = \{C_1, \ldots C_k\}[/math], обозначаемой, как [math] Profit(C)[/math] :

[math] Profit(C)=\frac{\sum^{k}_{i=1} G(C_i) \times \mid C_i \mid} {\sum^{k}_{i=1} \mid C_i \mid} [/math]  =  [math]\frac{\sum^{k}_{i=1} \frac {S(C_i)}{{W(C_i)}^r} \times \mid C_i \mid} {\sum^{k}_{i=1} \mid C_i \mid} [/math]

Для построения начального распределения транзакций по кластерам необходимо сделать первый проход по таблице (фаза инициализации). В время нее для каждой транзакции выбирается кластер таким образом, чтобы функция [math] Profit(C)[/math] была максимальной.

Далее происходят "уточняющие" проходы (фаза итерации), где для каждой транзакции производится попытка перемещения в другой кластер так, чтобы [math] Profit(C) \longrightarrow max[/math].

Если больше не существует перемещений транзакций, увеличивающих глобальную стоимость [math] Profit(C) [/math], то действие алгоритма заканчивается.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма состоит в многократном вычислении цены добавления и удаления транзакции, которые выполняются на каждой итерации для каждой транзакции — выражения [math]Cost^{\pm}(C_i, t_n) = \frac{\overline{S} (C_i) * (|C_i| \pm 1)}{\overline{W}(C_i)^r} - \frac{S(C_i) * |C_i|}{W(C_i)^r}[/math]   (2 операции умножения, 2 операции деления, 2 возведения в степень и 1 инкремент/декремент)

1.4 Макроструктура алгоритма

Как записано в описании ядра алгоритма, основную часть метода составляют вычисление цены добавления/удаления транзакции.

В инициализации происходит распределение по кластерам, далее происходят итерации максимизирующие функцию стоимости и так происходит обход до тех пор, пока не перестанут происходить изменения.

1.5 Схема реализации последовательного алгоритма

Пусть поисковые профили хранятся в таблице базы данных. Для построения начального разбиения, определяемого функцией Profit(C,r) требуется первый проход по таблице профилей. После этого требуется незначительное (1-3) количество дополнительных сканирований таблицы для повышения качества кластеризации и оптимизации функции стоимости. Если в текущем проходе по таблице, изменений не произошло, то алгоритм прекращает свою работу. При построении начального разбиения из таблицы читается очередной профиль и создается новый кластер (отдельная таблица) или помещается в уже существующий кластер, который дает максимум Profit(C,r). На итерационном этапе просматривается таблица профилей и для каждого профиля решается задача определения кластера, если новый кластер максимизирует Profit(C,r), то профиль переносится в этот кластер. В начале каждого цикла устанавливается индикатор перемещения moved := false. Если в цикле происходит перемещение профиля индикатор перемещения изменяется moved :=true. Итерации завершаются, если значение moved=false не изменится. После завершения итераций удаляются все пустые кластеры.

1.6 Последовательная сложность алгоритма

Пусть средняя длина транзакции равна A, общее число транзакций N, максимально возможное число кластеров K. Временная сложность одной итерации равна O(N*K*A), (что вытекает из количества операций согласно описанию вычислительного ядра алгоритма), показывающая, что скорость работы алгоритма растет линейно с ростом кластеров и размера таблицы. Это делает алгоритм быстрым и эффективным на больших объемах.

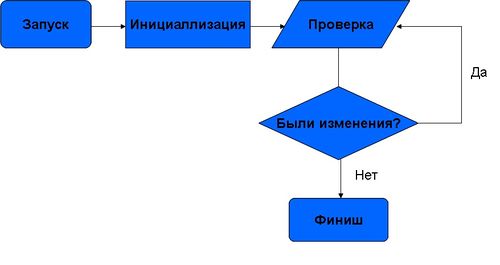
1.7 Информационный граф

На Рис.1 общая схема реализации алгоритма. На входе у нас имеется следующий набор: [math]N[/math] транзакций длины [math]A[/math] и коэффициент отталкивания [math]r[/math]. Во время "Инициаллизации" происходит распределение транзакций по кластерам. Далее происходит проверка до тех пор, пока происходят перемещения, ведущие к увеличению общей стоимости.

Рис.1. Общая схема CLOPE

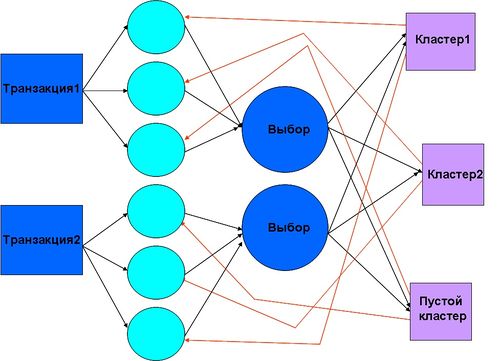
Подробнее рассмотрим стадию "Инициаллизации". В схематичном описании на Рис. 2 пара транзакций на входе, далее подсчет стоимости их добавления на один из кластеров или через пустой кластер осуществляется перемещение транзакций на новый кластер. Фаза с удалением транзакции с кластера включает еще и стоимость удаления, поэтому представлен граф только для добавления.

Рис.2. Cтадия "Инициаллизации"

1.8 Ресурс параллелизма алгоритма

Параллелизм возникает в момент вычисления цены добавления/удаления транзакции. Вычисление цены на разных кластерах не зависят друг от друга, значит могут выполняться параллельно. Количество транзакций алгоритма [math]N[/math], длина транзакции алгоритма — [math]A[/math], тогда сложность параллельного алгоритма будет [math]O(N*A)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные:

• набор из [math]N[/math] транзакций длины не более [math]A[/math] и коэффициент отталкивания [math]r[/math].

Объем входных данных:

• [math]N * A[/math] символов, строк или чисел (зависит от того, в каком виде представляются категории) и [math]1[/math] вещественное число..

Выходные данные:

• распределение исходного набора транзакций по кластерам.

Объем выходных данных:

• [math]N[/math] положительных целых чисел - номера кластеров, соответствующих каждой из транзакций.

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности является линейной: k.

При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – линейна.

Алгоритм не устойчив из-за того, что результат его работы зависит от начального распределения по кластерам. А так как алгоритм зависит от порядка обхода кластеров, то строго нельзя говорить и о его детерминированности.

В связи с ориентиром на категориальные данные, алгоритм не предназначен к работе с числами. (Большая разница в числах отнесет их к разным категориям.)

Обеспечивает более высокую производительность и лучшее качество кластеризации в сравнении с многими иерархическими алгоритмами.

К достоинствам относятся высокие масштабируемость и скорость работы и качество кластеризации, что достигается использованием глобального критерия оптимизации на основе максимизации градиента высоты гистограммы кластера.

Во время работы алгоритм хранит в RAM небольшое количество информации по каждому кластеру и требует минимальное число сканирований набора данных. CLOPE автоматически подбирает количество кластеров, причем это регулируется одним единственным параметром – коэффициентом отталкивания.

Количество итераций может быть задано пользователем, а может остаться не известным. Второе лучше отразится на качестве кластеризации, но не будет известно количество итераций.

2 Программная реализация алгоритма

2.2 Существующие реализации алгоритма

Поскольку алгоритм CLOPE является достаточно новым, то сейчас нет его массовой реализации, как и в отечественных, так и западных пакетах.

WEKA - библиотека алгоритмов машинного обучения и анализа данных на языке Java.

Имеются частные пользовательские реализации алгоритма.

Имеются публикации, посвященные данному алгоритму:

• Wang, K., Xu, C.. Liu, B. Clustering transactions using large items. In Proc. CIKM’99, Kansas, Missouri, 1999.

• Fasulo D. «An Analysis Of Recent Work on Clustering Algorithms». Department of Computer Science & Engineering.» / D. Fasulo// University of Washington,1999.