Участник:Abogovski/Вспомогательная задача при решении задачи Штурма-Лиувилля с условиями сопряжения
Боговский Антон, 409
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
К этой вспомогательной задаче (см. Математическое описание алгоритма) сводится решение задачи Штурма-Лиувилля с условия сопряжения, возникающей при разделении переменных в краевой задаче для эллиптического оператора с кусочно-постоянными коэффицентами. Ищутся области (углы) для которых, существуют собственное число равное единице.
1.1 Общее описание алгоритма
Искомые области находятся перебором параметров области (углы, на которых коэффицент постоянен, и значения коэффицента на этих подобластях.
1.2 Математическое описание алгоритма
Рассмотрим задачу Дирихле на ограниченной области для эллиптического уравнения в дивергентной форме с кусочно-постоянными коэффицентами. [math]div(\varkappa grad u) = div F [/math], где коэффицент [math]\varkappa[/math] -- кусочно-постоянный. При решении задачи методом разделения переменных в полярных возникает задача Штурма-Лиувилля относительного полярного угла [math]\Phi'(\varphi) = \lambda \Phi(\varphi)[/math] c условиями сопряжения на разрывах коэффицента: непрерывность [math]\Phi(\varphi)[/math] и [math]\varkappa(\varphi)\Phi'(\varphi)[/math].
В качестве области для модельной задачи возьмем круг (или сектор круга) с радиальными линиями разрыва [math]\varkappa(\varphi)[/math]. Тогда на каждом отрезке непрерывности [math]\varkappa(\varphi)[/math] решение -- линейная комбинация [math]cos(\sqrt{-\lambda}\varphi)[/math] и [math]sin(\sqrt{-\lambda}\varphi)[/math]. Если для области такого вида (набора значений [math]\varkappa[/math] и величин углов) существуют набор постоянных при [math]cos(\sqrt{-\lambda}\varphi)[/math] и [math]sin(\sqrt{-\lambda}\varphi)[/math], такой что граничные условия и условия сопряжения выполнены, то существует собственная функция.
Ищем такие области. Заметим, что решения задачи штурма Лиувилля зависят от [math]\alpha = \sqrt{-\lambda}\varphi[/math] -- перейдем к такой переменной. Зададим граничное условие на одной стороне сектора, условия сопряжения на линиях разрыва и проверим (переберем) различные значения [math]\alpha, \varkappa[/math] на выполнение граничного условия на правой стороне.
(Условия сопряжения дают связь между коэффицентами при [math]cos,sin[/math] через композицию матриц растяжения и поворота, зависящих от [math]\alpha, \varkappa[/math]).
1.3 Вычислительное ядро алгоритма
Перебор параметров. Можно рассматривать вычислительное как обход дерева всех наборов значений параметров.
- Для первой подобласти фиксируется значение [math]\varkappa=1[/math] и поддиапазон перебора значений [math]\alpha[/math] (или весь диапазон, в случае последовательной реализации)
- Остальные значения перебираются в заданном диапазоне -- обход дерева всех наборов значений параметра (при заданном шаге по значениям).
1.3.1 Выбор диапазонов перебора для параметров каждой области
Вычисление диапазона перебора из настроек перебора (заданных при компиляции) и "порядкового номера" процесса (ранга в MPI_COMM_WORLD) можно отнести к вычислительному ядру
struct Area
{
double angle;
double kappa;
};
template<typename T>
struct Range
{
T min;
T max;
T step;
};
vector<Range<Area>> ParallelParams(int mpi_rank, int mpi_size)
{
vector<Range<Area>> ranges(AREAS_CNT);
constexpr double angle_step = (ANGLE_TO - ANGLE_FROM) / (double) RANGE_STEPS_CNT;
constexpr double kappa_step = (KAPPA_TO - KAPPA_FROM) / (double) RANGE_STEPS_CNT;
Range<Area> r0 = { { ANGLE_FROM + mpi_rank * angle_step, 1 }, { ANGLE_FROM + (mpi_rank + 1) * angle_step, 1 },{ angle_step, kappa_step } };
Range<Area> r1 = { { ANGLE_FROM, KAPPA_FROM },{ ANGLE_TO, KAPPA_TO },{ angle_step, kappa_step } };
ranges[0] = r0;
for (size_t i = 1; i < AREAS_CNT; ++i)
ranges[i] = r1;
return ranges;
}
1.3.2 Перебор на заданных диапазонах
Проверяется выполнения правого граничного условия при заданных условиях сопряжения решения в областях (условия зависят от параметров [math]\varkappa, \alpha[/math]) и заданном левом граничном условии.
Способ обхода выбран таким образом, чтобы переход к следующему набору параметров требовал наименьшее число операций, для этого же используется стек T из n = AREAS_CNT матриц 2x2.
struct Matrix
{
double elems[2][2];
};
const Matrix IdentityMatrix = { { { 1, 0 }, { 0, 1 } } };
inline void RotateScale(Matrix& out, const Matrix& in, double phi, double scale = 1.0)
{
double c = cos(phi);
double s = sin(phi);
out.elems[0][0] = in.elems[0][0] * c + in.elems[1][0] * s;
out.elems[0][1] = in.elems[0][1] * c + in.elems[1][1] * s;
out.elems[1][0] = scale * (- in.elems[0][0] * s + in.elems[1][0] * c);
out.elems[1][1] = scale * (- in.elems[0][1] * s + in.elems[1][1] * c);
}
int vector<vector<Area>> CheckRBoundaryCond(vector<Range<Area>> ranges)
{
vector<vector<Area>> results;
vector<Area> areas(AREAS_CNT);
vector<Matrix> T(AREAS_CNT);
for (size_t i = 0; i < AREAS_CNT; ++i)
areas[i] = ranges[i].min;
T[0] = IdentityMatrix;
for (size_t i = 1; i < AREAS_CNT; ++i)
RotateScale(T[i], T[i - 1], areas[i - 1].angle, areas[i - 1].kappa / areas[i].kappa);
for (int lvl = AREAS_CNT; lvl > 0; ) {
// check boundary condition if at top lvl area
if (lvl == AREAS_CNT) {
double angle = 0.0;
for (size_t i = 0; i < AREAS_CNT; ++i)
angle += areas[i].angle;
double rbcond = T.back().elems[0][1] * cos(angle) + T.back().elems[1][1] * sin(angle);
if (abs(rbcond) < EPS) {
results.push_back(areas);
}
lvl--;
continue;
}
// try increase kappa at lvl-th area and go up
double next_kappa = areas[lvl].kappa + ranges[lvl].step.kappa;
if (next_kappa <= ranges[lvl].max.kappa + 0.5 * ranges[lvl].step.kappa) {
areas[lvl].kappa = next_kappa;
RotateScale(T[lvl], T[lvl - 1], areas[lvl - 1].angle, areas[lvl - 1].kappa / areas[lvl].kappa);
lvl++;
continue;
}
// try increase angle at lvl-th area and go up
double next_angle = areas[lvl].angle + ranges[lvl].step.angle;
if (next_angle <= ranges[lvl].max.angle + 0.5 * ranges[lvl].step.angle) {
areas[lvl].angle = next_angle;
RotateScale(T[lvl], T[lvl - 1], areas[lvl - 1].angle, areas[lvl - 1].kappa / areas[lvl].kappa);
lvl++;
continue;
}
// jump to previous area
areas[lvl] = ranges[lvl].min;
lvl--;
}
return results;
}
1.4 Макроструктура алгоритма
- Для каждого процесса из его номера вычисляется поддерево наборов значений для обхода.
- Каждым из процессов выполняется обход своего поддерева
- 0-ой процесс, закончив обход своего поддерева, собирает все результаты и сохраняет их в файл с уникальным именем
1.5 Схема реализации последовательного алгоритма
Приведенная выше паралелльная реализация является эффективной последовательной:
CheckRBoundaryCond(ParallelParams(0, 1)) // 0 - номер процесса, 1 - количество процессов
Подробнее см. раздел вычислительное ядро
1.6 Последовательная сложность алгоритма
- n - число областей непрерывности [math]\varkappa[/math]
- k - число пробных значений в диапазоне перебора
сложноcть последовательной реализации -- [math]O(k^{2n})[/math]
1.7 Информационный граф
mpi_rank, mpi_size = p -- ранг процесса в MPI_COMM_WORLD, размер MPI_COMM_WORLD (число процессов)
n -- число областей непрерывности
1.8 Ресурс параллелизма алгоритма
Пусть [math]p[/math] -- число параллельных процессов, тогда паралелльная сложность -- амортизированное [math]O(k^{2n - p})[/math] (в сравнении с последовательной [math]O(k^{2n})[/math]), так как пересылка и сохранение результатов в конце занимают намного меньше времени чем сам перебор, который распараллеливается с линейной масштабируемостью.
1.9 Входные и выходные данные алгоритма
Параметрами задачи являются: число областей непрерывности, диапазон и точность перебора [math]\varkappa, \alpha[/math], требуемая точность выполнения граничного условия. Они определены в коде как константы (задаются во время компиляции)
В данной реализации "входными данными" времени исполнения является лишь идентификатор процесса и количество процессов.
В качестве выходных данных было взято число всех найденных наборов [math]\{ \varkappa\}, \{ \alpha\}[/math], удовлетворяющих требованиям с заданной точностью.
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
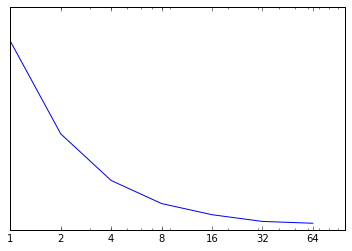
Масштабируемость линейная. Ключевым ограничением масштабируемости может стать только сбор и сохранение всех результатов одним процессом, но он занимает очень мало времени по сравнению с перебором.
Ось абсцисс -- число процессов (логарифмическая шкала), ось ординат -- время (линейная шкала). Получилось что-то похожее на [math]t = 1/p[/math]
Пример: JobId = 1382989, p = 128, Time = 00:14
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
- Алгоритм имеет линейную масштабируемость на любой системе, где сохранение данных не займет существенную часть времени. (вычислительные ядра не взаимодействуют)
- Алгоритм не учитывает возможность оптимизации с помощью векторизации.
2.7 Существующие реализации алгоритма
Задача очень специфическая, поэтому других существующих реализаций не найдено.
3 Литература
Диссертация: Дудкина А.А. "К [math]L_p[/math]-теории эллиптических краевых задач с разрывными коэффицентами", Москва, 2009