Участник:Artem.sevastopolsky/Преобразование Хаффа

Преобразование Хаффа для поиска наиболее выраженных прямых линий на изображении
Последовательный алгоритм
Последовательная сложность	[math]O(NMK_\theta)[/math]
Объём входных данных	[math]O(NM)[/math]
Объём выходных данных	[math]O(K_\theta \sqrt{N^2 + M^2})[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(1)[/math] (с учетом блокировок чтения/записи памяти — [math]O(K_\theta + NM)[/math])
Ширина ярусно-параллельной формы	[math]O(NMK_\theta)[/math]

Автор статьи: Севастопольский Артем

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Преобразование Хаффа — это преобразование бинарного изображения, которое позволяет эффективно найти его наиболее выраженные прямые линии. Метод переводит бинарное изображение в изображение в специальном пространстве (пространстве Хаффа), в котором каждая ячейка отвечает за определённую линию. Преобразование было предложено П. Хаффом (P. Hough) в 1962 г. с целью создания метода для регистрации следов быстрых заряженных ионизирующих частиц в пузырьковой камере, и, потенциально, для поиска произвольных сложных шаблонов на фотографии. В своём патенте П. Хафф предлагает электронную схему, реализация которой способна регистрировать следы пролетающих частиц, в то время как сам алгоритм в его современном описании был описан А. Розенфельдом (A. Rozenfeld) и другими математиками. Метод является одним из популярных и цитируемых методов в компьютерной графике.

Преобразование Хаффа используется в компьютерном зрении и цифровой обработке изображений для извлечения признаков из изображения. Алгоритм позволяет найти прямые линии, даже если они разрывны, пересекаются с другими линиями, являются частями более сложных линий, или если прямой принадлежат точки из разных частей изображения. В силу низкой вычислительной сложности ([math]O(NMK)[/math], где [math]N, M[/math] — размеры изображения, [math]K[/math] — число уровней квантования наклона прямой), алгоритм является одним из эффективных методов поиска прямых линий, и более эффективен, чем перебор по всевозможным линиям. Преобразование применяется к бинарному изображению, но его можно адаптировать для анализа произвольного черно-белого или цветного изображения, например, фотографии. Для этого необходимо применить к изображению любой детектор контуров, например, детектор Canny , и далее работать с получившимся бинарным изображением.

За количество линий, которые считаются наиболее выраженными, отвечает значение специального порога, которое необходимо задать пользователю. Необходимость ручного подбора количества наиболее выраженных линий может считаться недостатком метода.

Метод имеет много модификаций, предназначенных для его ускорения или изменения его свойств. Одними из самых популярных модификаций алгоритма являются его варианты для поиска окружностей и эллипсов. Эти модификации обладают аналогичными свойствами и позволяют находить окружности и эллипсы, даже если на изображении они разрывны. Кроме того, возможен поиск более сложных аналитических кривых и кривых без параметризации (Generalized Hough Transform).

Вычислительное ядро алгоритма поиска прямых линий представляет собой один тройной вложенный цикл, из тела которого производятся обращения записи в общую память, поэтому метод успешно подвергается распараллеливанию. При поиске кривой, параметризуемой [math]m[/math] параметрами ([math]m=2[/math] для прямой линии, [math]m=3[/math] — для окружности, и т.д.), временная сложность повышается до [math]O(NMK^{m-1})[/math] (при условии, что число уровней квантования всех параметров, кроме одного, равно [math]K[/math]). Это представляет основную проблему применения метода на практике для сложных линий. Однако, т. к. вид алгоритма не меняется относительно алгоритма поиска прямых линий, модифицированный метод также допускает распараллеливание.

1.2 Математическое описание алгоритма

Пусть имеется бинарное изображение [math]I(i, j), i \in \overline{0, N - 1}, j \in \overline{0, M - 1}[/math] (интенсивность каждого пикселя равна либо нулю, либо единице). Преобразование Хаффа заключается в построении специального изображения — аккумулятора — по исходному изображению. Пространство, которому принадлежит аккумулятор, называют пространством Хаффа. Обозначим аккумулятор через [math]A(\rho, \theta), \rho \in \overline{0, K_{\rho} - 1}, j \in \overline{0, K_{\theta} - 1}[/math]. [math]K_{\rho}[/math] выбирают равным [math]\lceil 2 \cdot \sqrt{N^2 + M^2} \rceil[/math] для простоты реализации и наибольшей точности (тем не менее, можно переписать алгоритм так, чтобы [math]K_{\rho}[/math] было произвольным, возможно, не зависящим от [math]N, M[/math]). [math]K_{\theta}[/math] выбирают произвольной константой, но наиболее естественным является выбор [math]K_{\theta} = 180[/math] (по одному уровню квантования на каждый градус угла).

Каждый элемент аккумулятора отвечает определённой прямой линии: элемент [math]A(\rho + \sqrt{N^2 + M^2}, \theta)[/math] соответствует прямой, имеющей уравнение [math]x\cos\theta + y\sin\theta = \rho.[/math] В таком уравнении прямой [math]\rho[/math] имеет смысл длины перпендикуляра (со знаком) к прямой от начала координат, [math]\theta[/math] — угла между перпендикуляром и горизонтальной осью. Любая линия, проходящая через точки изображения, имеет единственную такую параметризацию.

Алгоритм преобразования изображения в пространство Хаффа имеет следующий вид:

   А[i][j] := 0 для всех i, j;
   для каждого t от 0 до [math]K_{\theta}[/math] - 1
       [math]\theta_t = -\frac{\pi}{2} + \frac{\pi \cdot t}{K_\rho}[/math]
       для каждого i от 0 до [math]N[/math] - 1
           для каждого j от 0 до [math]M[/math] - 1
               если I[i][j] не равно 0,
                   [math]\rho_t := round(j \cdot \cos\theta_t + i \cdot \sin\theta_t + \sqrt{N^2 + M^2})[/math], где [math]round(x)[/math] — функция округления числа [math]x[/math] до ближайшего целого
                   A[[math]\rho_t[/math]][t] += 1

Таким образом, для каждой белой точки изображения I в аккумуляторе инкрементируется ячейка каждой прямой, которая проходит через данную точку. Во внешнем цикле происходит перебор по углам наклона линии.

После проведения указанных действий в массиве А содержится аккумулятор для изображения I. Для того чтобы получить наиболее выраженные прямые по данным из аккумулятора, необходимо взять [math]T[/math] максимальных значений элементов аккумулятора и сопоставить им их прямые линии. Параметр метода [math]T[/math] необходимо либо подобрать вручную, либо выбрать на основе значений аккумулятора.

Стоит заметить, что если число белых пикселей изображения I мало по сравнению с общим числомо пикселей, то имеет смысл заранее подсчитать позиции белых пикселей в отдельный массив, и затем запустить итерации по нему вместо двойного цикла по (i, j). Такая ситуация имеет место, к примеру, при работе с фотографиями после применения детектора контуров.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма составляет тройной вложенный цикл по переменным (t, i, j), описанный выше. Временная асимптотика выполнения цикла составляет [math]O(NMK_\theta)[/math], что на порядок больше, чем для остальных операций: загрузка изображения, инициализация аккумулятора, запись аккумулятора в файл требуют в сумме [math]O(NM + K_\theta \sqrt{N^2 + M^2})[/math] операций.

1.4 Макроструктура алгоритма

Алгоритм не использует другие алгоритмы в качестве составных частей.

1.5 Схема реализации последовательного алгоритма

Схема реализации алгоритма повторяет схему, описанную в разделе #Математическое описание алгоритма.

1.6 Последовательная сложность алгоритма

Разделим действия алгоритма на группы последовательных операций и оценим их временную сложность. Учитываются операции обновления значений переменных, считывания значений переменных, сложения, умножения, деления.

1. Загрузка изображения в оперативную память — [math]O(NM)[/math]

2. Инициализация аккумулятора — [math]O(K_\theta \sqrt{N^2 + M^2})[/math]

3. Основной тройной вложенный цикл (вычислительное ядро алгоритма) — [math]O(NMK_\theta)[/math]

4. Запись аккумулятора в файл — [math]O(K_\theta \sqrt{N^2 + M^2})[/math].

Итоговая сложность последовательного алгоритма — [math]O(NMK_\theta)[/math].

Если необходимо выделить сами линии, то дополнительный шаг (получение T максимумов в массиве аккумулятора за счет сортировки массива и построение T линий) требует [math]O(K_\theta \sqrt{N^2 + M^2} \log(K_\theta \sqrt{N^2 + M^2}) + T\sqrt{N^2 + M^2})[/math] операций.

1.7 Информационный граф

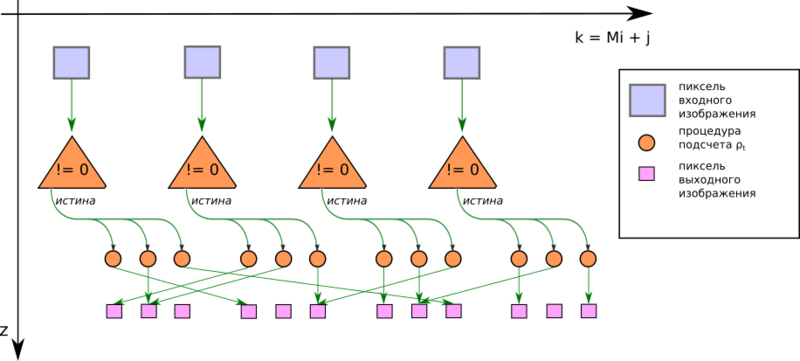
На Рис. 1 показан информационный граф алгоритма с расшифровкой условных обозначений операций. Т. к. все пиксели изображения обрабатываются одинаково, входные и выходные данные алгоритма расположены на рисунке так, как расположены пиксели изображений при их вытягивании в длинный вектор. Это также сделано для упрощения иллюстрации.

Рис. 1. Информационный граф алгоритма преобразования Хаффа.

Стрелки из операций вычисления [math]\rho_t[/math] в пиксели выходного изображения обозначают операцию инкремента (прибавления единицы в соответствующую ячейку аккумулятора). Параметр [math]\rho_t[/math] и уровень квантования угла [math]t[/math] влияет на выбор конкретной ячейки аккумулятора. Из каждого желтого круга выходит ровно одна стрелка в фиолетовый квадрат. В каждый фиолетовый квадрат может входить как 0, так и 1 или более стрелок.

1.8 Ресурс параллелизма алгоритма

Для оценки ресурса параллелизма алгоритма будем рассматривать его вычислительное ядро. Заметим, что цикл подвергается распараллеливанию при условии, если выполнены следующие модификации:

• значение пикселя I[i][j] считывается из памяти атомарно,
• значение пикселя A[[math]\rho_t[/math]][t] инкрементируется атомарно,
• вычисление значения [math]\rho_t[/math] производится внутри самого внутреннего цикла.

Заметим, что высота ярусно-параллельной формы алгоритма является постоянной, т.е. параллельная сложность алгоритма составляет О(1) в терминах следующих операций: проверка условия (условный оператор), умножения, сложения, округления. Однако заметим, что параллельный алгоритм расчитан на обращение к изображению и аккумулятору, находящихся в общей памяти. Считывания памяти и записи в память необходимо производить атомарно, поэтому в терминах указанных операций и операций атомарного считывания/записи общей памяти параллельная сложность алгоритма составляет [math]O(K_\theta + NM)[/math] (максимальное число одновременных обращений в общую память). Тем не менее, при числе потоков, много меньшем общего числа итераций циклов, и при случайном распределении задач по потокам можно считать, что на практике алгоритм имеет параллельную сложность О(1).

Для ускорения работы целесообразно подсчитать значения [math]\cos(\theta_t)[/math] и [math]\sin(\theta_t)[/math] для всех [math]t[/math] заранее и сохранить в соответствующие массивы. В этом случае надо либо расположить массивы в общей памяти и производить атомарные чтения из них, либо скопировать эти массивы в память каждого потока. Было исследовано, что последний вариант работает быстрее.

1.9 Входные и выходные данные алгоритма

• Входные данные алгоритма: бинарное изображение [math]I(i, j), i \in \overline{0, N - 1}, j \in \overline{0, M - 1}[/math].
• Выходные данные алгоритма: аккумулятор [math]A(\rho, \theta), \rho \in \overline{0, \lceil 2 \cdot \sqrt{N^2 + M^2} \rceil - 1}, j \in \overline{0, K_{\theta} - 1}[/math], тип значения в ячейке — целочисленный.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

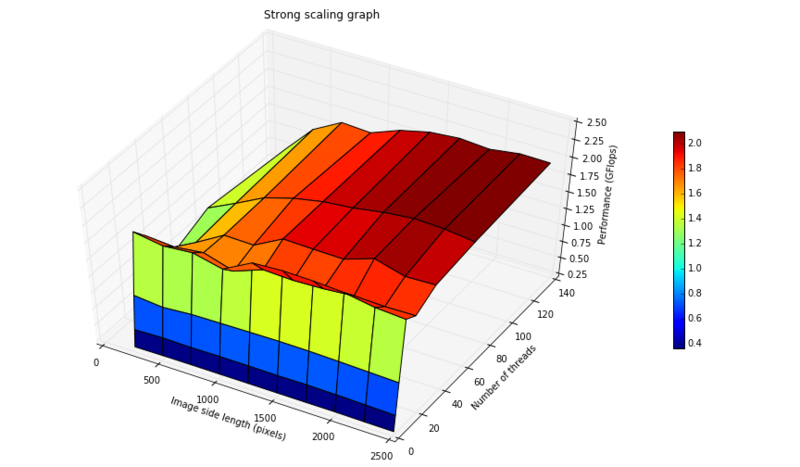
На Рис. 2 показан график сильной масштабируемости для рассматриваемого алгоритма. Отображена зависимость числа операций над вещественными числами в секунду от размера входного изображения и числа потоков. В качестве входного изображения было взято полностью белое изображение с целью рассмотреть худший случай работы алгоритма. Заметим, что число вещественных операций зависит от числа белых пикселей на изображении и не зависит от размера изображения.

Рис. 2. График сильной масштабируемости

График сильной масштабируемости показывает, что чем больше используется потоков, тем выше производительность (и ниже время работы) алгоритма (за исключением случая, когда изображение малого размера). Тем не менее, стоит заметить, что при числе потоков большем, чем 8 или 16, рост производительности происходит медленнее, чем при числе потоков от 1 до 8 (но всё же линейно). Причина, по которой может наблюдаться такой эффект, — это необходимые блокировки для считывания и записи данных, находящихся в общей памяти. Как уже было отмечено в разделе #Ресурс параллелизма алгоритма, эти операции увеличивают параллельную сложность, но данный эффект заметен только при достаточно большом числе потоков.

Т. к. прирост производительности при числе потоков, много большем 16, по сравнению с числом потоков, равным 16, невелик, представляется разумным выбор числа потоков равным 16 или 32.

2.7 Существующие реализации алгоритма

Известные последовательные реализации алгоритма:

• OpenCV реализует классическое и вероятностное преобразование Хаффа для прямых линий и окружностей. Библиотека имеет интерфейсы для C++ и Python.
• Scikit-image реализует классическое и вероятностное преобразование Хаффа для прямых линий, окружностей и эллипсов, а также функцию для выбора сильно отличающихся прямых по данным аккумулятора преобразования (skimage.transform.hough_line_peaks). Библиотека имеет интерфейс только для Python.
• Встроенная реализация в Matlab для поиска прямых линий. Также имеется реализация для поиска окружностей.