Участник:Avasilenko/Partitioning Around Medoids (PAM)

Эта работа успешно выполнена Преподавателю: в основное пространство, в подстраницу Данное задание было проверено и зачтено. Проверено Dexter и Zhum.

Partitioning Around Medoids
Последовательный алгоритм
Последовательная сложность	[math]O(T*kn^2)[/math]
Объём входных данных	[math]n*(n-1)+2[/math]
Объём выходных данных	[math]k+1[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(T*kn)[/math]
Ширина ярусно-параллельной формы	[math]O(k(n-k))[/math]

Авторы:

• А.Э.Василенко (отвечает за программистскую составляющую);
• А.В.Тузикова (отвечает за математическую составляющую).

Вклад авторов считать равноценным, чётких границ ответственности провести невозможно.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Объединение схожих объектов в группы - один из важнейших видов человеческой деятельности. Более того - это важная часть процесса познания мира, в котором мы живем. Мы учим детей различать кошек и собак, воду и песок, мужчин и женщин путем постоянного развития и улучшения подсознательных схем классификации. Примеры есть и во взрослой жизни – в химии необходимо классифицировать соединения, в археологии – объединять находки по периодам и т.д.

Задача кластеризации - разделение множества объектов на заданное число множеств с минимизацией некоторого функционала - является популярной задачей, относится к разделу машинного обучения и находит применение в таких областях, как анализ текста, биоинформатика, интеллектуальные транспортные системы и др.

Существует несколько видов кластеризации:

• плоская кластеризация (flat clustering) - порождает совокупность кластеров, не имеющих явных взаимосвязей;
• иерархическая кластеризация (hierarchical clustering) - создаёт иерархию кластеров.

PAM (Partitioning Around Medoids) - плоский алгоритм кластеризации, позволяющий выделить [math]k[/math] кластеров (множеств), удовлетворяющих следующим свойствам:

• каждая группа содержит хотя бы один объект;
• каждый объект принадлежит ровно одной группе.

Модель , лежащая в основе алгоритма PAM, основана на выборе [math]k[/math] объектов, являющихся характерными точками соответствующего кластера. Таким образом, кластерам сопоставляются принадлежащие им объекты, называемые медоидами, на основании которых распределяются остальные объекты по принципу наибольшего сходства. Cама модель называется моделью k-medoids (не путать с моделью k-median).

PAM состоит из двух фаз: BUILD и SWAP:

• на фазе BUILD выполняется первичная кластеризация, в ходе которой последовательно выбираются [math]k[/math] объектов в качестве медоидов;
• фаза SWAP представляет собой итерационный процесс, в ходе которого производятся попытки улучшить множество медоидов. Алгоритм выполняет поиск пары объектов (медоид, не-медоид), минимизирующих целевую функцию при замене, после чего обновляет множество медоидов.

На каждой итерации алгоритма выбирается пара (медоид, не-медоид) такая, что замена медоида [math]x_{m_l}[/math] на не-медоид [math]x_{o_h}[/math] дает лучшую кластеризацию из возможных. Оценка кластеризации выполняется с помощью целевой функции, вычисляемой как сумма расстояний от каждого объекта до ближайшего медоида:

[math]E = \sum_{j = 1}^n \min_{1 \leq l \leq k} \rho ( x_{m_l},x_{o_j} )[/math]

Процедура изменения множества медоидов повторяется, пока есть возможность улучшения значения целевой функции.

1.2 Математическое описание алгоритма

Исходные данные:

• множество кластеризуемых объектов [math]X = \{ x_1, x_2, ... , x_n \} [/math], где [math]x_i[/math] - кортеж, состоящий из [math] w [/math] вещественных чисел;
• симметрическая матрица [math]D[/math], элементы матрицы [math]d_{ij}=d(i,j)[/math] - вычисленные расстояния между объектами [math]x_i, x_j[/math];
• количество кластеров [math]k \leq n.[/math]

Обозначения:

• [math]M = \{ x_{m_1}, x_{m_2}, ... , x_{m_k} \} [/math] - множество медоидов, [math] M \subseteq X ;[/math]
• [math]O = \{ x_{o_1}, x_{o_2}, ... , x_{o_r} \} [/math] - множество не-медоидов, [math] O \subseteq X, [/math] где [math]r=n-k;[/math]
• [math]d_{ij}=\rho (x_i, x_j )[/math], где [math] \rho : X \times X \rightarrow R [/math] — метрика расстояния;
• [math]F_{M,O} = \sum_{j = 1}^{n} \min_{ x_{m_l} \in M} \rho ( x_{m_l},x_{o_j} )[/math] - значение целевой функции для заданных множеств [math]M[/math] и [math]O;[/math]
• [math]T^i[/math] - изменение целевой функции на [math]i[/math]-м шаге фазы SWAP.

Выходные данные:

• [math]M = \{ x_{m_1}, x_{m_2}, ... , x_{m_k} \}[/math] - множество медоидов;
• [math]K_{m_i} = \{ x_{o_h} \in O \| x_{m_i} = \arg \min_{x_{m_s} \in M} \rho (x_{o_h}, x_{m_s}) \}, 1 \leq i \leq k[/math] - искомые кластеры.

Вычислительные формулы метода:

• фаза BUILD (состоит из [math]k[/math] шагов последовательного выбора [math]k[/math] медоидов):
  • [math]O_0 = X, M_0 = \varnothing ;[/math]
  • [math]x_{m_1} = \arg \min_{x_{o_h} \in O_0} \sum_{j = 1}^n \rho \left ( x_{o_h},x_j \right ), O_1 = O_0 \backslash \{x_{m_1}\}, M_1 = M_1 \cup \{x_{m_1}\} ; [/math]
  • [math]x_{m_2} = \arg \min_{x_{o_h} \in O_1} \sum_{j = 1}^{n} \min ( \rho ( x_{m_1},x_j ), \rho ( x_{o_h},x_j ) ), O_2 = O_1 \backslash \{x_{m_2}\}, M_2 = M_1 \cup \{x_{m_2}\} ; [/math]
  • [math]x_{m_3} = \arg \min_{x_{o_h} \in O_2} \sum_{j = 1}^{n} \min_{1 \leq l \leq 2} ( \rho ( x_{m_l},x_j ) , \rho ( x_{o_h},x_j ) ) , O_3 = O_2 \backslash \{x_{m_3}\}, M_3 = M_3 \cup \{x_{m_3}\} ; [/math]
  • ...
  • [math]x_{m_k} = \arg \min_{x_{o_h} \in O_{k-1}} \sum_{j = 1}^{n} \min_{ x_{m_l} \in M_{k-1}} ( \rho ( x_{m_l},x_j ), \rho ( x_{o_h},x_j ) ) , O_k = O_{k-1} \backslash \{x_{m_k}\}, M_k = M_{k-1} \cup \{x_{m_k}\} ; [/math]

• фаза SWAP (итерационный процесс):
  • начальное приближение: [math]O_0 = O_k^{BUILD}, M_0 = M_k^{BUILD};[/math]
  • [math]i[/math]-й шаг итерации:
    • вычисление целевой функции при оптимальной замене (замене, при которой достигается лучшая кластеризация из возможных на текущей итерации):
      [math]F^i = \min_{x_{m_s} \in M_{i-1} , x_{o_h} \in O_{i-1}} \sum_{j = 1}^{n} \min_{ x_{m_l} \in M_{i-1} \backslash \{x_{m_s}\} } ( \rho ( x_{m_l},x_j ), \rho ( x_{o_h},x_j) ); [/math]
    • определение пары (медоид, не-медоид), на которой достигается оптимальная замена:
      [math] (x_{m_s}, x_{o_h}) = \arg F^i; [/math]
    • проверка критерия останова;
    • изменение множеств в соответствии с выбранной парой [math] (x_{m_s}, x_{o_h}):[/math]
      [math]M_i = M_{i-1} \backslash \{x_{m_s}\} \cup \{x_{o_h}\} , O_i = O_{i-1} \cup \{x_{m_s}\} \backslash \{x_{o_h}\} ;[/math]
  • критерий останова:
    • [math]T^i = F^{i-1} - F^{i} \leq 0 .[/math]

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма PAM на этапе BUILD состоит из многочисленных вычислений значений целевой функции при различных вариантах выбора дополнительного медоида (шаг алгоритма [math]1 \leq i \leq k[/math]):

[math]F^i = \min_{x_{o_h} \in O_{i-1}} \sum_{j = 1}^{n} \min_{ x_{m_l} \in M_{i-1}} ( \rho ( x_{m_l},x_j ), \rho ( x_{o_h},x_j ) ) = \min_{x_{o_h} \in O_{i-1}} \sum_{j = 1}^{n} \overline{MIN}_{i, x_{o_h}}^{(j)},[/math]

где:

• [math]\overline{MIN}_{1, x_{o_h} \in O_0} = \{ \rho (x_{o_h}, x_j ) \| 1 \leq j \leq n \};[/math]
• [math]\overline{MIN}_{i, x_{o_h} \in O_{i-1}} = \{ \min ( \overline{MIN}_{i-1, x_{m_{i-1}}}^{(j)}, \rho (x_{o_h}, x_j) ) \| 1 \leq j \leq n \}, \forall i: 1 \lt i \leq k.[/math]

С каждой итерацией количество вариантов выбора дополнительных медоидов уменьшается на единицу, таким образом, на [math]i[/math]-м шаге целевую функцию нужно вычислить лишь [math]|O_{i-1}| = n-i+1[/math] раз.

Оптимизация:

• таким образом, на каждой последующей итерации можно использовать величину, вычисленную на предыдущем шаге, что позволяет сократить число вычислений минимумов.

Вычислительное ядро алгоритма PAM на этапе SWAP состоит из многочисленных вычислений значений целевой функции при различных вариантах замены некоторого существующего медоида на элемент из числа не-медоидов. [math]i[/math]-я итерация фазы SWAP:

[math]F^i = \min_{x_{m_s} \in M_{i-1} , x_{o_h} \in O_{i-1}} \sum_{j = 1}^{n} \min_{ x_{m_l} \in M_{i-1} \backslash \{x_{m_s}\} } ( \rho ( x_{m_l},x_j ), \rho ( x_{o_h},x_j) ) =[/math]
[math]= \min_{x_{m_s} \in M_{i-1} } \min_{x_{o_h} \in O_{i-1}} \sum_{j = 1}^{n} \min ( \min_{ x_{m_l} \in M_{i-1} \backslash \{x_{m_s}\} } ( \rho ( x_{m_l},x_j )) , \rho ( x_{o_h},x_j) )[/math]

Оптимизация:

• таким образом, при поиске пары (медоид, не-медоид), наилучшим образом минимизирующей целевую функцию, происходит поиск минимума по всем возможным элементам [math]x_{o_h}[/math], для которых вычисляется [math]\sum_{j = 1}^{n} \min (a, b)[/math], где [math]a[/math] есть [math] \min_{ x_{m_l} \in M_{i-1} \backslash \{x_{m_s}\} } ( \rho ( x_{m_l},x_j )),[/math] и является инвариантом по отношению к [math]\min_{x_{o_h} \in O_{i-1}} \sum_{j = 1}^{n} \min ( \min_{ x_{m_l} \in M_{i-1} \backslash \{x_{m_s}\} } ( \rho ( x_{m_l},x_j )) , \rho ( x_{o_h},x_j) ),[/math] что позволяет предвычислить элемент [math]a.[/math]

1.4 Макроструктура алгоритма

Опишем макрооперации алгоритма:

• в случае если алгоритму PAM на вход подаётся набор точек с их координатами в пространстве [math]R^w,[/math] то необходимо вычислить матрицу расстояний. Для этого может быть использована, например, евклидова метрика:

  [math]\rho (p,q)=\sqrt{(p_1-q_1)^2+(p_2-q_2)^2+\dots+(p_w-q_w)^2} = \sqrt{\sum_{j=1}^w (p_j-q_j)^2} [/math], где [math]p, q \in R^w;[/math]

• нахождение минимального среди значений, принимаемых некоторой функцией [math]value,[/math] определённой на дискретном множестве [math]Y=\{y_i\}, \, i = \overline{(1,r)}:[/math]

  [math]minimum_{y \in Y } (value (y)) = \min \Bigg(value(y_1), \min \bigg(value(y_2), \min \Big(\dots , \min(value(y_{r-1}), value(y_{r})) ... \Big) \bigg)\Bigg);[/math]

• вычисление вектора инвариантов, используемых при оптимизации фазы SWAP (см. вычислительное ядро алгоритма):

  [math]\overline{a} = \{ minimum_{ x_{m_l} \in M_{i-1} \backslash \{x_{m_s}\} } ( \rho ( x_{m_l}, x_j ) ) \| 1 \leq j \leq n \},[/math] где [math]i - [/math]номер итерации;

• вычисление вектора расстояний от каждой точки заданного множества [math]X[/math] до ближайшего медоида из множества [math]M_{i-1} \backslash \{x_{m_s}\},[/math] где [math]i - [/math]номер итерации фазы SWAP:

  [math]\overline{b} = \{ \min (\overline{a}^{(j)}, \rho ( x_{o_p}, x_j )) \| 1 \leq j \leq n \};[/math]

• сложение компонент вектора: [math]S = \sum_{j = 1}^{n} \overline{f}^{(j)}.[/math]

Макроструктура вычислительного ядра алгоритма PAM может быть выражена через макрооперации следующим образом:

• для ядра фазы BUILD:

  [math]F^i = minimum_{ x_{o_h} \in O_{i-1} } ( S \, ( \overline{f} (x_{o_h}) )),[/math]

  [math]\overline{f} = \{ \min \,( \overline{MIN}_{i, x_{o_h}}^{(j)}, \rho (x_{o_h}, x_j)) \| 1 \leq j \leq n \}, [/math] где

  1. [math]S[/math] вычисляется [math]n-i+1[/math] раз;
  2. [math]minimum[/math] находится [math]1[/math] раз при вычислении наилучшего значения целевой функции на текущей итерации.

• для ядра фазы SWAP:

  [math]F^i = minimum_{ x_{m_s} \in M_{i-1} , x_{o_h} \in O_{i-1} } ( S \, ( \overline{b} \, ( x_{o_h}, \overline{a} \, (x_{m_s}) ) )),[/math] где:

  1. [math]minimum[/math] находится [math]n[/math] раз в процессе вычисления макрооперации [math]\overline {a};[/math]
  2. [math]\overline {a}[/math] вычисляется [math]k[/math] раз и использует вычисленные на шаге 1 минимальные значения;
  3. [math]\overline {b}[/math] вычисляется [math]k(n-k)[/math] раз и использует вычисленные на шаге 2 значения [math]\overline {a};[/math]
  4. [math]S[/math] вычисляется [math]k(n-k)[/math] раз и использует вычисленные на шаге 3 значения [math]\overline {b};[/math]
  5. [math]minimum[/math] находится [math]1[/math] раз при вычислении наилучшего значения целевой функции на текущей итерации.

1.5 Схема реализации последовательного алгоритма

Псевдокод алгоритма:

Вход  : Множество объектов [math]X[/math] или матрица расстояний [math]D[/math], количество кластеров [math]k[/math]
Выход : Множество медоидов [math]M[/math]
0  Если на вход было подано множество объектов, необходимо предварительно вычислить матрицу расстояний;
1  Инициализация множеств [math]M := \varnothing, O := X;[/math]
 
   // фаза BUILD
2  for (int i := 1; i <= k; i++) {
       // Найти [math]x_{m_i}:[/math]
       {
3          Для всех [math]x_{o_h} \in O[/math] вычислить [math]F_{M \cup \{x_{o_h}\}, O \backslash \{x_{o_h}\}};[/math]
4          Положить [math]x_{m_i}[/math] равным [math]x_{o_h}[/math], соответствующему минимальному из вычисленных [math]F;[/math]
       }
5      Обновить множества [math]M := M \cup \{x_{m_i}\}, O := O \backslash \{x_{m_i}\};[/math]
   }
   // фаза SWAP
6  while (1) {
       // Найти пару [math](x_{m_s}, x_{o_h}),[/math] на которой достигается оптимальная замена:
       {
7          Для всех [math]x_{m_i} \in M, x_{o_j} \in O[/math] вычислить [math]F^i;[/math] // вычисление проводить с учётом приведённой ранее оптимизации (см. 1.3 Вычислительное ядро алгоритма);
8          Положить пару [math](x_{m_s}, x_{o_h})[/math] равной паре [math](x_{m_i}, x_{o_j})[/math], соответствующей минимальному из вычисленных [math]F;[/math]
       }
9      Вычислить [math]T^i;[/math] // критерий останова (см. 1.2 Математическое описание алгоритма)
10     if [math](T^i \gt  0)[/math] {
11         Обновить множества [math]M := M \backslash \{x_{m_s}\} \cup \{x_{o_h}\}, O := O \cup \{x_{m_s}\} \backslash \{x_{o_h}\};[/math]
12     } else {
13         break;
       }
   };

Оптимизации:

• Предвычисление матрицы расстояний. Необходимо предварительно вычислить матрицу расстояний и сохранить её в памяти, так как в ходе вычисления алгоритма многократно используются расстояния между элементами, а вычисление каждого из них является ресурсоёмкой операцией из нескольких умножений и одного извлечения квадратного корня.

• Минимизация кеш-промахов. Матрица расстояний, к которой постоянно выполняется доступ на чтение для вычисления минимумов и их суммирования, должна храниться в памяти как матрица размера [math]n*n[/math], несмотря на то, что она симметрическая и достаточно хранить лишь половину (элементы над или под главной диагональю). Данная оптимизация потребует использования в 2 раза большего количества памяти для хранения расстояний (а это является главным расходом памяти программы, так как все остальные используемые данные являются временными (локальными для каждой операции) и представляют из себя несколько векторов длинной [math]n[/math] элементов). Однако так как в данном алгоритме доступ к матрице осуществляется построчно (в вычислительном ядре алгоритма поэлементно ищутся минимумы 2-х векторов, после чего все они складываются), то в этом случае из матрицы можно будет читать данные по строкам подряд, что снижает количество кеш-промахов. Использование только половины матрицы приводит к частым промахам в кеше в связи с необходимостью загрузки части векторов по строкам, а части - по столбцам.

1.6 Последовательная сложность алгоритма

Для вычисления матрицы расстояний требуется:

• [math]\frac{n*(n-1)}{2}[/math] операций вычисления расстояний;
• сложность каждой операции вычисления расстояния (для случая использования Евклидовой метрики) равна [math]2*w-1[/math] операций сложения и вычитания, [math]w[/math] операций возведения в квадрат (умножения) и [math]1[/math] операции извлечения квадратного корня.

На основании формулы из описания вычислительного ядра фазы BUILD определим сложность выполнения всего этапа.

Обозначим:

• [math]summs[/math] - операция сложения двух вещественных чисел;
• [math]mins[/math] - операция нахождения минимума для двух вещественных чисел.

Тогда, количество операций равно:

[math]S = ( ( (n-1) summs ) * (n-1+1) + (n-1+1-1)mins) + \sum_{i = 2}^{k} ( ( (1 mins)*(n-1) + (n-1) summs ) * (n-i+1) + (n-i+1-1)mins) \Rightarrow[/math]
[math] \Rightarrow S = \begin{cases} S(mins) = ( ( 0 ) * (n-1+1) + (n-1+1-1)mins) + \sum_{i = 2}^{k} ( ( (1 mins)*(n-1)) * (n-i+1) + (n-i+1-1)mins ) & \quad\\ S(summs) = \sum_{i = 1}^{k} ( ( (n-1) summs ) * (n-i+1) ) & \quad\\ \end{cases} = [/math]

[math] = \begin{cases} S(mins) = n^2(k-1) - \frac{1}{2}(nk^2 - nk) + n - k & \quad\\ S(summs) = n^2k - \frac{1}{2}(nk^2 + nk - k^2 + k ) & \quad\\ \end{cases} [/math]

Таким образом, сложность фазы BUILD есть [math]O(kn^2)[/math] как по количеству найденных минимумов, так и по количеству операций сложения.

На основании формулы из описания вычислительного ядра фазы SWAP определим сложность вычисления целевой функции [math]F^i[/math] с использованием оптимизации процесса нахождения минимума (см. раздел Вычислительное ядро алгоритма). Количество операций равно:

[math]S = ( ( (1 mins)*(n-1) + (n-1) summs )*(n-k) + n*((k-1-1) mins) )*k \Rightarrow[/math]
[math] \Rightarrow S = \begin{cases} S(mins) = ( ((1 mins)*(n-1) )*(n-k) + n*((k-1-1) mins) )*k = kn^2 - 3nk + k^2 & \quad\\ S(summs) = ( ( (n-1) summs )*(n-k) )*k = (n-1)(n-k)k & \quad\\ \end{cases} [/math]

Таким образом, сложность одной итерации фазы SWAP есть [math]O(kn^2)[/math] как по количеству найденных минимумов, так и по количеству операция сложения.

Полученные оценки позволяют говорить о том, что PAM относится к алгоритмам с квадратичной сложностью.

Основная вычислительная сложность алгоритма PAM приходится на фазу SWAP, т.к. сложность одной её итерации сопоставима со сложностью всей фазы BUILD, однако SWAP может содержать в себе огромное число итераций.

1.7 Информационный граф

1.7.1 Информационный граф фазы BUILD

Опишем граф фазы BUILD как аналитически, так и в виде рисунка.

Граф состоит из шести групп вершин:

1. Операция M, соответствующая первой группе вершин, осуществляет изменение множества медоидов:

   [math]M_{It} = M_{It-1} \cup \overline{x}_{m_{It}}, [/math] где [math]\overline{x}_{m_{It}} = \overline{x}_{o_{It}}.[/math]

   Единственная координата [math]It[/math] (номер итерации), соответствующая каждой из вершин, меняется в диапазоне [math][1; k],[/math] принимая все целочисленные значения.

   Аргументами операции являются:

   • [math]\overline{x}_{o_{It}}[/math] - результат срабатывания операции, соответствующей вершине из пятой группы с координатой [math]It,[/math]
   • [math]M_{It-1}[/math] - множество медоидов:
     • при [math]It = 1 [/math] - входное данное алгоритма;
     • при [math]1\lt It \leq k [/math] - результат срабатывания операции, соответствующей вершине из первой группы с координатой [math]It-1.[/math]

   Результат срабатывания операции является:

   • при [math]It \lt k [/math] - промежуточным данным алгоритма;
   • при [math]It = k [/math] - выходным данным фазы BUILD.

   
   

2. Операция O, соответствующая второй группе вершин, осуществляет изменение множества не-медоидов:

   [math]O_{It} = O_{It-1} \backslash \overline{x}_{o_{It}}.[/math]

   Единственная координата [math]It[/math], соответствующая каждой из вершин, меняется в диапазоне [math][1; k],[/math] принимая все целочисленные значения.

   Аргументами операции являются:

   • [math]\overline{x}_{o_{It}}[/math] - результат срабатывания операции, соответствующей вершине из пятой группы с координатой [math]It,[/math]
   • [math]O_{It-1}[/math] - множество не-медоидов:
     • при [math]It = 1 [/math] - входное данное алгоритма;
     • при [math]1\lt It \leq k [/math] - результат срабатывания операции, соответствующей вершине из второй группы с координатой [math]It-1.[/math]

   Результат срабатывания операции является:

   • при [math]It \lt k [/math] - промежуточным данным алгоритма;
   • при [math]It = k [/math] - выходным данным фазы BUILD.

   
   

3. Операция, соответствующая третьей группе вершин, выглядит следующим образом:

   [math]\overline{c}=\overline{c}_{x_{o_p} } = \begin{cases} \{ \rho (x_{o_p}, x_j ) \| 1 \leq j \leq n \}, It=1 & \quad\\ \{ \min ( \overline{MIN}^{(j)}, \rho (x_{o_p}, x_j) ) \| 1 \leq j \leq n \}, 1\lt It \leq k & \quad\\ \end{cases} .[/math]

   Координаты вершин:

   • [math]It[/math] - меняется в диапазоне [math][1; k],[/math] принимая все целочисленные значения;
   • [math]p[/math] - меняется в диапазоне [math][1; n-It+1],[/math] принимая все целочисленные значения.

   Аргументами операции являются:

   • при [math]It = 1:[/math]
     • [math]\overline{x}_{o_p}[/math] - входное данное алгоритма;
   • при [math]1 \lt It \leq k:[/math]
     • [math]\overline{x}_{o_p}[/math] - результат срабатывания операции, соответствующей вершине из второй группы с координатой [math]It-1;[/math]
     • [math]\overline{MIN}[/math] - результат срабатывания операции, соответствующей вершине из шестой группы с координатой [math]It-1.[/math]

   Результат срабатывания операции является промежуточным данным алгоритма.

   
   

4. Операция S, соответствующая четвертой группе вершин, выглядит следующим образом:

   [math]S = \sum_{j = 1}^{n} \overline {c}^{(j)}.[/math]

   Координаты вершин:

   • [math]It[/math] - меняется в диапазоне [math][1; k],[/math] принимая все целочисленные значения;
   • [math]p[/math] - меняется в диапазоне [math][1; n-It+1],[/math] принимая все целочисленные значения.

   Аргументами операции являются:

   • [math]\overline{c}_{ x_{o_p} }[/math] - результат срабатывания операции, соответствующей вершине из третьей группы с координатами [math] It, p.[/math]

   Результат срабатывания операции является промежуточным данным алгоритма.

   
   

5. Операция M1, соответствующая пятой группе вершин, выглядит следующим образом:

   [math]M1 = (F^{It}; x_{o_{It}}),[/math] где [math] \begin{cases} F^{It} = \min_{x_{o_p} \in O_{It-1}} S & \quad\\ x_{o_{It}} = \arg F^{It} & \quad\\ \end{cases}[/math]

   Координаты вершин:

   • [math]It[/math] - меняется в диапазоне [math][1; k],[/math] принимая все целочисленные значения.

   Аргументами операции являются:

   • [math]S[/math] - результаты срабатывания операций, соответствующих вершинам из четвертой группы с первой координатой [math]It,[/math] всего [math]n-It+1[/math] величина.

   Результат срабатывания операции является:

   • при [math]It \lt k [/math] - промежуточным данным алгоритма;
   • при [math]It = k [/math] - выходным данным фазы BUILD.

   
   

6. Операция MIN, соответствующая шестой группе вершин, выглядит следующим образом:

   [math]\overline{MIN}=\overline{MIN}_{It,x_{m_{It}} } = \begin{cases} \{ \rho (x_{m_{It} }, x_j ) \| 1 \leq j \leq n \}, It=1 & \quad\\ \{ \min ( \overline{MIN}^{(j)}, \rho (x_{m_{It}}, x_j) ) \| 1 \leq j \leq n \}, 1\lt It \leq k & \quad\\ \end{cases}[/math]

   Координаты вершин:

   • [math]It[/math] - меняется в диапазоне [math][1; k-1],[/math] принимая все целочисленные значения.

   Аргументами операции являются:

   • [math]\overline{MIN}_{It-1,x_{m_{It-1}}} [/math] - результат срабатывания операции, соответствующей вершине из шестой группы с координатой [math]It-1;[/math]
   • [math]x_{m_{It}} = x_{o_{It}} [/math] - результат срабатывания операции, соответствующей вершине из пятой группы с координатой [math]It.[/math]

   Результат срабатывания операции является промежуточным данным алгоритма.

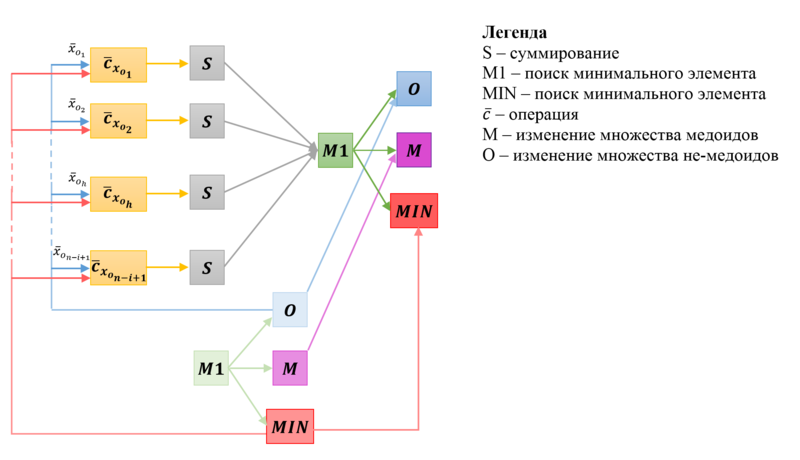
Описанный граф в общем случае представлен на Рис.1, отображен шаг с номером [math]It, 1\lt It\lt k[/math] фазы BUILD. Обозначения:

1. вершины первой группы обозначены фиолетовым цветом и подписаны как [math]M;[/math]
2. вершины второй группы обозначены синим цветом и подписаны как [math]O;[/math]
3. вершины третьей группы обозначены жёлтым цветом и подписаны как [math]\overline{c}_{x_{o_p} };[/math]
4. вершины четвертой группы обозначены серым цветом и подписаны как [math]S;[/math]
5. вершины пятой группы обозначены зеленым цветом и подписаны как [math]M1;[/math]
6. вершины шестой группы обозначены красным цветом и подписаны как [math]MIN;[/math]
7. синим дугам сопоставлены метки, отражающие данные, используемые в соответствующих жёлтых вершинах.

Рисунок 1. Граф фазы BUILD алгоритма.

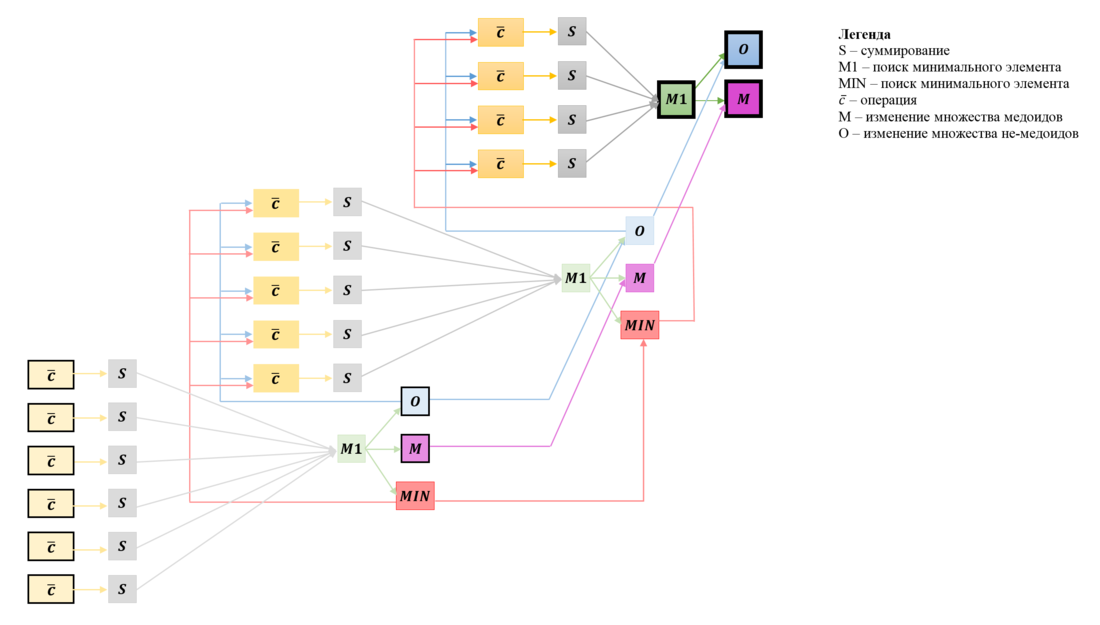
На Рис.2 представлен граф фазы BUILD для случая [math]n=6, k=3.[/math] Вершины, соответствующие операциям, получающим входные данные и производящим выходные данные, увеличены и выделены толстыми границами.

Рисунок 2. Граф фазы BUILD алгоритма для n = 6, k = 3.

1.7.2 Информационный граф фазы SWAP

Опишем граф фазы SWAP как аналитически, так и в виде рисунка.

Граф состоит из семи групп вершин:

1. Операция M, соответствующая первой группе вершин, осуществляет изменение множества медоидов.

   Единственная координата [math]It[/math] (номер итерации), соответствующая каждой из вершин, меняется в диапазоне [math][1; T),[/math] принимая все целочисленные значения, где:

   [math]T\in \N[/math] - количество выполнений фазы SWAP во время работы алгоритма PAM.

   Аргументами операции являются:

   • результат срабатывания операции, соответствующей вершине из седьмой группы с координатой [math]It,[/math]
   • [math]M_{It-1}[/math] - множество медоидов:
     • при [math]It = 1 [/math] - результат выполнения фазы BUILD;
     • при [math]1\lt It \lt T [/math] - результат срабатывания операции, соответствующей вершине из первой группы с координатой [math]It-1.[/math]

   Результат срабатывания операции является:

   • при [math]It \lt T -1 [/math] - промежуточным данным алгоритма;
   • при [math]It = T - 1[/math] - выходным данным фазы SWAP.

   
   

2. Операция O, соответствующая второй группе вершин, осуществляет изменение множества не-медоидов.

   Единственная координата [math]It[/math], соответствующая каждой из вершин, меняется в диапазоне [math][1; T),[/math] принимая все целочисленные значения, где:

   [math]T\in \N[/math] - количество выполнений фазы SWAP во время работы алгоритма PAM.

   Аргументами операции являются:

   • результат срабатывания операции, соответствующей вершине из седьмой группы с координатой [math]It,[/math]
   • [math]O_{It-1}[/math] - множество не-медоидов:
     • при [math]It = 1 [/math] - результат выполнения фазы BUILD;
     • при [math]1\lt It \lt T [/math] - результат срабатывания операции, соответствующей вершине из второй группы с координатой [math]It-1.[/math]

   Результат срабатывания операции является промежуточным данным алгоритма.

   
   

3. Операция, соответствующая третьей группе вершин, выглядит следующим образом:

   [math]\overline{a}=\overline{a}_{x_{m_i} } = \{ \min_{ x_{m_l} \in M \backslash \{x_{m_i}\} } \rho ( x_{m_l},x_j ) \| 1 \leq j \leq n \}.[/math]

   Координаты вершин:

   • [math]It[/math] - меняется в диапазоне [math][1; T],[/math] принимая все целочисленные значения;
   • [math]i[/math] - меняется в диапазоне [math][1; k],[/math] принимая все целочисленные значения.

   Аргументом операции является [math]\overline{x}_{m_i}:[/math]

   • при [math]It = 1[/math] - результат выполнения фазы BUILD;
   • при [math]It \gt 1[/math] - результат срабатывания операции, соответствующей вершине из первой группы с координатой [math]It-1.[/math]

   Результат срабатывания операции является промежуточным данным алгоритма.

   
   

4. Операция, соответствующая четвертой группе вершин, выглядит следующим образом:

   [math]\overline{b}=\overline{b}_{x_{m_i} x_{o_p} } = \{ \min (\overline{a}_{ x_{m_i}}^{(j)}, \rho ( x_{o_p},x_j )) \| 1 \leq j \leq n \}.[/math]

   Координаты вершин:

   • [math]It[/math] - меняется в диапазоне [math][1; T],[/math] принимая все целочисленные значения;
   • [math]i[/math] - меняется в диапазоне [math][1; k],[/math] принимая все целочисленные значения;
   • [math]p[/math] - меняется в диапазоне [math][1; n-k],[/math] принимая все целочисленные значения.

   Аргументами операции являются:

   • [math]\overline{x}_{o_p}:[/math]
     • при [math]It = 1[/math] - результат выполнения фазы BUILD;
     • при [math]It \gt 1[/math] - результат срабатывания операции, соответствующей вершине из второй группы с координатой [math]It-1[/math]
   • [math]\overline{a}_{x_{m_i}}[/math] - результат срабатывания операции, соответствующей вершине из третьей группы с координатами [math]It, i.[/math]

   Результат срабатывания операции является промежуточным данным алгоритма.

   
   

5. Операция S, соответствующая пятой группе вершин, выглядит следующим образом:

   [math]S = \sum_{j = 1}^{n} \overline {b}^{(j)}.[/math]

   Координаты вершин:

   • [math]It[/math] - меняется в диапазоне [math][1; T],[/math] принимая все целочисленные значения;
   • [math]i[/math] - меняется в диапазоне [math][1; k],[/math] принимая все целочисленные значения;
   • [math]p[/math] - меняется в диапазоне [math][1; n-k],[/math] принимая все целочисленные значения.

   Аргументами операции являются:

   • [math]\overline{b}_{x_{m_i} x_{o_p} }[/math] - результат срабатывания операции, соответствующей вершине из четвертой группы с координатами [math]It, i, p.[/math]

   Результат срабатывания операции является промежуточным данным алгоритма.

   
   

6. Операция M1, соответствующая шестой группе вершин, выглядит следующим образом:

   [math]M1 = (F_{x_{o_p}}^{It}; x_{o_p}),[/math] где [math] \begin{cases} F_{x_{o_p}}^{It} = \min_{x_{o_p} \in O} S & \quad\\ x_{o_p} = \arg F_{x_{o_p}}^{It} & \quad\\ \end{cases}[/math]

   Координаты вершин:

   • [math]It[/math] - меняется в диапазоне [math][1; T],[/math] принимая все целочисленные значения;
   • [math]i[/math] - меняется в диапазоне [math][1; k],[/math] принимая все целочисленные значения.

   Аргументами операции являются:

   • [math]S[/math] - результаты срабатывания операций, соответствующих вершинам из пятой группы с первыми двумя координатами [math]It, i,[/math] всего [math]n-k[/math] величин.

   Результат срабатывания операции является промежуточным данным алгоритма.

   
   

7. Операция M2, соответствующая седьмой группе вершин, выглядит следующим образом:

   [math]M2 = (F_{x_{o_p}, x_{m_i}}^{It}; x_{m_i}; x_{o_p}),[/math] где [math]\begin{cases} F_{x_{o_p}, x_{m_i}}^{It} = \min (\min_{x_{m_i} \in M} (F_{x_{o_p}}^{It}), M2_{It-1}) & \quad\\ x_{m_i} = \arg \min_{x_{m_i} \in M} M1 & \quad\\ \end{cases}[/math]

   Координаты вершин:

   • [math]It[/math] - меняется в диапазоне [math][1; T],[/math] принимая все целочисленные значения.

   Аргументами операции являются:

   • [math]M1 = (F_{x_{o_p}}^{It}; x_{o_p})[/math] - результаты срабатывания операций, соответствующих вершинам из шестой группы с координатами [math]It, i,[/math] всего [math]k[/math] величин;
   • [math]M2_{It-1}:[/math]
     • при [math]It = 1[/math] - результат выполнения фазы BUILD;
     • при [math]It \gt 1[/math] - результаты срабатывания операции, соответствующей вершине из седьмой группы с координатой [math]It-1;[/math]

   Результат срабатывания операции является:

   • при [math]It \lt T[/math] - промежуточным данным алгоритма;
   • при [math]It = T[/math] - выходным данным фазы SWAP.

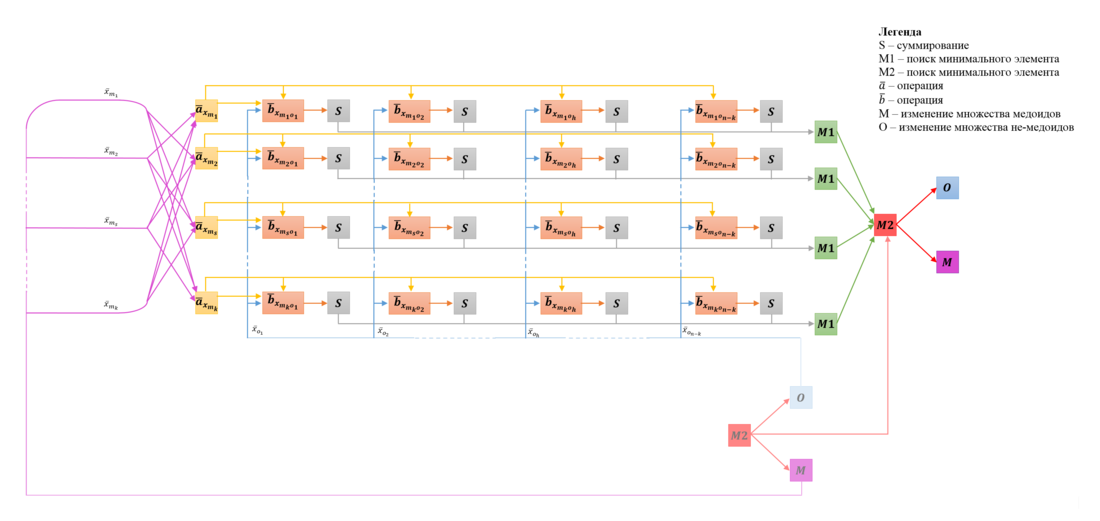
Описанный граф в общем случае представлен на Рис.3, отображена одна итерация фазы SWAP. Обозначения:

1. вершины первой группы обозначены фиолетовым цветом и подписаны как [math]M;[/math]
2. вершины второй группы обозначены синим цветом и подписаны как [math]O;[/math]
3. вершины третьей группы обозначены желтым цветом и подписаны как [math]\overline{a}_{x_{m_i} };[/math]
4. вершины четвертой группы обозначены оранжевым цветом и подписаны как [math]\overline{b}_{x_{m_i o_p} };[/math]
5. вершины пятой группы обозначены серым цветом и подписаны как [math]S;[/math]
6. вершины шестой группы обозначены зеленым цветом и подписаны как [math]M1;[/math]
7. вершины седьмой группы обозначены красным цветом и подписаны как [math]M2;[/math]
8. синим дугам сопоставлены метки, отражающие данные, используемые в соответствующих оранжевых вершинах;
9. фиолетовым дугам сопоставлены метки, отражающие данные, используемые в соответствующих жёлтых вершинах.

Рисунок 3. Граф фазы SWAP алгоритма.

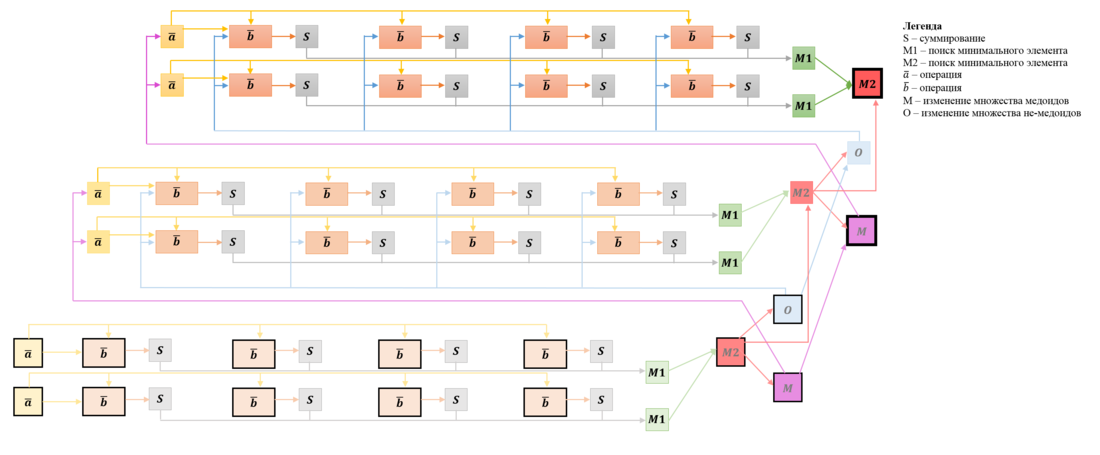
На Рис.4 представлен граф фазы SWAP для случая [math]n=6, k=2, T=3.[/math] Вершины, соответствующие операциям, получающим входные данные и производящим выходные данные, увеличены и выделены толстыми границами.

Рисунок 4. Граф фазы SWAP алгоритма для n = 6, k = 2, T = 3.

1.8 Ресурс параллелизма алгоритма

При параллельной реализации алгоритма PAM будем рассматривать параллельные варианты фазы BUILD и SWAP (возможная параллельная реализация). Покажем, что сложность фазы BUILD сопоставима со сложностью одной итерации фазы SWAP.

Оценки последовательной сложности фаз BUILD и SWAP приведены в параграфе "Последовательная сложность алгоритма".

1.8.1 Ресурс параллелизма фазы BUILD

Для решения задачи кластеризации методом PAM в параллельном варианте фазы BUILD в предположении доступности неограниченного числа процессов для одной итерации необходимо выполнить:

• 1 ярус с нахождением [math]\overline{c}:[/math]
  • [math]n[/math] операций нахождения минимального из двух элементов при [math]It \gt 1[/math];
• 1 ярус с нахождением суммы [math]S:[/math]
  • [math]n-1[/math] операцию сложения;
• 1 ярус с нахождением значений элемента [math]M1:[/math]
  • [math]n-It[/math] операций нахождения минимального из двух элементов;
• 1 ярус с нахождением минимального элемента [math]\overline{MIN}:[/math]
  • [math]n[/math] операций нахождения минимального из двух элементов при [math]It\gt 1;[/math]
• 1 ярус с изменением множеств медоидов и не-медоидов (не выполняются операции рассматриваемых типов).

Таким образом, параллельная сложность одного шага фазы BUILD равна:

• [math]n-1[/math] операция сложения;
• [math]n-It[/math] операций нахождения минимального из двух элементов при [math]It=1;[/math]
• [math]3n-It[/math] операций нахождения минимального из двух элементов при [math]It\gt 1.[/math]

Параллельная сложность фазы BUILD при числе кластеров [math]k[/math] равна:

• [math]kn-k[/math] операция сложения;
• [math]3kn - 2n - \frac{1}{2}k^2 - \frac{1}{2}k[/math] операций нахождения минимального из двух элементов.

В параллельном варианте, по сравнению с последовательным, при [math]k, n \to \infty[/math] количество операций на один порядок меньше по параметру [math]n:[/math]

[math]O(kn)[/math] против [math]O(kn^2).[/math]

Соотношение количества сложений и взятий минимума для фазы BUILD является постоянным и стремится к [math]3,[/math] при [math]k, n \to \infty.[/math]

Максимальная ширина яруса достигается при вычислении [math]\overline {c}[/math] и [math]S[/math] и равна [math]n-It+1[/math] для шага [math]It[/math] фазы BUILD. Максимальная ширина яруса при рассмотрении всей фазы есть [math]n[/math] и достигается на первом шаге.

1.8.2 Ресурс параллелизма фазы SWAP

Для решения задачи кластеризации методом PAM в параллельном варианте фазы SWAP в предположении доступности неограниченного числа процессов для одной итерации необходимо выполнить:

• 1 ярус с нахождением [math]\overline {a}:[/math]
  • [math]n(k-1)[/math] операций нахождения минимального из двух элементов;
• 1 ярус с нахождением [math]\overline {b}:[/math]
  • [math]n[/math] операций нахождения минимального из двух элементов;
• 1 ярус с нахождением суммы [math]S[/math]:
  • [math]n-1[/math] операцию сложения;
• 1 ярус с нахождением минимального элемента 'первого' вида [math](M1 = \min_{x_{o_p} \in O} S):[/math]
  • [math]n-k-1[/math] операцию нахождения минимального из двух элементов;
• 1 ярус с нахождением минимального элемента 'второго' вида [math](M2 = \min_{x_{m_i} \in M} M1):[/math]
  • [math]k-1[/math] операцию нахождения минимального из двух элементов;
• 1 ярус с изменением множеств медоидов и не-медоидов (не выполняются операции рассматриваемых типов).

Таким образом, параллельная сложность одной итерации фазы SWAP равна:

• [math]n-1[/math] - по количеству операций сложения;
• [math]kn + n - 2[/math] - по количеству операций нахождений минимума для двух чисел.

В параллельном варианте, по сравнению с последовательным, при [math]k, n \to \infty[/math] количество операций на один порядок меньше по параметру [math]n:[/math]

[math]O(kn)[/math] против [math]O(kn^2).[/math]

Соотношение количества сложений и взятий минимума для одной итерации фазы SWAP является постоянным и равным [math]k,[/math] при [math]n \to \infty[/math].

Максимальная ширина яруса достигается при вычислении [math]\overline {b}[/math] и [math]S[/math] и равна [math]k(n-k).[/math]

При использовании выбранной модели, в предположении доступности неограниченного числа вычислителей, фаза BUILD при [math]n \to \infty[/math] требует большего количества операций суммирования на порядок [math]k[/math], по сравнению с одной итерацией фазы SWAP. В свою очередь, количество операций подсчёта минимума ассимптотически эквивалентны.

1.9 Входные и выходные данные алгоритма

Входные данные:

• число [math]n[/math] - количество точек упорядоченного множества [math]X;[/math]
• число [math]k[/math] - количество требуемых кластеров;
• [math]n[/math] векторов, состоящих из [math]n-1[/math] вещественных чисел, - попарных расстояний между элементами из множества [math]X[/math] за исключением расстояний вида [math]\rho (x, x)=0, x \in X;[/math]

Объём входных данных: [math]n(n-1)[/math] вещественное число и [math]2[/math] целых числа.

Структура хранения данных:

• сразу после считывания входных данных составляется квадратная симметрическая матрица [math]D^{n * n}[/math], у которой каждый элемент [math]d_{ij}[/math] является вещественным числом - расстоянием [math]\rho (x_i, x_j);[/math]
• для множества медоидов [math]M[/math] создаётся массив из [math]k[/math] целых чисел - индексов принадлежащих ему элементов из множества [math]X[/math], аналогичный массив [math]n-k[/math] целых чисел создаётся для множества не-медоидов [math]O;[/math]
• для пересылки данных, как правило, используется тройка [math](F_{x_{m_s}, x_{o_h}}^{i_j}; x_{m_s}; x_{o_h})[/math] или пара [math](F_{x_{o_h}}^{i_j}; x_{o_h}),[/math] где:
  • [math]x_{m_s}[/math] - целое число, обозначающее порядковый номер элемента множества [math]X;[/math]
  • [math]x_{o_h}[/math] - целое число, обозначающее порядковый номер элемента множества [math]X;[/math]
  • [math]F_{x_{m_s}, x_{o_h}}^{i_j}[/math] - вещественное число, равное минимальному значению целевой функции, вычисленному в текущем контексте.

Выходные данные:

• [math]k[/math] целых чисел, составляющих множество [math]M;[/math]
• [math]1[/math] вещественное число, являющееся значением целевой функции.

Объём выходных данных:

• [math]k[/math] целых чисел и [math]1[/math] вещественное.

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности алгоритма является линейным и равным [math]n.[/math]

Вычислительная мощность последовательного алгоритма, как отношение числа операций к суммарному объему входных и выходных данных, равна [math]O(T*k).[/math] Вычислительная мощность параллельного алгоритма равна [math]O(T*\frac{k}{n}).[/math]

Алгоритм PAM является менее чувствительным к выбросам данных, чем алгоритм k-средних. Это связано с использованием медоидов, менее подверженных влиянию таких данных.

Фиксированный способ выбора начальных приближений позволяет говорить о воспроизводимости полученных результатов для последовательной реализации. Для параллельной работы алгоритма подобная воспроизводимость отсутствует, так как из-за недетерминированности выбора элементов, на которых достигается минимальное значение целевой функции для каждой итерации, итоговое множество медоидов и, следовательно, значение целевой функции может меняться.

Алгоритм PAM конечен, так как:

• количество операций фазы BUILD конечно;
• значение целевой фукнции неотрицательно и на каждой итерации фазы SWAP строго уменьшается.

Одно из преимуществ алгоритма PAM заключается в том, что он может работать с любой матрицей различий. В данном случае принципиальное отличие от матрицы расстояний заключается в том, что для матрицы различий может не выполняться неравенство треугольника, так как в основе её построения не обязательно используется метрика.

Основные операция алгоритма PAM: сложение и нахождение минимума. Операция взятия минимума не подвержена процессу накопления ошибки. На каждой итерации алгоритма сложение производится над значениями, взятыми непосредственно из исходных данных. Таким образом, алгоритм PAM не накапливает ошибок в процессе своей работы и является устойчивым.

При [math]k(n-k) \, \bmod \, p \neq 0[/math] отсутствует возможность равномерно распределить задачи рассчёта [math]\overline{b}[/math] между процессами. Кроме того, если [math]k \, \bmod \, p \neq 0[/math], то после их распределения для некоторых процессов окажется необходимым вычислить несколько соседних значений [math]\overline{a}.[/math] Таким образом, равномерная загрузка процессов не всегда возможна. Помимо этого, агрегирование данных с целью вычисления глобального минимума приводит к простою незадействованных процессов.

Как и большинство алгоритмов кластеризации, PAM может сходиться к некоторому локальному минимуму, не совпадающему с глобальным.

В силу квадратичной сложности последовательного алгоритма, его эффективность при использовании на больших объемах данных достаточно низкая. Алгоритм эффективен при работе с данными небольшого объема.

2 Программная реализация алгоритма

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.3.1 Возможная параллельная реализация алгоритма PAM

Необходимость уменьшения времени решения задачи приводит к потребности в создании паралельной реализации алгоритма. В дальнейшем будем придерживаться следующих допущений:

• возможно использование [math]p[/math] процессов;
• не нарушая общности суждений, множества [math]M, O[/math] - упорядоченны.

Приведённые далее возможные схемы для параллельных реализаций фазы BUILD и фазы SWAP основаны на максимально равномерном распределении задач между процессами.

2.3.1.1 Возможная параллельная реализация фазы BUILD

Главная задача заключается в распараллеливании многочисленных вычислений целевой функции на каждой итерации фазы BUILD:

[math]F^i = \min_{x_{o_h} \in O_{i-1}} F_{x_{o_h}}^i,[/math] где [math]F_{x_{o_h}}^i = \sum_{j = 1}^{n} \overline{MIN}_{i, x_{o_h}}^{(j)},[/math] где

[math]\overline{MIN}_{1, x_{o_h} \in O_0} = \{ \rho (x_{o_h}, x_j ) \| 1 \leq j \leq n \};[/math]

[math]\overline{MIN}_{i, x_{o_h} \in O_{i-1}} = \{ \min ( \overline{MIN}_{i-1, x_{m_{i-1}}}^{(j)}, \rho (x_{o_h}, x_j) ) \| 1 \leq j \leq n \}, \forall i: 1 \lt i \leq k.[/math]

Схема реализации:
(далее [math]0 \lt i \leq k [/math] - номер текущей итерации)

1. для каждого процесса с номером [math]j[/math] [math](0 \leq j \lt p):[/math]
   1. положим:

      [math]pos = p-(n-i+1) \, \bmod \, p;[/math]

   2. на каждой итерации процессу необходимо вычислить [math]r_j[/math] значений целевой функции для соответствующих ему элементов [math]x_{o_h}, ..., x_{o_{h+(r_j-1)}}:[/math]

      [math] r_j = \begin{cases} \lfloor \frac{n-i+1}{p} \rfloor , 0 \leq j \lt pos & \quad\\ \lceil \frac{n-i+1}{p} \rceil , pos \leq j & \quad\\ \end{cases} [/math]

      [math]h = \begin{cases} r_j*j , 0 \leq j \lt pos & \quad\\ (r_j-1)*pos + (j-pos)*r_j , pos \leq j & \quad\\ \end{cases}[/math] - порядковый номер [math]x_{o_h};[/math]

2. каждому процессу с номером [math]j[/math] [math](0 \leq j \lt p):[/math]
   1. найти минимум среди значений целевой функции [math]F_{x_{o_h}}^i[/math] для каждого из значений параметра [math]x_{o_h};[/math]
      • в данном случае может быть использована оптимизация, описанная в вычислительном ядре алгоритма;
   2. для процессов с номером [math]j \neq 0[/math] переслать процессу с номером [math]0[/math] пару [math](x_{o_h}, F_{x_{o_h}}^i)[/math] для всех обработанных [math]x_{o_h};[/math]

3. для процесса с номером [math]0[/math]:
   1. принять пары от процессов [math](0, p-1],[/math] в ответ на шаг 2.2;
   2. найти [math]x_{o_h},[/math] для которого целевая функция принимает минимальное значение, и положить [math]x_{m_i}:=x_{o_h};[/math]
   3. вычислить [math]\overline{MIN}_{i, x_{m_i}}[/math];
   4. разослать пару [math](x_{m_i}, \overline{MIN}_{i, x_{m_i}})[/math] при помощи широковещательной рассылки;

4. для каждого процесса с номером [math]j[/math] [math](0 \leq j \lt p):[/math]
   1. принять пару [math](x_{m_i}, \overline{MIN}_{i, x_{m_i}})[/math] в ответ на шаг 3.4;
   2. скорректировать локальные копии множеств [math]M[/math] и [math]O[/math], изменив принадлежность вектора [math]x_{m_i}[/math], а также обновить хранимое значение вектора [math]\overline{MIN}[/math] для подготовки к следующей итерации;
   3. перейти к шагу 2.1.

После завершения [math]k[/math] шагов фазы BUILD, множества [math]M[/math] и [math]O[/math] (одинаковые для каждого процесса согласно приведенной схеме), а так же значение целевой функции являются выходными данными фазы BUILD.

2.3.1.2 Возможная параллельная реализация фазы SWAP

Главная задача заключается в распараллеливании многократного вычисления целевой функции на каждой итерации фазы SWAP:

[math]F^i = \min_{x_{m_s} \in M_{i-1} } \min_{x_{o_h} \in O_{i-1}} \sum_{j = 1}^{n} \min ( \min_{ x_{m_l} \in M_{i-1} \backslash \{x_{m_s}\} } ( \rho ( x_{m_l},x_j )) , \rho ( x_{o_h},x_j) )[/math]

Схема реализации:
(далее [math]i \in \N[/math] - номер текущей итерации)

1. для каждого процесса с номером [math]j[/math] [math](0 \leq j \lt p):[/math]
   1. положим:

      [math]pos = p-(k*(n-k)) \, \bmod \, p;[/math]

   2. на каждой итерации процессу необходимо вычислить [math]r_j[/math] значений целевой функции для соответствующих ему пар вида (медоид, не-медоид) [math](x_{m_s}, x_{o_h}), (x_{m_s}, x_{o_{h+1}}), ..., (x_{m_s}, x_{o_{n-k}}), (x_{m_{s+1}}, x_{o_0}), (x_{m_{s+1}}, x_{o_1}), . . . \, : [/math]

      [math] r_j = \begin{cases} \lfloor \frac{k*(n-k)}{p} \rfloor , 0 \leq j \lt pos & \quad\\ \lceil \frac{k*(n-k)}{p} \rceil , pos \leq j & \quad\\ \end{cases} [/math]

      [math]s = \begin{cases} (r_j*j) \mbox{ div } (n-k) , 0 \leq j \lt pos & \quad\\ ((r_j-1)*pos + r_j*(j-pos)) \mbox{ div } (n-k), pos \leq j & \quad\\ \end{cases}[/math] - порядковый номер [math]x_{m_s};[/math]

      [math]h = \begin{cases} (r_j*j) \, \bmod \, (n-k) , 0 \leq j \lt pos & \quad\\ ((r_j-1)*pos + r_j*(j-pos)) \, \bmod \, (n-k), pos \leq j & \quad\\ \end{cases}[/math] - порядковый номер [math]x_{o_h};[/math]

2. каждому процессу с номером [math]j[/math] [math](0 \leq j \lt p):[/math]
   1. найти минимум среди вычисленных значений целевой функции для каждого из значений первого параметра [math]x_{m_s}[/math] по соответствующим ему [math]x_{o_h};[/math]
      • в данном случае может быть использована оптимизация, описанная в вычислительном ядре алгоритма;
   2. переслать процессу с номером [math]N = s \, \bmod \, p[/math] (если [math]N \neq j[/math]) тройку [math](F_{x_{m_s}, x_{o_h}}^{i_j}, x_{m_s}, x_{o_h})[/math] для всех обработанных [math]x_{m_s};[/math]
3. для процессов с номерами [math]j\lt \min (p, k):[/math]
   1. принять описанные выше тройки от процессов, обработавших элементы [math]x_{m_{z \, \bmod \, p = j}}, z = \overline {0, k-1},[/math] в ответ на шаг 2.2;
   2. вычислить минимальное среди полученных значений целевой функции;
   3. запомнить [math]x_{m_s}[/math] и [math]x_{o_h}[/math], на которых минимальное значение было достигнуто;
   4. при [math]j \neq 0 [/math] отправить тройку [math](F_{x_{m_s}, x_{o_h}}^{i_j}, x_{m_s}, x_{o_h})[/math], соответствующую выбранной паре, процессу с номером [math]0[/math];
4. для процесса с номером [math]0[/math]:
   1. принять тройки от процессов [math](0, min(k-1, p-1)],[/math] в ответ на шаг 3.4;
   2. найти пару [math](x_{m_s}, x_{o_h})[/math], для которой целевая функция принимает минимальное значение;
   3. сравнить найденное минимальное значение с вычисленным значением целевой функции на предыдущей итерации фазы SWAP;
      1. ( условие останова ) если значение целевой функции не уменьшилось, остановить вычисление;
      2. иначе, разослать выявленную пару [math](x_{m_s}, x_{o_h})[/math] при помощи широковещательной рассылки;
5. для каждого процесса с номером [math]j[/math] [math](0 \leq j \lt p):[/math]
   1. принять пару [math](x_{m_s}, x_{o_h})[/math] в ответ на шаг 4.3.2;
   2. скорректировать локальные копии множеств [math]M[/math] и [math]O[/math], заменяя элемент [math]x_{m_s}[/math] на элемент [math]x_{o_h}[/math] и наоборот;
   3. перейти к шагу 2.

2.3.1.3 Ограничения и недостатки

Ограничения:

• предполагается, что матрица расстояний [math]D^{n * n}[/math] полностью помещается в памяти каждого процесса.

Недостатки:

• при распределении обсчитываемых целевых функций, каждому из процессов ставится в соответствие некоторая совокупность пар [math](x_{m_s}, x_{o_h})[/math], для которых нужно рассчитать значения целевой функции. В случае, если количество процессов не кратно количеству обрабатываемых кластеров, различные процессы получат пары у которых совпадают [math]x_{m_s}[/math], что приведёт к совершению одинаковых вычислений на различных процессах: [math] \min_{ x_{m_l} \in M_{i-1} \backslash \{x_{m_s}\} } ( \rho ( x_{m_l},x_j )), 1 \leq j \leq n;[/math]
• вычисление фазы SWAP успешно распараллеливается между [math]p[/math] процессами, однако после этого происходит агрегация данных в 2 этапа относительно [math](x_{m_s}, x_{o_h})[/math] для вычисления глобального минимума. На первом этапе данные собираются на первых [math]\min (p,k)[/math] процессах, где происходят локальные вычисления минимумов среди принятых данных (для каждого [math]x_{m_s}[/math]), после чего полученные минимумы и связанная с ними информация агрегируются на мастер-процессе, который вычисляет глобальный минимум и извещает о нём все остальные процессы.
  Во время описанных вычислений все незадействованные процессы простаивают.

Дополнительные возможности:

• помимо описанной схемы, также есть возможность распараллелить операцию вычисления матрицы расстояний [math]D[/math], однако это является отдельной алгоритмической задачей и не даёт существенного прироста производительности алгоритма.

2.3.2 Существующие параллельные реализации алгоритма PAM

Примером другой параллельной реализации алгоритма PAM может служить реализация в пакете SPRINT для языка R (подробнее см. существующие реализации алгоритма).

2.4 Масштабируемость алгоритма и его реализации

Структура графа алгоритма (см. 1.7 Информационный граф алгоритма) такова, что позволяет надеяться на получение хорошей масштабируемости.

Исследование масштабируемости параллельной реализации алгоритма Partitioning Around Medoids проводилось на суперкомпьютере BlueGene/P . Отметим, что для данному суперкомпьютеру свойственна стабильность по времени вычисления одной и той же задачи при различных запусках. Во время вычислений каждому MPI процессу соответствовало 1 ядро процессора PowerPC 450, 850 MHz с пиковой производительностью 3.4 GFlop/sec per core.

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

• число процессов (p):
  • [1; 4 : 512] с шагом 4 процесса;
• размер кластеризуемого множества (n):
  • [4; 16; 32; 64];
  • [128 : 3200] с шагом 128 элементов;
• каждому размеру кластеризуемого множества соответствует количество кластеров для разбиения (k):
  • [2; 4; 4; 8];
  • [2 : 50] с шагом 2.

Особенности проведения эксперимента:

• тестовые данные являются псевдослучайными;
• для всех экспериментов использовался одинаковый набор данных;
• в соответствии с описанными параметрами запуска, для множеств размерности [128 : 3200], количество кластеров (k) прямо пропорционально размеру задачи (n).

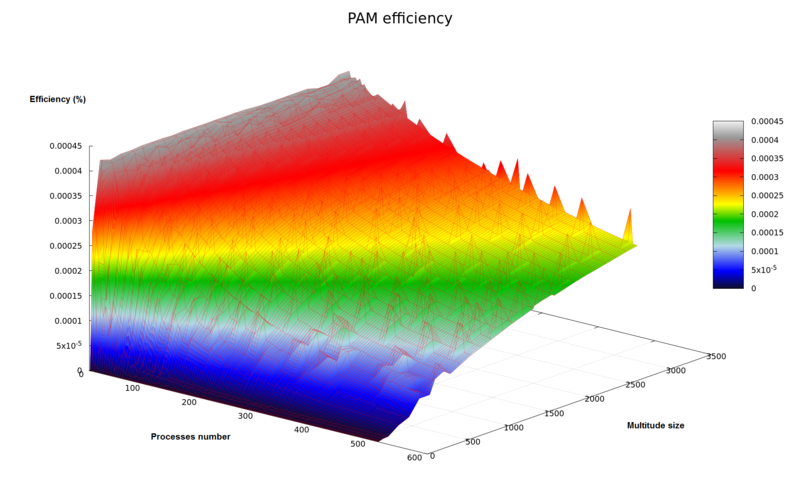
В результате проведённых экспериментов был получен широкий диапазон эффективности реализации алгоритма:

• минимальная эффективность реализации: [math]3.4 * 10^{-9} \, %[/math] достигается при использовании 512 процессов для множества из 4 элементов и 2-х кластеров (результат вызван избыточностью количества процессов по отношению к размеру задачи);
• максимальная эффективность реализации: [math]4.1 * 10^{-4} \, %[/math] достигается при использовании 4 процессов для множества из 128 элементов и 2 кластеров.

Абсолютная величина производительности алгоритма (GFlops) определялась как количество операций с плавающей точкой за секунду. Точное количество операций было вычислено на основании последовательной сложности алгоритма, целочисленные операции и операции работы с памятью не учитывались.

Таким образом, производительность обусловлена как самим алгоритмом (его внутренняя структура определяет соотношение между операциями работы с памятью, операциями над целочисленными значениями и значениями с плавающей точкой), так и используемой реализацией.

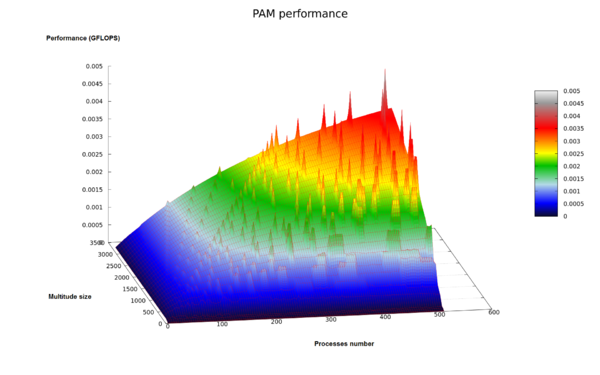
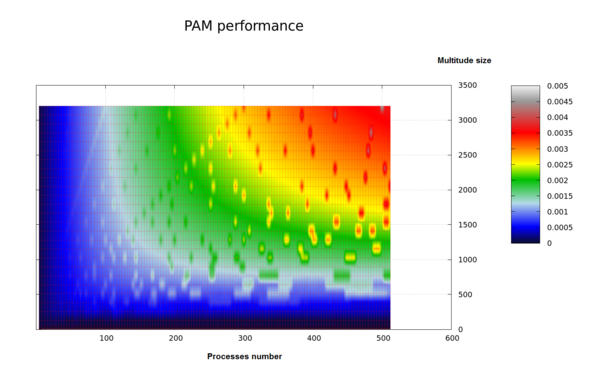
На следующих рисунках приведены графики производительности и эффективности выбранной реализации PAM в зависимости от изменяемых параметров запуска:

Рисунок 5а. Параллельная реализация алгоритма PAM. Изменение производительности в зависимости от числа процессов и размера множества.

Рисунок 5б. Параллельная реализация алгоритма PAM. Изменение производительности в зависимости от числа процессов и размера множества. Вид сверху.

Рисунок 6. Параллельная реализация алгоритма PAM. Изменение эффективности в зависимости от числа процессов и размера множества.

На рисунке 5б, видно, что пики организованы в прямые. Это обусловлено инвариантностью величины [math]a[/math] в соответствии с описанной в вычислительном ядре фазы SWAP оптимизацией. На рисунке 3 для информационного графа фазы SWAP наглядно видно, что при построчном распределении вычислений [math]\overline{b}_{x_{m_s, o_h}}[/math] возможно возникновение следующих ситуаций (далее при k * (n-k) mod p == 0 обозначим r = k * (n-k) / p ):

1. при r < (n-k) , если (n-k) mod r == 0 , то каждому процессу необходимо вычислить ровно одну величину [math]\overline{a}_{x_{m_s}};[/math]
2. при r ≥ (n-k) , если k mod p == 0 , то каждому процессу необходимо вычислить несколько соответствующих ему величин [math]\overline{a}_{x_{m_s}},[/math] при этом каждая величина будет вычислена ровно в одном процессе;
3. в остальных случаях вычисления величин [math]\overline{b}_{x_{m_s, o_h}}[/math] распределяются между процессами таким образом, что часть процессов обрабатывает больше величин [math]\overline{a}_{x_{m_s}}[/math] нежели остальные (ситуация возникает при обработке процессом последних элементов одной строки и первых элементов следующей). Подобная ситуация приводит к дополнительным вычислениям на некоторых процессах и, как следствие, к простою остальных, в связи с чем происходит падение производительности.

Первые два случая приводят к равномерному распределению нагрузки между процессами, и им соответствуют видимые пики на приведённых рисунках 5a, 5б, 6. Для 3-го случая из-за неравномерной загрузки процессов достигаемая производительность падает.

Второй случай соответствует размеру задачи меньшему, чем количество процессов и на практике маловероятен. Таким образом, для повышения производительности следует выбирать количество процессов так, чтобы k * (n-k) и (n-k) были кратны p и k * (n-k) div p соответственно.

Для исследуемой реализации, вычисление величин [math]\overline{a}_{x_{m_s}}[/math] может быть оптимизировано (за счёт распределения между процессами и последующих пересылок). Однако принципиальный вид графиков останется тем же: пики будут наблюдаться для случаев равномерного распределения вычислительных задач между процессами.

Построим оценки масштабируемости выбранной реализации алгоритма PAM:

• По числу процессов: [math]- \, 1.6 * 10^{-8}.[/math] С ростом числа процессов эффективность на рассмотренной области изменений параметров запуска уменьшается. Этот результат вызван ростом времени, затрачиваемого на пересылку данных, то есть ростом накладных расходов на организацию параллельного выполнения.
• По размеру задачи: [math]3.9 * 10^{-7}[/math]. С ростом размера задачи эффективность на рассмотренной области изменений параметров запуска увеличивается. Этот результат вызван увеличением количества вычислений относительно объема пересылок данных.
• Общая оценка масштабируемости: [math]- \, 1.2 * 10^{-9}[/math]. При рассмотрении области параметров запуска в целом можно говорить о том, что с ростом размера задачи и числа процессов эффективность незначительно падает.

Исследованная параллельная реализация на языке C++ (реализация написана самостоятельно)

2.7 Существующие реализации алгоритма

1. Последовательная реализация алгоритма PAM в пакете ClusterR на языке R:
   • Лицензия: MIT
   • веб-страница фреймворка (исходный код, системные требования и справочное руководство)
   • Алгоритм PAM реализован в функции 'Cluster_Medoids'. Отличительная особенность реализации :
     • для задания метрики между элементами кластеризуемого множества передаётся строка, задающая одну из реализованных в алгоритме метрик. Данный подход теряет одно из преимуществ алгоритма PAM, позволяющее в качестве матрицы расстояний использовать произвольную матрицу различий.

2. Последовательная реализация алгоритма PAM в пакете Cluster на языке R:
   • Лицензия: GPL (≥2)
   • веб-страница фреймворка (исходный код, системные требования и справочное руководство)
   • Алгоритм PAM реализован в функции 'pam()'. Данная реализация имеет следующие особенности :
     • функция может принимать на вход не множество точек, а матрицу расстояний между ними;
     • реализация более гибкая, так как принимает на вход матрицу различий элементов, а не использует какую-либо метрику;
     • может быть предоставлено графическое отображение.

3. Параллельная реализация алгоритма PAM в пакете SPRINT (Simple Parallel R INTerface - параллельный фреймворк) на языке R:
   • Лицензия: GPL (≥3)
   • веб-страница фреймворка (исходный код, системные требования и справочное руководство)
   • Алгоритм PAM реализован в фукции 'ppam()'. Входные параметры данной функции схожи с параметрами, задаваемыми в линейной реализации 'pam()' пакета Cluster языка R. Отличительной особенностью является подача на вход предвычисленной матрицы расстояний (например, с помощью функции 'pcor()' из этой же библиотеки).

4. Параллельная реализация алгоритма PAM на основе операций MapReduce на Hadoop кластере.
   • В рамках исследования по ускорению анализа информации о геноме были созданы реализации алгоритма PAM с использованием технологии MPI и технологии MapReduce. Реализация в открытом досупе отсутствует.