Участник:Denemmy/Partitioning Around Medoids (Алгоритм)

Эта работа успешно выполнена Преподавателю: в основное пространство, в подстраницу Данное задание было проверено и зачтено. Проверено Dexter и Zhum.

Partitioning Around Medoids
Последовательный алгоритм
Последовательная сложность	[math]O(T*K*N^2)[/math]
Объём входных данных	[math] N*(N-1)/2 + 2 [/math]
Объём выходных данных	[math] N [/math]

Авторы: Галеев Д.Ф, Запутляев И.

Оба автора в равной мере участвовали в написании, обсуждении и оформлении содержимого статьи.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Кластеризация - это задача из области машинного обучения, которая заключается в том, что нужно выделить некоторое число групп в исходном множестве, в каждой из которых содержатся схожие по некоторой метрике элементы.

Алгоритм Partitioning Around Medoids (PAM) был создан Леонардом Кауфманом (Leonard Kaufman) и Питером Руссивом (Peter J. Rousseeuw). и он очень похож на алгоритм K-means, в основном потому, что оба являются алгоритмами кластеризации, другими словами, оба разделяют множество объектов на группы (кластеры) и работа обоих основана на попытках минимизировать ошибку, но PAM работает с медоидами - объектами, являющимися частью исходного множества и представляющими группу, в которую они включены, а K-means работает с центроидами - искусственно созданными объектами, представляющими кластер.

Алгоритм PAM разделяет множество из N объектов на K кластеров, где и множество объектов, и число K являются входными данными алгоритма. Алгоритм работает с матрицей расстояний, его цель - минимизировать расстояние между представителями каждого кластера и его членами. Алгоритм использует следующую модель для решения задачи:

[math]F(x)=minimize \sum_{i=1}^{N}\sum_{j=1}^{N} d(i,j)z_{ij}[/math]

При этом:

1. [math] \sum_{i=1}^N {z_{ij} = 1} , j = 1,2,...,N[/math];

2. [math]z_{ij} \le y_i , i, j = 1,2,...,N[/math];

3. [math]\sum_{i=1}^N {y_i = K} , K - [/math] число кластеров;

4. [math]y_i , z_{ij} \in \{ 0,1 \} , i, j = 1,2,...,N[/math].

где функция [math]F(x)[/math] - целевая минимизируемая функция, [math]d(i,j)[/math] - мера расстояния между объектами [math]i[/math] и [math]j[/math], [math]z_{ij}[/math] - переменная, которая гарантирует, что расстояние только между объектами из одного кластера будет вычислено в целевой функции. Остальные выражения являются следующими ограничениями:

1. Каждый объект принадлежит одному и только одному кластеру;

2. Каждый объект относится к медоиде, представляющей его кластер;

3. Есть в точности K кластеров;

4. Решающая переменная принимает значения 0 или 1.

PAM может работать с двумя типами входных данных:

1. С матрицей объектов и значениями ее переменных;

2. С матрицей расстояний.

Алгоритм имеет две фазы:

Фаза Build:

1. Выбрать K объектов в качестве медоид;

2. Построить матрицу расстояний, если она не была задана;

3. Отнести каждый объект к ближайшей медоиде;

Фаза Swap:

4. Для каждого кластера найти объекты, снижающие среднее расстояние, и если такие объекты есть, выбрать те, которые снижают его сильней всего, в качестве медоид;

5. Если хотя бы одна медоида поменялась, вернуться к шагу 3, иначе завершить алгоритм.

1.2 Математическое описание алгоритма

Обозначения:

1. [math]M = \{ x_{m_1}, x_{m_2}, ... , x_{m_s} \} - [/math] множество медоид;

2. [math]L = \{ x_{l_1}, x_{l_2}, ... , x_{m_t} \} - [/math] множество объектов [math]x_i[/math], не являющихся медоидами;

3. [math]F_{M,L} = \sum_{j = 1}^{N} \min_{ x_{m_q} \in M} d(x_{m_q},x_{l_j}) - [/math] целевая функция.

Входные данные:

1. Множество [math]X = \{ x_{1}, x_{2}, \dots, x_{N} \}[/math] объектов [math]x_i[/math], каждый из который задается [math]P[/math] вещественными значениями;

2. Симметрическая матрица [math]D[/math], элементы [math]d_{ij} = d(x_i,x_j)[/math] которой являются расстояниями между объектами [math]x_i[/math] и [math]x_j[/math];

3. Число кластеров [math]K \le N[/math];

4. Метрика [math]d_{ij} = d(x_i,x_j)[/math], задающая расстояние между объектами [math]x_i[/math] и [math]x_j[/math].

Вычислительные формулы метода:

Фаза Build:

Представляет из себя выбор K медоид за K последовательных шагов:

1. [math]M_0 = \varnothing, L_0 = X[/math];

2. [math]x_{m_i} = \arg \min_{x_{l_q} \in L_0} \sum_{j = 1}^N d(x_{l_q},x_j), L_1 = L_0 \backslash \{x_{m_i}\}, M_1 = M_1 \cup \{x_{m_i}\}, i=1 \dots N [/math];

Фаза Swap:

Представляет из себя итерационный процесс.

1. Начальное приближение: [math]M_0 = M_{BUILD}, L_0 = L_{BUILD}[/math];

2. Множественные вычисления значений целевой функции для различных вариантов замены текущей медоиды на новую:

[math]F = arg \min_{i \in M , j \in L} \sum_{y \in L \backslash \{j\}} {min (d(i,y),d(j,y))} [/math];

3. Изменение множеств в соответствии с выбранной парой [math](x_{m_t}, x_{l_q})[/math]:

[math]M_i = M_{i-1} \backslash \{x_{m_t}\} \cup \{x_{l_q}\} , L_i = L_{i-1} \cup \{x_{m_t}\} \backslash \{x_{l_q}\} [/math];

4. Проверка критерия останова.

Выходные данные:

1. [math]M = \{ x_{m_{1}}, x_{m_{2}}, ..., x_{m_{K}} \}[/math] - множество медоид;

2. [math]K_{m_i} = \{ x_{l_q} \in L \| x_{m_i} = \arg \min_{x_{m_s} \in M} d(x_{l_q}, x_{m_s}) \}, i=1 \dots K, K -[/math] множество искомых кластеров.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма PAM сосредоточено в стадии SWAP и состоит из вычислений значений целевой функции для различных вариантов замены текущей медоиды на новую:

[math]F = arg \min_{i \in M , j \in L} \sum_{y \in L \backslash \{j\}} {min (d(i,y),d(j,y))} [/math]

1.4 Макроструктура алгоритма

Если на вход алгоритма была подана не матрица расстояний, а матрица объектов с их координатами в пространстве [math]R^P[/math], то операция вычисления расстояния между объектами [math]a[/math] и [math]b[/math] размерности [math]P[/math] будет являться макрооперацией. В качестве меры расстояния может быть использована евклидова метрика: [math] d(a,b) = \sqrt{\sum_{i=1}^P (a_i-b_i)^2}[/math]

1.5 Схема реализации последовательного алгоритма

Псевдокод алгоритма

1  функция PAM(D, k, tmax=100):
2      # D - матрица расстояний, k - число кластеров, tmax - маскимальное число итераций
3      выполнить фазу BUILD, получить множество метоидов M и множество не-метоидов L
4      вычислить значение целевой функции F
5      для t = 0..tmax-1:
6          выполнить фазу SWAP, вычислить значение целевой функции F'
7          delta = F - F'
8          если delta > 0:
9              обновить множества M и L
10             F = F'
11         иначе:
12             выйти из цикла
13     вернуть М

1.6 Последовательная сложность алгоритма

Обозначим количество кластеров как [math]K[/math], количество объектов как [math]N[/math], число итераций алгоритма как [math]T[/math].

На стадии BUILD каждый шаг нахождения очередного метоида имеет сложность [math]O(N^2)[/math] по количеству операций сложения вещественных чисел и по количеству операций сравнения двух вещественных чисел.
Тогда стадия BUILD имеет сложность [math]O(K*N^2)[/math]

На стадии SWAP вычисление целевой функции имеет сложность [math]O(K*N^2)[/math] по количеству операций сложения вещественных чисел и по количеству операций сравнения двух вещественных чисел.

Таким образом алгоритм PAN имеет сложность [math]O(T*K*N^2)[/math]

1.7 Информационный граф

Фаза BUILD

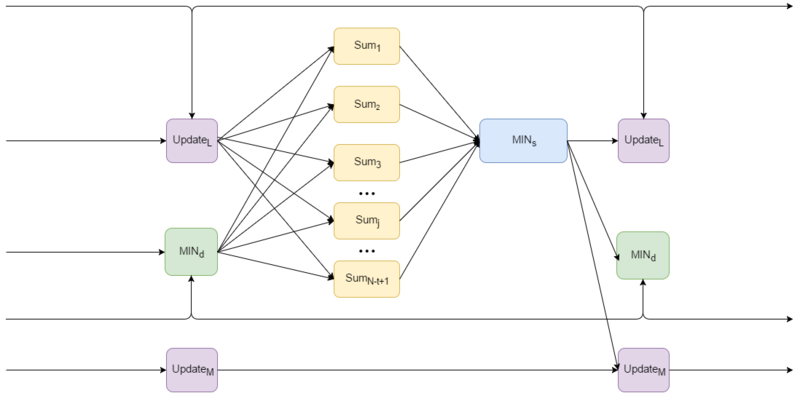
Общий вид информационного графа для шага t представлен на рисунке 1:

Рисунок 1. Информационный граф шага t фазы BUILD алгоритма.

Операции

• Update[math]_M[/math] и Update[math]_L[/math] - операции обновления множества метоидов и не-метоидов соответственно
• SUM - вычисление функции ошибки, на вход подается расстояния от очередного объекта до всех остальных, а также минимальные расстояния от выбранных на данном шаге метоидов до всех остальных вершин
• MIN[math]_s[/math] - нахождение аргумента, соответствующего минимальному значению, а также само минимальное значение
• MIN[math]_d[/math] - нахождение минимальных расстояний от медоидов до остальных вершин, используется в операции SUM

Количество шагов t равно K, где K - число кластеров

Фаза SWAP

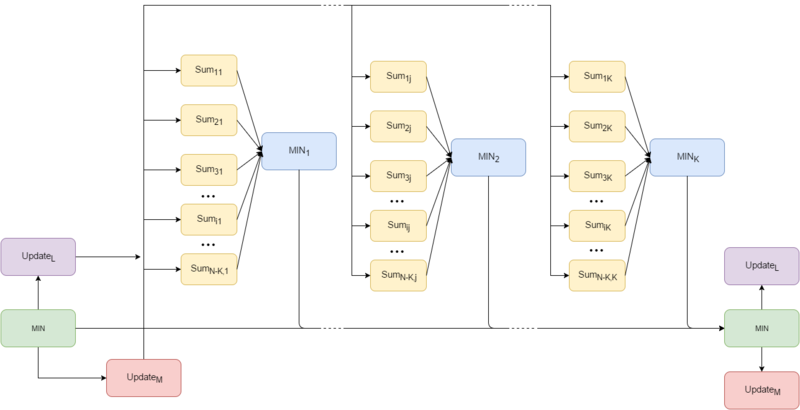
Общий вид информационного графа для итерации t представлен на рисунке 2:

Рисунок 2. Информационный граф итерации t фазы SWAP алгоритма.

Операции

• Update[math]_M[/math] и Update[math]_L[/math] - операции обновления множества метоидов и не-метоидов соответственно
• SUM - вычисление целевой функции
• MIN - нахождение аргумента, соответствующего минимальному значению, а также само минимальное значение

1.8 Ресурс параллелизма алгоритма

Пусть число кластеров равно [math]K[/math], а число объектов равно [math]N[/math]. Тогда параллельная сложность фазы BUILD имеет [math]O(K*N)[/math] операций сложения и [math]O(K*N)[/math] операций сравнения двух вещественных чисел. Таким образом параллельная сложность фазы BUILD равна [math]O(K*N*T)[/math].

Параллельная сложность фазы SWAP имеет [math]O(K*N)[/math] операций сложения и [math]O(K*N)[/math] операций сравнения двух вещественных чисел. Параллельная сложность фазы SWAP равна [math]O(K*N*T)[/math].

Таким образом параллельная сложность алгоритма равна [math]O(K*N*T)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные:

* число [math]K[/math] - количество кластеров;
* число [math]N[/math] - количество объектов;
* вектор попарных расстояний, имеющий длину [math]N*(N-1)/2[/math], из данных чисел однозначно восстанавливается симметрическая матрица расстояний [math]D[/math]

Объём входных данных: [math]N*(N-1)/2[/math] вещественное число и [math]2[/math] целых числа.

Выходные данные:

* K чисел [math]m_1, m_2, ..., m_K[/math] - индексы объектов соответствующие метоидам;
* N-K чисел [math]k_1, k_2, ..., k_{N-K}[/math] - номера кластеров для каждого объекта (кроме тех, что являются метоидами);

Объём выходных данных: [math]N[/math] целых чисел.

1.10 Свойства алгоритма

Вычислительная мощность

Суммарный объем входных данных равен [math] O(N^2) [/math] , число операций алгоритма PAM равно [math] O(K*N^2*\Tau) [/math], где [math]K[/math] – число кластеров, [math]\Tau[/math] – число итераций алгоритма, [math] N [/math] - число точек. Тогда вычислительная мощность алгоритма PAM равна [math]O(K*\Tau)[/math].

Детерминированность и Устойчивость

Алгоритм PAM является итерационным, количество итераций может быть ограничено сверху, однако в общем случае не фиксируется. Из-за недетермирированности выбора элементов, на которых достигается минимум целевой функции, алгоритм не является детермирированным. Однако, данный алгоритм является устойчивым, поскольку не накапливает ошибки в процессе своей работы.

Сильные стороны алгоритма:

• Меньшая чувствительность к выбросам, чем k-means
• Несложность реализации

• Возможность распараллеливания

  Однако равномерная загрузка процессоров не всегда возможна.

Недостатки алгоритма:

• Квадратичная сложность алгоритма

• Количество кластеров является параметром алгоритма

  Во многих задачах число кластеров может быть неизвестным.

• Возможность сходимости к локальному оптимуму

  Оптимальное решение не гарантировано.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Исследование проводилось на суперкомпьютере "Ломоносов" . Аппаратные характеристики суперкомпьютера. Алгоритм реализован с использованием технологии MPI.

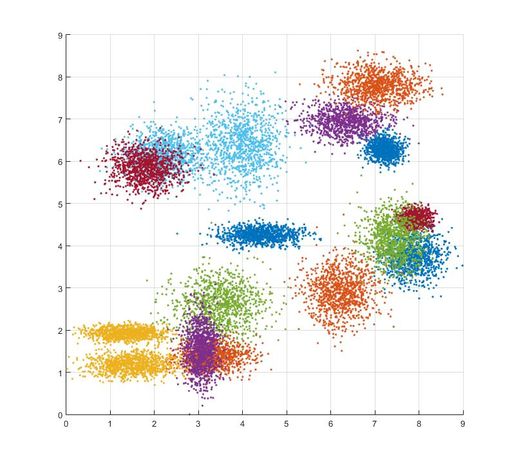
Данные были сгенерированы в Matlab'е случайным образом. Количество кластеров равно 16, каждый кластер был промоделирован нормальным распределением с некоторыми случайными значениями среднего и среднеквадратического отклонения. Размерность данных равна 2, а число точек на каждый кластер было достаточно большим для проведения экспериментов с различными значениями размерности матрицы расстояний. Пример сгенерированных данных показан на рисунке 3.

Рисунок 3. Пример сгенерированных данных.

Измерялось время выполнения стадий BUILD и SWAP, без учета времени, потраченного на построение матрицы расстояний, а также измерялось число итераций алгоритма. Были проведены эксперименты для следующих значений размерности матрицы расстояний и числа процессоров:

Значения размерности: [2500, 2000, 1500, 1000, 500, 200, 150, 100, 50]
Значения числа процессоров: [500, 400, 256, 128, 64, 32, 16, 8, 4, 1]

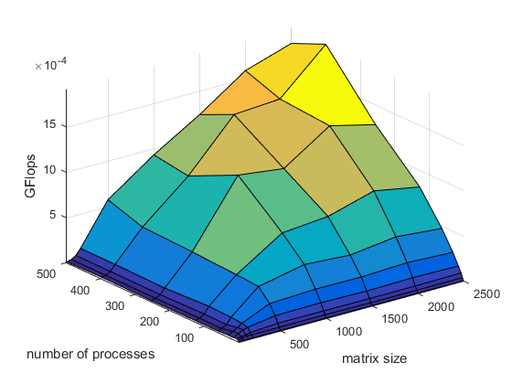
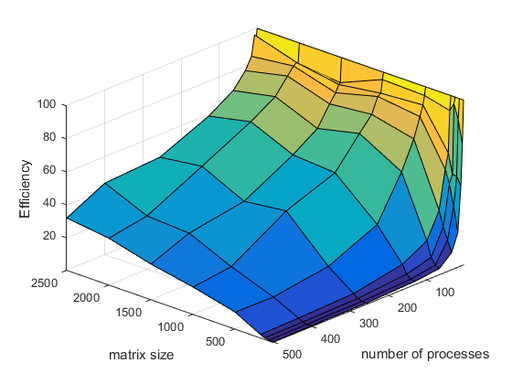
Полученные графики производительности и эффективности представлены на рисунках 4 и 5 соответственно.

Рисунок 4. Зависимость производительности реализации параллельного алгоритма от размера матрицы и числа процессоров

Рисунок 5. Зависимость эффективности реализации параллельного алгоритма от размера матрицы и числа процессоров.

Таким образом, из полученных графиков можно сделать вывод о том, что эффективность задачи при фиксированном размере входной матрицы понижается с увеличением числа процессоров, это связано с увеличением передачи данных между процессорами. При фиксированном значениии числа процессоров эффективность увеличивается при увеличении размера входной матрицы, это в свою очередь связано с тем, что доля времени, потраченного на передачу данных между процессорами, от общего затраченного на вычисления времени уменьшается.

В экспериментах была использована сторонняя реализация алгоритма, с небольшими изменениями она выложена в репозитории[1]

2.7 Существующие реализации алгоритма

1. ELKI реализует несколько вариантов алгоритма кластеризации, включая алгоритм PAM. Написан на Java
2. Java-ML. Включает реализацию k-metoid. Написан на Java
3. Julia содержит реализацию k-metoid в пакете для кластеризации JuliaStats
4. R включает различные варианты k-means в пакете flexclust. Алгоритм PAM реализован в пакете cluster
5. MATLAB. Реализованы PAM, CLARA и другие алгоритмы кластеризации
6. Python. Алгоритм PAM реализован как k-medoids в пакете pyclust, содержащем также различные варианты k-means