Участник:Error0x0/Алгоритм Ланцоша для арифметики с плавающей точкой с полной переортогонализацией

Алгоритм Ланцоша для арифметики с плавающей точкой с полной переортогонализацией
Последовательный алгоритм
Последовательная сложность	[math]O(k^2 n)[/math]
Объём входных данных	[math]n^2[/math]
Объём выходных данных	[math]n[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(k \log k \log n)[/math]
Ширина ярусно-параллельной формы	[math]O(kn)[/math]

Автор описания: В. А. Янушковский

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм Ланцоша представляет собой итерационный алгоритм для вычисления собственных значений симметрической матрицы. Идея алгоритма заключается в построении матрицы [math]Q_k = [q_1, ..., q_k][/math] из ортонормированных векторов Ланцоша и использовании собственных значений трёхдиагональной матрицы [math]T_k = Q_k^T A Q_k[/math] (чисел Ритца) как приближения к искомым собственным числам матрицы.

1.2 Математическое описание алгоритма

Пусть дана матрица [math]A[/math]. Пусть [math]q_1 = b/||b||_2, \beta_0=0, q_0=0[/math] Алгоритм производит [math]k[/math] итераций на каждой из которых:

1. вычисляется [math]z = Aq_j[/math],
2. производится переортогонализация [math]z = z - \sum^{j-1}_{i=1} {(z^T q_i)q_i}[/math],
3. [math]\beta_j = ||z||_2[/math], если [math]\beta_j = 0[/math], алгоритм останавливается,
4. [math]q_{j+1} = z/\beta_j[/math],
5. вычисляются собственные значения и векторы матрицы [math]T_j = Q_j^T A Q_j[/math].

1.3 Вычислительное ядро алгоритма

Основной вклад в сложность алгоритма даёт полная переортогонализация внутри каждой итерации:

[math]z = z - \sum^{j-1}_{i=1} {(z^T q_i)q_i}[/math]

1.4 Макроструктура алгоритма

Алгоритм имеет следующую макроструктуру:

• Начальная инициализация (деление вектора на норму [math]q_1 = b/||b||_2[/math])
• Далее [math]k[/math] итераций, каждая из которых может быть разложена:
  • Умножение матрицы на вектор ([math]z = Aq_j[/math])
  • Переортогонализация [math]z = z - \sum^{j-1}_{i=1} {(z^T q_i)q_i}[/math]
  • Нахождение следующего вектора [math]q_{j+1} = z/\beta_j[/math], где [math]\beta_j = ||z||_2[/math]
  • Нахождение следующего собственного значения и вектора матрицы [math]T_j = Q_j^T A Q_j[/math] (числа Ритца, используется метод "разделяй и властвуй")

1.5 Схема реализации последовательного алгоритма

beta[0] = 0 # инициализация
q[0] = 0
q[1] = b / norm(b) # вычисление первого столбца
for j in [1 .. k]: # k итераций
    z = mul(A, q[j]) # вектор Ланцоша как произведение матрицы A на столбец q[j]
    alpha[j] = scalar_mul(q[j], z) # вычисление alpha[j]
    for i in [1 .. j - 1]: # полная переортогонализация
        z -= scalar_mul(z, q[i]) * q[i]
    beta[j] = norm(z) # вычисление нормы z
    if beta[j] == 0: # останов, если норма z равна нулю
        break
    result.append(next_ritz_number(alpha, beta, j)) # вычисление следующего собственного значения и вектора матрицы Tj
return result

1.6 Последовательная сложность алгоритма

Основной вклад в сложность даёт полная переортогонализация: на каждой из [math]k[/math] итераций для всех [math]i \in [0...j-1][/math] выполняется [math]2n[/math] умножений и [math]2n[/math] сложений, итого [math]\frac{k(k-1)}{2} 4n \approx 2k^2 n[/math]. Таким образом, для метода с полной переортогонализацией сложность составляет [math]O(k^2 n)[/math], сложность по памяти -- [math]O(kn)[/math].

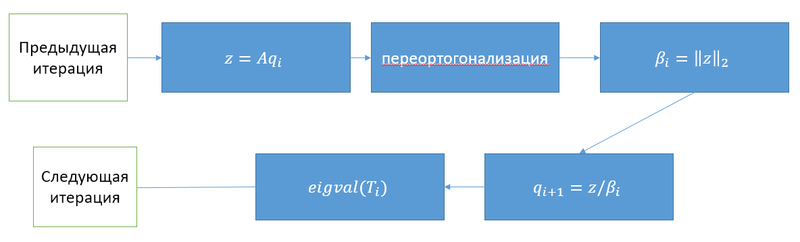
1.7 Информационный граф

На рисунке приведён информационный граф одной итерации алгоритма

Рисунок 1. Информационный граф итерации алгоритма

1.8 Ресурс параллелизма алгоритма

Для процесса переортогонализации возможна параллельная оптимизация в двух местах:

• Итерации внутреннего цикла могут вычисляться параллельно, однако, требуется суммирование вычитаемых векторов, соответственно, сложность переортогонализации можно снизить с [math]O(kn)[/math] до [math]O(n \log k)[/math]
• В каждой итерации внутреннего цикла возможно распараллеливание вычисления выражения справа (скалярное произведение и умножение вектора на число), что теоретически позволяет снизить сложность итерации с [math]O(n)[/math] до [math]O(log(n))[/math]

1.9 Входные и выходные данные алгоритма

Входные данные: квадратная симметрическая матрица [math]A[/math] порядка [math]n[/math]

Объём входных данных: [math]n^2[/math]

Выходные данные: собственные числа матрицы

Объём выходных данных: [math]n[/math]

1.10 Свойства алгоритма

Полная переортогонализация соответствует повторной процедуре ортогонализациии Грама-Шмидта для обеспечения ортогональности вектора [math]z[/math] векторам [math]q_1, ..., q_k[/math]. В случае идеально точной арифметики данная переортогонализация не требовалась бы, однако в реальных вычислениях ошибки округления приводят к потере ортогональности, в связи с чем требуется переортогонализация. Однако, единственной проблемой, возникающей при отсутствии переортогонализации, является появление повторных копий чисел Ритца (собственных значений), что в случае, если не требуется установление кратностей собственных значений, допустимо.

Вычислительная мощность алгоритма примерно равна [math]2k^2 / n[/math].

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Исследование масштабируемости алгоритма проводилось на суперкомпьютере IBM Blue Gene/P ВМК МГУ.

Алгоритм тестировался на следующих параметрах:

• размер входной матрицы: 2048-8192 с шагом 512
• число узлов: 1-256

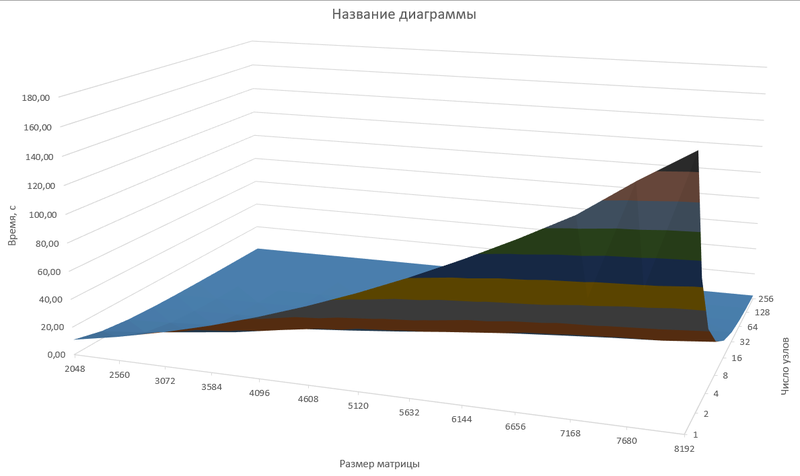
Зависимость времени выполнения от параметров изображена на графике:

Из рисунка видно, что алгоритм хорошо масштабируется, время выполнения на одном ядре растёт существенно быстрее чем на множестве ядер. При этом, для маленькой матрице на большом числе ядер прирост эффективности практически отсутствует.

Используемая реализация алгоритма на языке C++

Пример компиляции и запуска:

 $ mpixlcxx_r -o lanczos lanczos.cpp
 $ mpisubmit.bg -n 256 -w 00:5:00 lanczos

2.7 Существующие реализации алгоритма

Библиотека NAG Library содержит ряд процедур для решения СЛАУ и поиска собственных значений на основе алгоритма Ланцоша.

MATLAB и GNU Octave позволяют с помощью функции eigs() находить собственные значения на основе данного алгоритма.

Matlab-реализация доступна как часть Gaussian Belief Propagation Matlab Package. GraphLab содержит несколько параллельных реализаций алгоритма на C++.