Эта работа успешно выполнена
Преподавателю: в основное пространство, в подстраницу
Данное задание было проверено и зачтено.
Проверено Frolov и VadimVV.

Нахождение собственных чисел квадратной матрицы методом QR-разложения
Последовательный алгоритм
Последовательная сложность	[math]O(n^3 + N \times n^2)[/math]
Объём входных данных	[math]n^2[/math]
Объём выходных данных	[math]n[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]N \times O(n)[/math]
Ширина ярусно-параллельной формы	[math]O(n^2)[/math]

Основные авторы описания: Ф. В. Морозов, Н. Ф. Пащенко

Описание составлено совместно, точно выделить вклад отдельных авторов невозможно.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Для решения ряда задач механики, физики, химии требуется получение всех собственных значений (собственных чисел), а иногда и всех собственных векторов некоторых матриц. Эту задачу называют полной проблемой собственных значений^[1]. Если рассматриваются матрицы общего вида, порядок которых не больше тысячи (нескольких тысяч), то для вычисления всех собственных значений (и собственных векторов) можно рекомендовать QR-алгоритм. Он был разработан в начале 1960-х годов независимо В. Н. Кублановской (Россия) и Дж. Фрэнсисом (Великобритания)^[2].

Нахождение собственных чисел матрицы [math]A[/math] методом QR-разложения (QR-алгоритм) заключается в построении последовательности матриц, сходящейся по форме к клеточному правому треугольному виду. Матрицы [math]A_k[/math] данной последовательности строятся с использованием QR-разложения таким образом, что они подобны между собой и подобны исходной матрице [math]A[/math], поэтому их собственные значения равны. Характеристический многочлен клеточной правой треугольной матрицы равен произведению характеристических многочленов ее диагональных клеток^[1]. Его корни — собственные значения матрицы, которые согласно вышесказанному и являются искомыми.

1.2 Математическое описание алгоритма

Известно, что произвольная квадратная матрица может быть представлена в виде произведения унитарной (в вещественном случае ортогональной) и верхней треугольной матриц. Такое разложение называется QR-разложением.

1.2.1 QR-алгоритм

Пусть [math]A_0 = A[/math] — исходная матрица. Для [math]k = 1, 2, \ldots[/math]:

[math]A_{k-1} = Q_kR_k[/math], где [math]Q_k[/math] — унитарная (ортогональная) матрица, [math]R_k[/math] — верхняя треугольная матрица;
[math]A_k = R_kQ_k[/math].

Заметим, что [math]A_k = R_kQ_k = Q_k^{-1}A_{k-1}Q_k[/math], то есть матрицы [math]A_k[/math] и [math]A_{k-1}[/math] подобны для любого [math]k[/math]. Таким образом, матрицы [math]A_1, A_2, \ldots[/math] подобны исходной матрице [math]A[/math] и имеют те же собственные значения. При выполнении некоторых условий последовательность [math]\{A_k\}[/math] сходится к верхней треугольной матрице [math]\hat{A}[/math], на диагонали которой расположены искомые собственные значения.

1.2.2 Сходимость QR-алгоритма

Сходимость QR-алгоритма трактуется как сходимость к нулю поддиагонального блока матрицы [math]A_k[/math].

Предположим, что для матрицы [math]A \in \mathbb{C}^{n \times n}[/math] выполнены следующие условия:

[math]A = X \Lambda X^{-1}, \quad \Lambda = \begin{bmatrix} \Lambda_1 & 0 \\ 0 & \Lambda_2 \end{bmatrix}, \quad \Lambda_1 \in \mathbb{C}^{m \times m}, \quad \Lambda_2 \in \mathbb{C}^{r \times r}[/math];
[math]\left | \lambda_1 \right | \ge \ldots \ge \left | \lambda_m \right | \gt \left | \lambda_{m+1} \right | \ge \ldots \ge \left | \lambda_{m+r} \right | \gt 0, \quad \{ \lambda_1, \ldots, \lambda_m \} = \lambda(\Lambda_1), \quad \{ \lambda_{m+1}, \ldots, \lambda_{m+r} \} = \lambda(\Lambda_2)[/math];
ведущая подматрица порядка [math]m[/math] в [math]X^{-1}[/math] невырожденная.

И пусть QR-алгоритм порождает последовательность матриц

[math]A_k = \begin{bmatrix}A_{11}^{(k)} & A_{12}^{(k)} \\ A_{21}^{(k)} & A_{22}^{(k)}\end{bmatrix}[/math].

Тогда [math]A_{21}^{(k)} \rightarrow O[/math] при [math] k \rightarrow \infty[/math].

Если блок [math]A_{21}^{(k)}[/math] достаточно мал, то он заменяется нулевым, и собственные значения ищутся для диагональных блоков [math]A_{11}^{(k)}[/math] и [math]A_{22}^{(k)}[/math].

Если условия 1-3 выполнены для всех [math]1 \le m \le n - 1[/math], то к нулю сходятся все поддиагональные блоки. А это значит, что все поддиагональные элементы матриц [math]A_k[/math] стремятся к нулю, и диагональные элементы матриц [math]A_k[/math] сходятся к искомым собственным значениям матрицы [math]A[/math]^[2].

1.2.3 Сокращение затрат на одну итерацию

Одна QR-итерация для матрицы общего вида требует [math]O(n^3)[/math] арифметических операций. Это очень большие затраты, даже если итераций не очень много (обычно их требуется не больше 5 на каждое собственное значение). Для решения данной проблемы используют тот факт, что с помощью отражений или вращений матрицу [math]A[/math] можно привести к унитарно подобной верхней хессенберговой (почти треугольной) матрице:

[math]H = (h_{ij}), \quad h_{ij} = 0[/math] при [math]i \gt j + 1[/math];
[math]H = PAP^*[/math], где [math]P[/math] — произведение конечного числа отражений (или вращений).

Затем QR-алгоритм применяется к матрице [math]A_0 = H[/math].

Приведение к хессенберговой форме требует [math]O(n^3)[/math] операций, но после него любая QR-итерация будет выполняться за [math]O(n^2)[/math] операций. Сокращение затрат на одну итерацию объясняется инвариантностью хессенберговой формы по отношению к QR-итерациям^[2].

1.2.4 Уменьшение числа итераций

Скорость сходимости алгоритма зависит от отношения модулей собственных значений: чем больше отношение [math]|\lambda_{m+1}| / |\lambda_m|[/math], тем медленнее убывает поддиагональный [math](n-m) \times m [/math] блок. Для увеличения скорости сходимости алгоритма можно перейти от матрицы [math]A[/math] к матрице [math](A - sI)[/math], где [math]s \in \mathbb{C}[/math], а [math]I[/math] — единичная матрица, в надежде, что [math]|\lambda_{m+1} - s| / |\lambda_m - s| \ll |\lambda_{m+1}| / |\lambda_m|[/math].

Такой подход называется QR-алгоритмом со сдвигами и имеет следуюший вид:

[math]A_0 = A[/math] — исходная матрица. Для [math]k = 1, 2, \ldots[/math]:

[math]A_{k-1} - s_kI= Q_kR_k[/math] (QR-разложение);
[math]A_k = R_kQ_k + s_kI[/math].

QR-алгоритм со сдвигами является частным случаем обобщенного QR-алгоритма (QR-алгоритма с мультисдвигами), в котором на каждой итерации используется полином [math]f_k[/math]:

[math]f_k(A_{k-1}) = Q_kR_k[/math];
[math]A_k = Q_k^{-1}A_{k-1}Q_k[/math].

1.3 Вычислительное ядро алгоритма

Основное время работы алгоритма приходится на вычисление QR-разложения на итерациях алгоритма.

Для получения QR-разложения могут использоваться метод Хаусхолдера, метод Гивенса или процесс ортогонализации Грама-Шмидта.

При использовании хессенберговой формы приведение к ней имеет сложность, сравнимую с последующими итерациями QR-алгоритма.

1.4 Макроструктура алгоритма

Основные элементы алгоритма:

(опционально) приведение к хессенберговой форме;
QR-разложение;
умножение плотных матриц.

1.5 Схема реализации последовательного алгоритма

Пример реализации на языке Python:

def get_eigenvalues(A, use_hessenberg_form):
    """Вычисление собственных значений матрицы методом QR-разложения

    Параметры:
    A -- квадратная матрица
    use_hessenberg_form -- использовать ли приведение к хессенберговой форме
    """
    if use_hessenberg_form:
        A = to_hessenberg_form(A) #Матрица приводится к хессенберговой форме
    while not is_upper_triangular(A): #Является ли матрица верхней треугольной
        Q, R = QR_decomposition(A) #Производится QR-разложение матрицы
        A = R * Q
    #Собственными значениями являются диагональные элементы полученной матрицы
    return diagonal_items(A)

1.6 Последовательная сложность алгоритма

Рассмотрим сложность отдельных элементов алгоритма:

QR-разложение имеет сложность [math]O(n^3)[/math] арифметических операций;
сложность перемножения квадратных матриц равна [math]n^3 + O(n^2)[/math];
для проверки, является ли матрица верхней треугольной, необходимо [math]O(n^2)[/math] операций.

Таким образом, каждая итерация имеет кубическую сложность и, если алгоритм сходится через [math]N[/math] итераций, общая сложность составит [math]N \times O(n^3)[/math] арифметических операций.

Сложность построения хессенберговой формы составляет [math]O(n^3)[/math], одна итерация алгоритма для хессенберговой матрицы имеет сложность [math]O(n^2)[/math]. Общая сложность QR-алгоритма с предварительным приведением матрицы к хессенберговой форме равна [math]O(n^3 + N \times n^2)[/math] арифметических операций, где [math]N[/math] — число итераций алгоритма.

1.7 Информационный граф

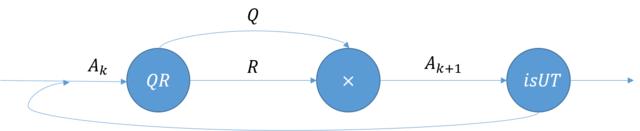
Рисунок 1. Информационный граф.

Узлы графа:

[math]QR[/math] — QR-разложение;
[math]\times[/math] — перемножение матриц;
[math]isUT[/math] — проверка, является ли матрица верхней треугольной.

1.8 Ресурс параллелизма алгоритма

Несмотря на то что QR-алгоритм является последовательным, действия, выполняемые на каждой итерации, могут быть эффективно выполнены параллельно:

параллельная сложность QR-разложения составляет [math]O(n)[/math] при использовании метода Гивенса или [math]O(n^2)[/math] при использовании метода Хаусхолдера;
параллельная сложность умножения матриц равна [math]O(n)[/math];
для проверки, является ли матрица верхней треугольной, достаточно одного яруса.

Таким образом, при классификации по высоте ярусно-параллельной формы сложность равна [math]N \times O(n)[/math] или [math]N \times O(n^2)[/math] в зависимости от используемого метода QR-разложения.

При классификации по ширине ярусно-параллельной формы, сложность QR-алгоритма составляет [math]O(n^2)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные: плотная квадратная матрица [math]A[/math] порядка [math]n[/math].

Объем входных данных: [math]n^2[/math].

Выходные данные: собственные числа матрицы [math]A[/math].

Объем выходных данных: [math]n[/math].

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности является квадратичным или линейным в зависимости от метода QR-разложения.
Вычислительная мощность алгоритма равна [math]N \times O(n)[/math].
Число итераций [math]N[/math] заранее неизвестно, то есть алгоритм недетерминирован.
Если рассмотренные в разделе «Сходимость QR-алгоритма» условия 1-3 не выполнены, то, возможно, ни один из поддиагональных блоков не сходится к нулю. Это означает, что в общем случае QR-алгоритм не обязан сходиться. Однако внеся в элементы матрицы сколь угодно малые возмущения, всегда можно удовлетворить указанным условиям.
Скорость сходимости алгоритма зависит от отношения собственных значений, чем ближе по модулю собственные значения, тем медленее скорость сходимости.
Если матрица [math]A[/math] эрмитова, то хессенбергова матрица [math]H[/math] будет трехдиагональной, и сложность одной QR-итерации составит [math]O(n)[/math] операций.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

Исследование проводилось на узлах раздела test суперкомпьютера "Ломоносов"^[3] Суперкомпьютерного комплекса Московского университета.

Исследовалась реализация QR-алгоритма из библиотеки Intel MKL версии 11.2.0 (функции LAPACKE_sgehrd и LAPACKE_shseqr). Была написана программа на языке C, использовался компилятор Intel C++. Пример компиляции программы и запуска для матрицы размера [math]8000 \times 8000[/math]:

 $ mpicc qr.c -o _scratch/qr -L${MKLROOT}/lib/intel64 -lmkl_rt -lpthread -lm -ldl
 $ sbatch -n 1 -p test run _scratch/qr 8000

Оценивалось время вычисления собственных чисел произвольной квадратной матрицы для различных значений порядка матрицы (Matrix size) и числа потоков (Threads). Ввиду того, что количество операций зависит от числа итераций алгоритма, оценить производительность не удается.

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

число потоков [1 : 8];
размер матрицы [2000 : 8000] с шагом 500.

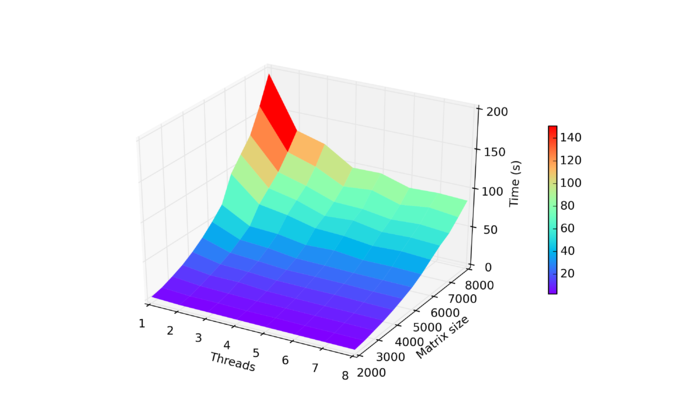
На рисунке приведен график времени работы выбранной реализации QR-алгоритма в зависимости от изменяемых параметров запуска.

Рисунок 2. Производительность QR-алгоритма.

Из рисунка видно, что алгоритм хорошо масштабируется. Время выполнения в зависимости от размера задачи растет значительно быстрее при использовании одного потока по сравнению с использованиемм нескольких потоков. Увеличение числа потоков при фиксированном размере задачи приводит к уменьшению времени выполнения. Для матрицы размера [math]8000 \times 8000[/math] время работы однопоточной реализации более чем в два раза превосходит время работы параллельной.

Исходный код программы на языке C и скрипт для обработки результатов доступны на github.

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

LAPACK (Fortran, C). Имеется реализация в Intel MKL:
- ?geev - нахождение собственных значений матрицы;
- ?gehrd - приведение к хессенберговой форме;
- ?hseqr - нахождение собственных значений матрицы в хессенберговой форме.
ScaLAPACK (Fortran, C). Имеется реализация в Intel MKL:
- p?gehrd- приведение к хессенберговой форме;
- p?hseqr - нахождение собственных значений матрицы в хессенберговой форме.
numpy.linalg.eigvals (Python) - использует ?geev из LAPACK.
Eigen (C++).
IBM ESSL (Fortran, C, C++).

3 Литература

↑ ^1,0 ^1,1 Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. Численные методы. — 6-е изд. — М.: БИНОМ. Лаборатория знаний, 2008. — 636 с.
↑ ^2,0 ^2,1 ^2,2 Тыртышников Е. Е. Методы численного анализа. — М.: Академия, 2007. — 320 c.
↑ Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, N 7, С. 36-39.

[.D0.91.D0.B0.D1.85.D0.B2.D0.B0.D0.BB.D0.BE.D0.B2-1] 1,0 ^1,1 Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. Численные методы. — 6-е изд. — М.: БИНОМ. Лаборатория знаний, 2008. — 636 с.

[.D0.A2.D1.8B.D1.80.D1.82.D1.8B.D1.88.D0.BD.D0.B8.D0.BA.D0.BE.D0.B2-2] 2,0 ^2,1 ^2,2 Тыртышников Е. Е. Методы численного анализа. — М.: Академия, 2007. — 320 c.

[Lomonosov-3] Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, N 7, С. 36-39.

[1]

[2]

[3]

Участник:F-morozov/Нахождение собственных чисел квадратной матрицы методом QR разложения (4)