Участник:Greno4ka/Вычисление определенного интеграла с использованием адаптивно сгущающейся сетки

Авторы: Устинов Г.А.(п. 1.6-1.10, 2.4, 2.7) Лиджиев Д.В.(п. 1.1-1.6)

Вычисление определенного интеграла с использованием адаптивно сгущающейся сетки
Последовательный алгоритм
Объём входных данных	[math]O(1)[/math]
Объём выходных данных	[math]O(1)[/math]

1 ЧАСТЬ. Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Вычисление определенного интеграла с использованием адаптивно сгущающейся сетки примечательно тем, что на разных участках интервала интегрирования количество узлов сетки зависит от необходимой точности. Вычисление на равномерной сетке неэффективно, поскольку предполагает равномерное сгущение сетки на всем отрезке интегрирования, без учета характера изменения подынтегральной функции.
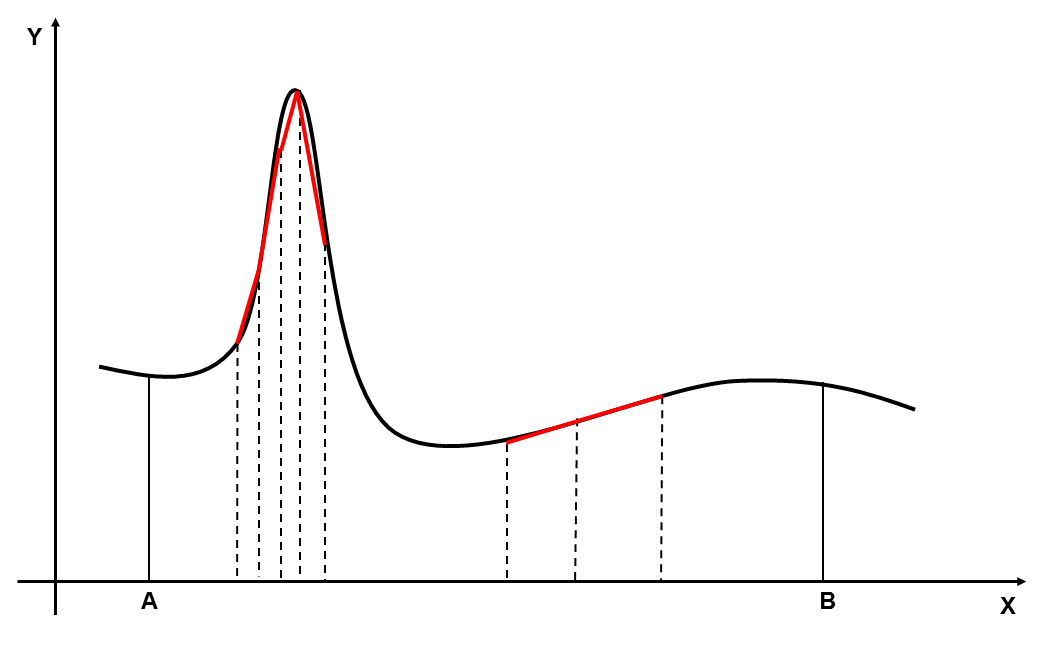
В данном алгоритме используется адаптивное разбиение участка интегрирования: размер конкретного отрезка определяется во время подсчета значения функции на нем самом. Если заданная точность не была достигнута на данном отрезке, он рекурсивно разбивается на несколько новых и функция подсчитывается уже на них. Таким образом, выигрыш от применения рассмотренного алгоритма рекурсивного разбиения достигается за счет возможности использования сеток с разным числом узлов на разных участках интервала интегрирования. Как правило это бывает очень полезно при расчёте интегралов функций, содержащих области с высокими градиентами.

1.2 Математическое описание алгоритма

В качестве модельной задачи рассматривается проблема вычисления с точностью ε значение определенного интеграла:

[math]I(a,b) = \int_a^b{f(x)dx}[/math]

Пусть на отрезке [math] [a,b] [/math] задана равномерная сетка, содержащая [math] n+1 [/math] узел:

[math] x_{i} = a + \frac{(b - a)} {n} i, i = 0,...,n [/math]

Тогда, согласно методу трапеций, можно численно найти определенный интеграл от функции [math] f (x) [/math] на отрезке [math][a,b][/math]:

[math] \int_a^b{f(x)dx} = \frac{b - a}{n} \left( \frac{f(x_0)}{2} + \sum^{n-1}_{i=1} {f(x_i)} + \frac{f(x_n)}{2} \right)[/math]

Будем полагать значение I найденным с точностью ε, если выполнено условие

[math] |I_{n_1} - I_{n_2}| \leq \epsilon |I_{n_2}|, n_1 \gt n_2, [/math] где [math] n_1 [/math] и [math] n_2 [/math] - количество узлов, образующих две разные сетки.

Данный метод неэффективен, так как на всём интервале интегрирования используется равномерная сетка, тогда как число точек, необходимых для достижения заданной точности, зависит от вида функции и может сильно различаться на разных участках сегмента интегрирования.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма состоит из основного цикла алгоритма и сложность зависит от количества проходов по нему. То есть основное время работы алгоритма приходится на следующие операции:
- нахождение середины отрезка и значения функции в этой точке;
- вычисление частичных сумм на половинах отрезка;
- работа со стеком.

1.4 Макроструктура алгоритма

Алгоритм итерационный. Сначала значение текущего отрезка равно общему отрезку интегрирования. На каждой итерации выполняются следующие действия:
- На текущем отрезке считается приближенное значение интеграла
- Текущий отрезок делится пополам, и на получившихся отрезках высчитываются интегралы
- Сравнивается интеграл на всём отрезке с суммой двух интегралов на половинах. Если достигнута заданная точность, то:

1. Добавить значение интеграла текущего отрезка к общему интегралу
   
2. Если стек пуст, то завершить алгоритм
   
3. Иначе достать из стека отрезок и присвоить его значение текущему отрезку.
   

- Иначе

1. Одну половину отрезка положить в стек
   
2. Текущему отрезку присвоить значение второй половины
   

1.5 Схема реализации последовательного алгоритма

struct SumRecord {
	double A;
	double fA;
	double B;
	double fB;
	double s;
};

double f(double x)
{
	return (1/x*x)*sin(1/(x*x))*sin(1/(x*x));
}

const double eps = 0.00001;

double JLS(double A, double B) {
	stack<SumRecord> localStack;
	SumRecord tmpRecordAB;

	double J = 0;
	double fA = f(A);
	double fB = f(B);
	double sAB = (fA + fB) * (B - A) / 2.;
	while (1) {
		double C = (A + B) / 2.;

		double fC = f(C);
		double sAC = (fA + fC) * (C - A) / 2.;
		double sCB = (fC + fB) * (B - C) / 2.;
		double sACB = sAC + sCB;
		if (abs(sAB - sACB) >= eps * abs(sACB)) {
			SumRecord tmpRecordAC = { A, fA, C, fC, sAC };
			localStack.push(tmpRecordAC);
			A = C;
			fA=fC;
			sAB = sCB;
		} else {
			J += sACB;
			if (localStack.empty())
				break;
			else {
				tmpRecordAB = localStack.top();
				A = tmpRecordAB.A;
				fA = tmpRecordAB.fA;
				B = tmpRecordAB.B;
				fB = tmpRecordAB.fB;
				sAB = tmpRecordAB.s;
				localStack.pop();
			}
		}
	}
	return J;
}

Функция получает координаты начала и конца отрезка. В цикле проверяется условие if (|sAB - sACB| ≥ ε|sACB|). Если оно соблюдается, то один отрезок помещается в стек, а на другом продолжаются вычисления до тех пор, пока не достигается необходимая точность. Затем вычисляется интеграл на отрезках, концы которых берутся из стека.

1.6 Последовательная сложность алгоритма

Оценить аналитически последовательную сложность представленного алгоритма невозможно, поскольку нельзя указать количество разбиений отрезка интегрирования для каждой отдельно взятой функции, оно зависит от свойств конкретно взятой функции.

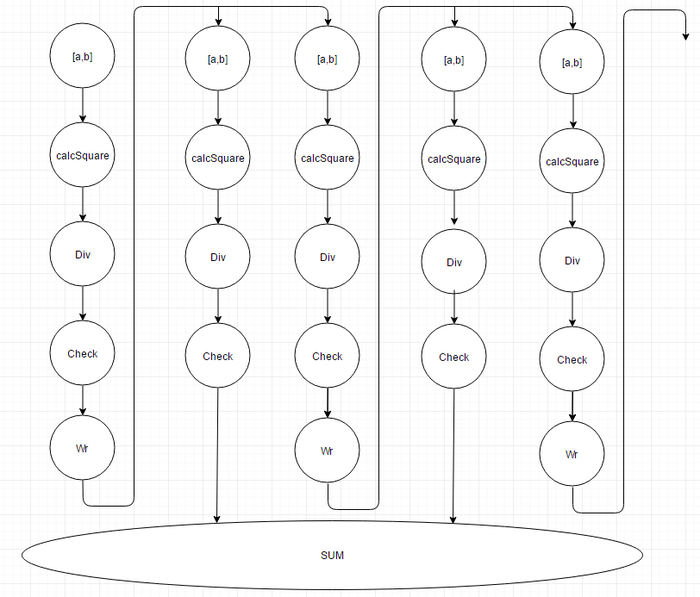
1.7 Информационный граф

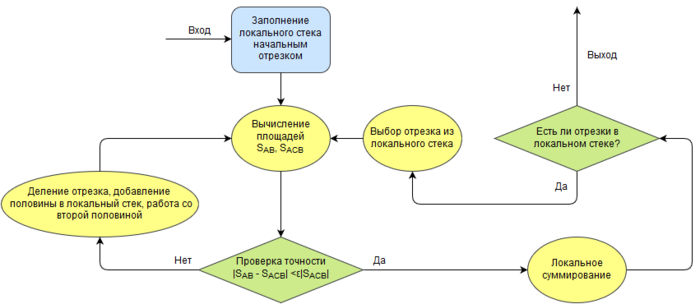
В последовательной версии алгоритма используется только локальный стек, в который помещаются отрезки, перед очередным этапом деления отрезка. Таким алгоритм чем-то похож на алгоритм рекурсивного деления, только без прямого использования рекурсии. Отрезок делится до тех пор, пока не будет достигнута необходимая точность, вторая половина отрезка будет помещаться в локальный стек на каждом этапе деления. После достижения нужной точности, первым будет исследован последний добавленный отрезок, то есть соответствующий второй половине отрезка, разделённого на предыдущем этапе. Следующий рисунок содержит блок-схему данного алгоритма.

Рис.1.

В параллельной версии алгоритма, появляется дополнительный глобальный стек, в который будут помещаться отрезки из локальных стеков параллельных процессов, и доступ к которому имеют все процессы. Он находится в общей памяти и содержит границы отрезков. Процессы обмениваются с ним данными, распределяя таким образом отрезки между собой. Когда в локальном стеке заканчиваются элементы, процесс обращается к глобальному стеку, чтобы получить их.
Изначально в глобальный стек помещается один отрезок, соответствующий участку интегрирования. Существуют реализации, где локальные стеки полностью отсутствуют, а все отрезки хранятся в глобальном стеке. Такой вариант проще реализовать, но его недостаток в том, что увеличивается количество обращений процессов к глобальному стеку, и каждый процесс должен ждать своей очереди, что может привести к увеличению времени работы программы.

Рис.2. Информационный граф для алгоритма глобального стека. [a,b] - выбор отрезка, calcSquare - вычисление площади, Div - деление отрезка пополам, Check - проверка достижения точности, Wr - запись отрезка в локальный/глобальный стек, Sum - общая сумма

1.8 Ресурс параллелизма алгоритма

Так как сложность алгоритма существенно зависит от свойств входной функции, оценить ресурс параллелизма не представляется возможным. Рекурсивное деление областей интегрирования и поиск на них частичных сумм зависит непосредственно от конкретной функции и ее свойств.

1.9 Входные и выходные данные алгоритма

Входные данные:

• функция [math]y = f(x)[/math];
• точность [math]\epsilon[/math];
• границы отрезка интегрирования [math]a[/math], [math]b[/math].

Выходные данные:

• число [math]I[/math], равное [math]\int_a^b{f(x)dx}[/math] с точностью [math]\epsilon[/math].

1.10 Свойства алгоритма

1. Алгоритм адаптируется под конкретные особенности заданной функции.
2. В параллельной версии алгоритма на основе не требуется управляющий процесс. Распределение отрезков и финальное сложение можно провести на нулевом процессе.
3. Алгоритм является детерминированным, поскольку при одинаковых входных данных получается одинаковый результат.

2 ЧАСТЬ. Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Вариант реализации параллельного алгоритма представлен ниже.

sem_t semGlobalSum, semGlobalStack, semTaskPresent;

int numberOfActiveProcs = 0;
unsigned int maxGSelements = 10, maxLSelements = 5;
double integral = 0;
stack<SumRecord> globalStack;

void *JLS_thr(void *processNumber) {
	stack<SumRecord> localStack;
	double J = 0;
	int pN = *((int*)(&processNumber));
	
	while (1) {
		sem_wait(&semTaskPresent);
		sem_wait(&semGlobalStack);

		SumRecord tmpRecordAB = globalStack.top();
		double A = tmpRecordAB.A;
		double fA = tmpRecordAB.fA;
		double B = tmpRecordAB.B;
		double fB = tmpRecordAB.fB;	
		double sAB = tmpRecordAB.s;
		globalStack.pop();

		if (!globalStack.empty())
			sem_post(&semTaskPresent);
		if (A <= B)
			numberOfActiveProcs++;
			sem_post(&semGlobalStack);
		if (A > B) break;		

		while (1) {
			double C = (A + B) / 2;
			double fC = f(C);
			double sAC = (fA + fC) * (C - A) / 2;
			double sCB = (fC + fB) * (B - C) / 2;
			double sACB = sAC + sCB;
			if (abs(sAB - sACB) < eps * abs(sACB)) {
				J += sACB;
	
				if (localStack.empty())
					break;
				else {
					tmpRecordAB = localStack.top();
					A = tmpRecordAB.A;
					fA = tmpRecordAB.fA;
					B = tmpRecordAB.B;
					fB = tmpRecordAB.fB;
					sAB = tmpRecordAB.s;
					localStack.pop();
				}
			} else {
				SumRecord tmpRecordAC = { A, fA, C, fC, sAC };
				localStack.push(tmpRecordAC);
				A = C;
				fA=fC;
				sAB = sCB;
			}

			if ((localStack.size() > maxLSelements) && 
				(globalStack.empty())) {
				sem_wait(&semGlobalStack);
				if (globalStack.empty()) {
					sem_post(&semTaskPresent);
				}
				while ((localStack.size() > 1)
						&& (globalStack.size() < maxGSelements)) {
					SumRecord tmpRecord = localStack.top();
					localStack.pop();
					globalStack.push(tmpRecord);
				}
				sem_post(&semGlobalStack);
			}
		}

		sem_wait(&semGlobalStack);
		numberOfActiveProcs--;
		if ((!numberOfActiveProcs) && (globalStack.empty())) {
			for (int i = 0; i < nproc; i++) {
				SumRecord terminalRecord = { 2, 1, 0 };
				globalStack.push(terminalRecord);
			}
			sem_post(&semTaskPresent);
		}
		sem_post(&semGlobalStack);
	}

	sem_wait(&semGlobalSum);
	integral += J;
	sem_post(&semGlobalSum);
	return 0;
}

pthread_t *thread;

typedef void *ThrSub(void *);

void StartThrTask(int NumberOfProcs, ThrSub *thrFunc) {
	thread = (pthread_t *) malloc(NumberOfProcs * sizeof(pthread_t));

	for (int i = 0; i < NumberOfProcs; i++)
		pthread_create(&(thread[i]), NULL, thrFunc, (void *) i);
#ifdef HAVE_THR_SETCONCURRENCY_PROTO
	int thr_setconcurrency(int);
	thr_setconcurrency(NumberOfProcs);
#endif 
}

void WaitThrTask(int NumberOfProcs) {
	for (int i = 0; i < NumberOfProcs; i++)
		pthread_join(thread[i], NULL);
}

int main() {
	double A = 10e-5, B = 1;

	sem_init(&semGlobalSum, 0, 1);
	sem_init(&semGlobalStack, 0, 1);
	sem_init(&semTaskPresent, 0, 0);
	double fA = f(A);
	double fB = f(B);
	SumRecord tmpRecordAB = { A, fA, B, fB, (fA + fB) * (B - A) / 2. };
	globalStack.push(tmpRecordAB);
	sem_post(&semTaskPresent);
	StartThrTask(nproc, JLS_thr);
	WaitThrTask(nproc);
	return 0;
}

2.7 Существующие реализации алгоритма

Существует реализация в библиотеке ALGLIB
Есть реализация с использованием OpenMP от университета RWTH AACHEN UNIVERSITY
Кроме того, схема реализации алгоритма представлена Якобовским М. В.