Участник:Hromovalexander/Алгоритм динамической иерархической кластеризации CHAMELEON

Эта работа прошла предварительную проверку Дата последней правки страницы: 06.02.2017 Данная работа соответствует формальным критериям. Проверено ASA.

Автор статьи: Хромов А. К.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм CHAMELEON - алгоритм динамической иерархической кластеризации графа. Кластеризация - разбиение графа на несколько подграфов таким образом, чтобы объекты внутри одного кластера были максимально близки (схожи), а данные двух различных кластеров максимально различались. Различие и схожесть объектов определяются некоей метрикой, известной заранее. Количество кластеров, на которые будет разбит граф, заранее неизвестно, и зависит от свойств объекта и выбранной метрики. Простейшей возможной метриков является расстояние между точками (если предполагать, что у каждой вершины графа есть координаты).

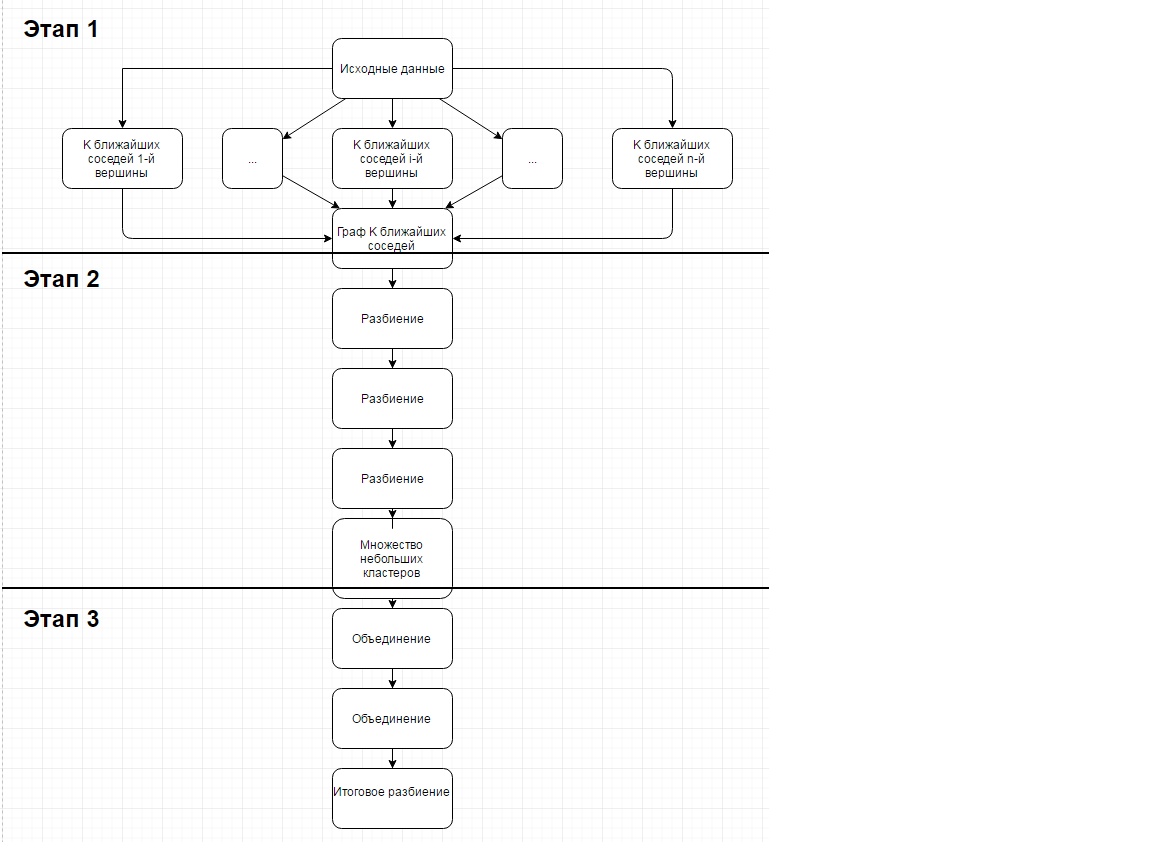
Алгоритм состоит из 3-х основных этапов:

1-й этап заключается в построении изначального графа по множеству объектов и метрике схожести по принципу k ближайших соседей (вершина графа, соответствующая некому объекту соединяется с k вершинами, расстояние до которых минимально)

2-й этап заключается в разбиении построенного графа на небольшие кластеры (связные подграфы)

3-й этап состоит в формировании итогового множества кластеров

1.2 Математическое описание алгоритма

Исходные данные

Множество из n объектов и заданные расстояния между объектами. Эта информация позволяет построить матрицу смежности, в которой будут указаны расстояния между соответствующими объектами по некой метрике. Матрица смежности симметрична, на главной диагонали стоят 0, поэтому достаточно хранить [math]\frac{n(n-1)}{2}[/math] элементов. Кроме того задаются параметры, влияющие на работу алгоритма - число k, по которому на первом этапе строится граф по принципу k ближайших соседей, и два параметра [math]{T_{ri}}[/math] и [math]{T_{rc}}[/math], используемые на третьем этапе для того, что определить, что не нужно далее продолжать кластеризацию.

Первый этап

На первом этапе строится граф [math]G(V,E)[/math], [math]V[/math] - множество вершин, [math]E[/math] - множество ребер, по принципу k ближайших соседей. Изначально граф состоит из множества вершин и пустого множества ребер. Для каждой вершины графа мы выбираем k других вершин, расстояния до которых минимальны (то есть k первых вершин в списке вершин графа, упорядоченных по увеличению расстояния до данной) и добавляем в множество ребер соответствующие ребра, соединяющие данную вершину с каждой из выбранных k вершин.

Второй этап

Состоит в итеративном разбиении графа на множество подграфов. Изначально (на первой итерации) разбиение состоит из единственного подграфа. Пусть [math]T[/math] - множество подграфов на текущей итерации. Каждая итерация выполняется следующим образом - выбирается максимальный подграф из имеющихся в разбиении по числу вершин (то есть такой подграф [math]G_1(V_1,E_1)\in{T}: \forall {G_2(V_2,E_2)\in{T}: G_2\neq G_1} =\gt |(V_1)|\gt |(V_2)|[/math] ). Выбранный подграф разбивается на 2 подграфа следующим образом - сначала выбираются все разбиения [math]G_2(V_2,E_2)[/math] и [math]G_3(V_3,E_3)[/math], такие, что [math]\min(|V_2|,|V_3|)\geq\frac{|V_1|}{4}[/math]. Далее среди всех таких разбиений выбирается такое, для которого величина [math]\sum{|E_1^*|},E_1^* [/math]- некое ребро, ведущее из вершины, попавшей в [math]G_2[/math] в вершину, попавшую в [math]G_3[/math]. В определенный момент, когда размер наибольшего кластера [math]|V_b|\leq{q*|V|}[/math], где [math]|V|[/math] - количество вершин в изначальном графе, а [math]q[/math] - предварительно заданный параметр, процесс дальнейшего разибения прекращается и алгоритм переходи на 3-й этап

Третий этап алгоритма: 

Введем несколько определений:

Абсолютной взаимной связностью пары кластеров называется величина [math]EC_{({C_i},{C_j})}[/math], вычисляется как сумма весов ребер, соединяющих вершина 1-го кластера [math]C_i[/math] с вершинами второго кластера [math]C_j[/math]. Внутренняя связность кластера [math]E_{C_i}[/math]вычисляется как сумма весов ребер, входящих в разделитель, разбивающих [math]C_i[/math] на 2 равных подграфа.

Относительная взаимная связность пары кластеров [math]RI_{(C_i,C_j)}[/math] вычисляется по формуле [math]RI_{(C_i,C_j)}=\frac{2*|EC_{(C_i,C_j)}|}{|EC_{C_i}|+|EC_{C_j}|}[/math]

Абсолютное взаимное сходство пары кластеров [math]S_{E_{(C_i,C_j)}}[/math]вычисляется как среднее сходство между связанными вершинами [math]C_i[/math] и [math]C_j[/math]

Относительное взаимное сходство пары кластеров [math]C_i[/math] и [math]C_j[/math] обозначается [math]RC_{(C_i,C_j)}[/math]и рассчитывается по формуле

[math]RC_{(C_i,C_j)}=\frac{S_{EC_{(C_i,C_j)}}}{\frac{|C_i|}{|C_i|+|C_j|}*S_{EC_{(C_i)}}+{\frac{|C_j|}{|C_i|+|C_j|}*S_{EC_{(C_j)}}}}[/math]

На третьем этапе происходит агломеративная иерархическая кластеризация.

Есть два различных подхода анализа сходства.

Первый - для каждой пары кластеров проверяется истинность следующих высказываний

[math]RI(Ci,Cj)\geq{T_{RI}} [/math] и [math]RC_{(C_{i},C_{j})}\geq{T_{RC}}[/math]

В случае, если для некоторого [math]C_i[/math] существует несколько кластеров [math]C_j[/math], удовлетворяющих этим условиям, выбирается такой [math]C_j[/math], что

значение [math]EC_{(C_i,C_j)}[/math] максимально.

Процесс останавливается, когда нет кластеров, удовлетворяющих указанным условиям (либо когда остался только 1 кластер)

Второй подход - выбирается такая пара кластеров, что [math]RI_{(C_i,C_j)}*RC^\alpha_{(C_i,C_j)}[/math] максимально, где [math]\alpha[/math] - заданный заранее параметр.

Процесс останавливается, когда нет кластеров, удовлетворяющих указанным условиям (либо когда остался только 1 кластер)

1.3  Вычислительное ядро алгоритма

На первом этапе вычислительное ядро состоит из построения графа k ближайших соседей по исходной матрице смежности (требуется для каждой вершины перебрать всех соседей и выделить k ближайших)

На втором этапе вычислительное ядро состоит из повторяющегося нахождения разбиения графа на два подграфа, удовлетворяющего ранее описанным условиям

На третьем этапе вычислительное ядро состоит из вычисления на очередном этапе метрики схожести для двух кластеров, и их последующего объединения

1.4  Макроструктура алгоритма

1. Построение графа k-ближайших соседей по исходным данным

2. Разбиения полученного на первом этапе графа на множество подграфов. На очередной итерации выбирается максимальный подграф, для него определяется оптимальное разбиение (подробнее описано в разделе 1.2), подграф разбивается в соответсвии с данным разбиением, начинается следующая итерация. В определенный момент, когда количество вершни в максимальном подграфе становится меньше, чем некоторая изначально заданная доля от количества вершин в первоначальном графе, разбиение прекращается.

3. Итеративно осуществляется обхединение подграфов, на основе метрик взаимной связности и взаимного сходства. Процесс объединения завершается в момент достижения целевых показателей по данным метрикам.

1.5 Схема реализации последовательного алгоритма

Схема представлена в виде C++-подобного псевдокода, макрооперации в алгоритме выделены в соответствии с предыдущим разделом описания.

 int n; // Количество точек.
int k; // Параметр k
int Dist[n][n]; // Матрица расстояний между точками.
 
integer E[n][n]; // Матрица рёбер графа

foreach (int i=0; i<n; i++) ) {
   integer KNeighbours[k]; // список, используемый для хранения ближайших соседей
   integer countN = 0;
   
   foreach (int j=i+1; j<n; j++ ) {
     //Заполняем список k ближайших соседей по матрице Dist
   }
 
   foreach (int j=0; j<k; j++) {
     E[i][KNeighbours[j]] = 1;
   }
 }
 return E;

double q; //Параметр, описание находится в соответствующем разделе. 
Graph g = getBiggestGraph(); //Находим граф максимального размера
int maxSize = getSize(g); //Находим размер данного графа
while (maxSize > n * q) { 
   breakGraph(g); // Разбиваем граф
}

Graph graphs[m]; //Разбиение по кластерам
while (count(graphs)>1){
   pairs_exist = false //Значение будет обновлено позже, если найдется подходящая пара для объединения
   for (int i = 0; i < m; i++) {
      for (int j = i + 1; j < m; j++) { 
         if (checkSimilarity(graphs[i],graphs[j])) { //Проверяем, достаточно ли схожи графы для объединения
			unite(graphs[i], graphs[l]) 
		 } else {
			break;
		 }
      }
   }
}

1.6  Последовательная сложность алгоритма

На первом этапе построение графа k-ближайших соседей требует [math]O(n^2)[/math] операций.

На втором этапе для итеративного разбиения требуется [math]O(nm)[/math]операций, где [math]n[/math] - количество вершин графа, а [math]m[/math] - количество подграфов в итоговом разбиении.

На третьем этапе требуется [math]O(m^2logm)[/math] операций, причем вычисление метрики считается за одну операцию.

Итоговая оценка последовательной сложности [math]O(n^2)+O(nm)+O(m^2logm)[/math]

1.7 Информационный граф

1.8 Ресурс параллелизма алгоритма

На первом этапе вычисление [math]k[/math] ближайших вершин для [math]i[/math]-й вершины можно распараллелить между [math]n[/math] процессами (это вычисление независимо для каждой вершины). На втором и третьем этапах процессы разбиения и объединения подграфов происходят последовательно. Получаем оценку параллельной сложности алгоритма [math]O(nm)+O(m^2logm)[/math]

1.9 Входные и выходные данные алгоритма

На вход алгоритму подается множество из [math]n[/math] векторов длины [math]l[/math], описывающих объекты для кластеризации. Также передаются параметры [math]k[/math] (для построения графа k ближайших соседей на первом этапе) и [math]q[/math] (используется на втором этапе для определения критерия прекращения итерационного процесса). На выходе алгоритм выдает массив длины [math]n[/math], заполненный числами от [math]1[/math] до [math]n[/math], показывающими, в какой кластер попал соответствующий объект.

1.10 Свойства алгоритма

Первый этап алгоритма хорошо распараллеливается (так как нахождение [math]k[/math] ближайших вершин для каждой вершины можно осуществлять независимо). Второй и третий этап выполняются последовательно итерация за итерацией, но возможно их частичное распараллеливание.

Вычислительная мощность (соотношение времени выполнения и объема входных и выходных данных) для разных этапов:

[math]O(1)[/math] для первого этапа

[math]O(\frac{nm}{n^2+m^2})[/math] для второго этапа

[math]O(\frac{m^2log(m)}{m^2+n})[/math] для третьего этапа

1-й этап алгоритма детерминирован (граф [math]k[/math] ближайших соседей всегда одинаков), второй и третий этапы недетерминированы (зависят от того, какие подграфы будут выбираться на итерациях алгоритма)

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

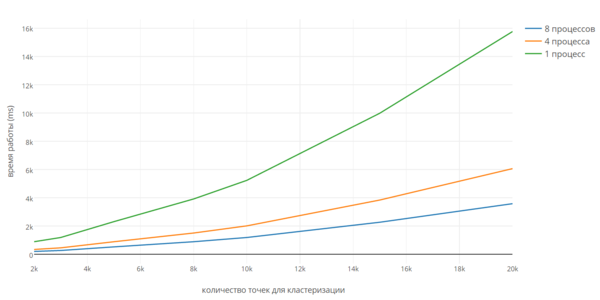
Реализации алгоритма Chameleon для систем с распределенной памятью найдено не было, но была найдена параллельная реализация для систем с общей памятью . Для данной реализации авторы приводят информацию о производительности, но не приводят исходный код программы. По этой причине была исследована масштабируемость алгоритма в зависимости от количества точек для кластеризации для реализации в пределах одного узла для реализации . Запуск программы осуществлялся на вычислительном комплексе IBM Blue Gene/P на одном узле. Характеристики узла приведены по ссылке . Далее приведены графики зависимости времени работы программы от размера входных данных. Графики для 4-х и 8 процессов оценочны.

Эффективность алгоритма убывает с ростом числа процессов. Темпы убывания эффективности растут с ростом размера входных данных.

2.7 Существующие реализации алгоритма

Одна из последовательных реализаций алгоритма находится по ссылке [1]

Параллельных реализаций алгоритма найдено не было