Участник:Janyell/Хранение ненулевых элементов разреженной матрицы. Умножение разреженной матрицы на вектор

Умножение разреженной матрицы на вектор
Последовательный алгоритм
Последовательная сложность	[math]O(nz)[/math]
Объём входных данных	[math]nz + m[/math]
Объём выходных данных	[math]n[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(m)[/math]
Ширина ярусно-параллельной формы	[math]O(n)[/math]

Авторы описания: Е.А. Сычева (разделы 1.1.1.1, 1.1.1.2, 1.1.2, 1.2 - 1.6, 1.9, 1.10) и А.С. Хахалин (разделы 1.1.1.3 - 1.1.1.6, 1.7, 1.8, 2.4, 2.7)

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Разреженная матрица — матрица с большим количеством нулевых элементов.

Среди специалистов нет единства в определении того, какое именно количество ненулевых элементов делает матрицу разреженной. Матрицу порядка [math]n[/math] называют разреженной, если число ее ненулевых элементов :

• есть [math]O(n)[/math]. Приве­денное определение полезно только для теоретических целей типа попытки оценить асимптотическое поведение алгоритма.
• ограничено в строке, в типичном случае от 2 до 10.
• выражается как [math]n^{1+\gamma}[/math], где [math]\gamma \lt 1[/math].
• таково, что для данной матрицы, данного алгоритма и данной вычислительной машины имеет смысл извлекать выгоду из на­личия в ней многих нулей.

Всякую разреженную матрицу можно обрабатывать так, как если бы она была плотной: напротив, вся­кую плотную, или заполненную, матрицу можно обрабатывать алгоритмами для разреженных матриц. В обоих случаях полу­чатся правильные численные результаты, но вычислительные затраты возрастут. Приписывание матрице свойства разреженности эквивалентно утверждению о существовании алгоритма, исполь­зующего ее разреженность и делающего вычисления с ней дешевле по сравнению со стандартными алгоритмами.

Три основных идеи, которые направляли развитие большей части технологии разреженных матриц:

• хранить только ненулевые элементы. Разреженная матрица, будучи множеством чисел, не имеющим регулярности, не может быть представлена в памяти машины тем же простым способом, что и полная матрица - регулярным числовым массивом. Поэтому возникает необходимость дополнительно хранить индексную информацию, указывающую расположение каждого элемента в регулярном массиве.
• оперировать только с ненулевыми элементами. Число операций, производимых машиной при исполнении алгоритма, пропорционально числу ненулевых элементов, а не числу всех элементов матрицы.
• сохранять разреженность. Хоро­ший алгоритм для разреженных матриц пытается сохранить раз­реженность, по возможности уменьшая заполнение.

В целях упрощения операций с разреженными матрицами многие алгоритмы разрешают также хранить небольшое количество нулевых элементов и оперировать с ними как с ненулевыми.

1.1.1 Хранение ненулевых элементов разреженной матрицы

1.1.1.1 Диагональная схема хранения ленточных матриц

Матрицу [math]A[/math] называют ленточной, если все ее ненулевые элементы заключены внутри ленты, образованной диагоналями, параллельными главной диагонали. Таким образом, [math]a_{ij} = 0[/math], если [math]|i - j| \gt b[/math], и [math]a_{k, k-b} \ne 0[/math], либо [math]a_{k, k+b} \ne 0[/math] хотя бы для одного значения [math]k[/math]. Здесь [math]b[/math] — полуширина, а [math]2b + 1[/math] — ширина ленты. Лентой матрицы [math]A[/math] называется множество элементов, для которых [math]|i - j| \leq b[/math]. Другими словами, для всякой строки [math]i[/math] ленте принадлежат все элементы со столбцовыми индексами от [math]i - b[/math] до [math]i + b[/math], т. е. [math]2b + 1[/math] элементов.

Если матрица симметрична, то достаточно хранить ее полу­ленту. Верхняя полулента состоит из элементов, находящихся в верхней части ленты, т. е. таких, что [math]0 \lt j - i \leq \beta [/math]; нижняя полулента состоит из элементов нижней части ленты, т. е. таких, что [math]0 \lt i - j \leq \beta[/math]; в обоих случаях в строке [math]\beta[/math] элементов.

С ленточными матрицами связана простейшая и наиболее широко применяемая стратегия использования нулевых элементов матрицы. Диагональная схема хранения симметричной ленточной ма­трицы [math]A[/math] порядка [math]n[/math] и полуширины ленты [math]\beta[/math] представляет собой массив [math]AN (I, J)[/math] размером [math]n \times (\beta + 1)[/math]. Главная диагональ хранится в последнем столбце, а нижние кодиагонали — в остальных столбцах со сдвигом на одну позицию вниз при каждом смещении влево.

Для несимметричной матрицы [math]A[/math] необходим массив размером [math]n \times(2\beta + 1)[/math]; нижняя полулента и главная диагональ хранятся прежним образом, а верхние кодиагонали — в правой части массива со сдвигом на одну позицию вверх при каждом смещении вправо. Диагональная схема удобна, если [math]\beta \lt \lt n [/math]. Она является схемой прямого доступа в том смысле, что имеется простое взаимно однозначное соответствие между положением элемента в матрице [math]A[/math] и его положением в массиве: [math]a_{ij}[/math] хранится компонентой [math]AN (i, j - i + \beta + 1)[/math].

1.1.1.2 Профильная схема хранения симметричных матриц

Ленточная матрица высокого порядка может иметь широкую ленту и большое число нулей внутри ее. Для такой матрицы диагональная схема может быть очень неэкономной. Профильная схема или схема переменной ленты является более эффективной схемой хранения симметричных матриц.

Для каждой строки [math]i[/math] симметричной матрицы [math]A[/math] положим:

[math]\beta_{i} = i - j_{min} (i)[/math],

где [math]j_{min} (i)[/math] — минимальный столбцовый индекс строки [math]i[/math], для которого [math]a_{ij} \ne 0[/math]. Таким образом, первый ненулевой элемент строки [math]i[/math] находится на [math]\beta_{i}[/math]- позиций левее главной диагонали.

Оболочка матрицы [math]A[/math] — это множество элементов [math]a_{ij}[/math], для которых [math]0 \lt i - j \lt \beta_{i}[/math] В строке [math]i[/math] оболочке принадлежат все элементы со столбцовыми индексами от [math]j_{min} (i)[/math] до [math]i - 1[/math], всего [math]\beta_{i}[/math] элементов. Диагональные элементы не входят в оболочку. Про­филь матрицы [math]A[/math] определяется как число элементов в оболочке:

[math]profile (A) = \sum\limits_{i}\beta_{i}[/math]

При использовании профильной схемы все элементы оболочки, упорядоченные по строкам, хранятся, включая нули, в одномер­ном массиве [math]AN[/math]. Диагональный элемент данной строки помещается в ее конец. Длина массива [math]AN[/math] равна сумме профиля и порядка [math]A[/math]. Кроме того, необходим массив указателей [math]IA[/math]; элементы этого массива - указатели расположения диагональ­ных элементов в [math]AN[/math]. Так, при [math]i \gt 1[/math] элементы строки [math]i[/math] находятся в позициях от [math]IA (i - 1) + 1[/math] до [math]IA (i)[/math]. Единственный элемент [math]a_{11}[/math] 1-й строки хранится в [math]AN (1)[/math].

Схема переменной ленты строчно-ориентирована в том смысле, что любая строка матрицы сканируется эффективно; в то же время всякая попытка сканировать столбцы будет неэффективной. Кроме того, схема является статической - заготовленной до начала численной обработки, - потому что включение нового элемента, лежащего вне оболочки, требует изменения всей структуры.

1.1.1.3 Связные схемы разреженного хранения

Рассмотрим разреженную матрицу [math]A[/math]. Ее ненулевые элементы, которых очень мало в сравнении с числом нулей, рассеяны по всей матрице, образуя портрет матрицы или шаблон нулей—ненулей. Опишем схему хранения предложенную Кнутом. Ненулевые элементы хранятся в компактной форме и в произвольном порядке в одномерном массиве [math]AN[/math]. Информация о положении элементов может храниться двумя дополнительными параллельными одномерными массивами [math]I[/math] и [math]J[/math]; здесь для каждого ненулевого элемента содержатся его строчный и столбцовый индексы. Таким образом, для каждого [math]a_{ij}\ne0[/math] в памяти находится тройка [math](a_{ij},i,j)[/math]. Далее, чтобы можно было легко отыскать элементы произвольной строки или столбца, необходимы ещё пара указателей для каждой тройки, а также указатели входа для строк и столбцов, сообщающие начало каждого строчного или столбцового списка. Пусть [math]NR[/math] ("next nonzero element in the same row" — "следующий ненулевой элемент той же строки") — массив, хранящий строчные указатели, а [math]NC[/math] ("next nonzero element in the same column" — "следующий ненулевой элемент того же столбца") — массив столбцовых указателей. Пять массивов [math]AN,I,J,NR,NC[/math] имеют общую длину, и их одноименные позиции соответствуют друг другу. Пусть [math]JR[/math] и [math]JC[/math] — массивы, содержащие указатели входа для строк и столбцов, расположенные в соответствии с порядком строк и столбцов матрицы. Тогда, например, для просмотра [math]i[/math] строки необходимо:

1. определить входной индекс [math]j=JR[i][/math]
2. определить элемент [math]AN[j][/math]
3. найти индекс следующего элемента [math]j=NR[j][/math]
4. если [math]j=0[/math], то мы обошли все элемент [math]i[/math]-ой строки, иначе, перейти в п.2

Заметим, что рассмотренная схема требует пять ячеек памяти для каждого ненулевого элемента, а также 2 массива указателей входа для строк и столбцов. Вследствие большой накладной памяти такая схема весьма неэкономна. Достоинства её в том, что в любом месте можно включить или исключить элемент, а также можно эффективно сканировать строки и столбцы.

1.1.1.4 Разреженный строчный формат

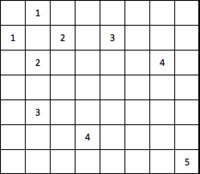
Рассмотрим матрицу [math]A[/math](рис. 1).

Рисунок 1. Матрица A

Значения ненулевых элементов и соответствующие столбцовые индексы хранятся в этой схеме по строкам в двух массивах — [math]AN[/math] и [math]JA[/math] соответственно. Дополнительно также используется массив указателей [math]IA[/math], отмечающих позиции массивов [math]AN[/math] и [math]JA[/math], с которых начинается описание очередной строки. Дополнительная компонента в [math]IA[/math] содержит указатель первой свободной позиции в [math]AN[/math] и [math]JA[/math]. В общем случае описание [math]r[/math]-й строки [math]A[/math] хранится в позициях с [math]IA (r)[/math] до [math]IA (r + 1) - 1[/math] массивов [math]JA[/math] и [math]AN[/math], за исключением равенства [math]IA (r + 1) = IA (r)[/math], означающего, что [math]r[/math]-я строка пуста. Если матрица [math]A[/math] имеет [math]m[/math] строк, то [math]IA[/math] содержит [math]m + 1[/math] позиций.

Рисунок 2. Формат RR (C) O на примере матрицы А(рис.1)

Данный способ представления называют полным, поскольку представлена вся матрица [math]A[/math], и упорядоченным, поскольку элементы каждой строки хранятся в соответствии с возрастанием столбцовых индексов. Таким образом, это строчное представление, полное и упорядоченное, или сокращенно RR (C) O (рис. 2). Сокращенное название данного формата происходит от английского словосочетания "Row - wise Representation Complete and Ordered" (строчное представление, полное и упорядоченное).

Схема предъявляет минимальные требования к памяти и в то же время оказывается очень удобной для нескольких важных операций над разряженными матрицами: сложения, умножения, перестановок строк и столбцов, транспонирования, решения линейных систем с разреженными матрицами коэффициентов как прямым, так и итерационными методами.

1.1.1.5 Неупорядоченные представления

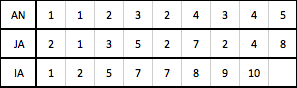
Рассмотрим формат RR(C)U (рис. 3). Сокращенное название данного формата происходит от английского словосочетания "Row - wise Representation Complete and Unordered" (строчное представление, полное, но неупорядоченное).

Аналогично RR(C)O формат RR(C)U представлен тремя массивами — [math]AN,JA,IA[/math], но элементы в массивах [math]AN,JA[/math] относящиеся к одной строке, могут идти в произвольном порядке.

Рисунок 3. Формат RR (C) U на примере матрицы А (рис.1)

Формат RR(C)U вводится по следующим причинам. Представления разреженных матриц необязательно должны быть упорядочены в том смысле, что, хотя упорядоченность строк соблюдается, внутри каждой строки элементы исходных матриц могут храниться в произвольном порядке. Такие неупорядоченные представления могут быть весьма удобны в практических вычислениях. Результаты большинства матричных операций получаются неупорядоченными, а их упорядочение стоило бы значительных затрат машинного времени. В то же время, за немногими исключениями, алгоритмы для разреженных матриц не требуют, чтобы их представления были упорядоченными.

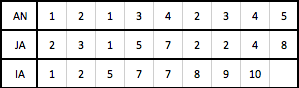
Ещё одним форматом неупорядоченного представления является RR (U) U (рис. 4). Сокращенное название формата RR (U) U происходит от английского словосочетания "Row - wise Representation, Upper, Unordered" (строчное представление, верхний треугольник, неупорядоченное).

Рисунок 4. Формат RR (U) U на примере матрицы А (рис.1)

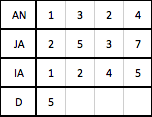
Данный формат используется для симметричных и верхних треугольных матриц, у которых большинство диагональных элементов отличны от нуля. В этом формате представляется только верхний треугольник матрицы (внутри каждой строки элементы могут храниться в произвольном порядке), а ее диагональные элементы хранятся в отдельном одномерном массиве. Верхняя треугольная матрица представляется тремя массивами [math]AN,JA,IA[/math], которые аналогичны массивам в формате RR(C)U.

1.1.1.6 Хранение блочных матриц

Идея разбиения большой матрицы на подматрицы или блоки возникает естественным образом. С блоками можно обращаться, как если бы они были элементами матрицы, и блочная матрица превращается в матрицу из матриц. Разбиение на блоки играет важную роль в технологии разреженных матриц, потому что многие алгоритмы, сконструированные первоначально для числовых матриц, можно обобщить на случай матриц из матриц. Большая гибкость, связанная с понятием разбиения, может давать определенные вычислительные преимущества. С другой стороны, разбиение можно рассматривать просто как инструмент управления данными, помогающий организовать обмен информацией между оперативной памятью и внешними запоминающими устройствами.

Хранение блочной матрицы подразумевает хранение множества её подматриц. Рассмотрим неявную схему хранения, предназначенную главным образом для симметричных матриц с квадратными диагональными блоками. Диагональные блоки рассматриваются так, как если бы они составляли единую матрицу, и хранятся в соответствие с профильной схемой. Численные значения элементов хранятся по строкам в массиве [math]AN[/math], а указатели на диагональные элементы каждой строки — в целом массиве [math]IA[/math]. Поддиагональные блоки рассматриваемые так, как если бы они составляли единую матрицу, хранятся посредством разреженного строчного формата. Ненулевые элементы размещаются по строкам в вещественном массиве [math]AP[/math], а соответствующие столбцовые индексы — в параллельном целом массиве [math]JA[/math]. Указатели начала строк хранятся в массиве [math]IP[/math].

1.1.2 Умножение разреженной матрицы на вектор

Умножение разреженной матрицы на вектор используется при вычислении векторов Ланцоша, необходимом при итерационном решении линейных уравнений методом сопряженных градиентов, а также при вычислении собственных значений и собственных векторов матрицы. Достоинство этих процедур, с вычислительной точки зрения, состоит в том, что единственная требуемая матрич­ная операция — это повторное умножение матрицы на последо­вательность заполненных векторов; сама матрица не меняется. Следовательно, наиболее релевантными для этих задач являются статические схемы хранения.

В зависимости от формы представления матрицы используются различные алгоритмы. Далее рассмотрим простейший случай — это когда матрица, прямоугольная или квадратная, хранится в форме RR (С) U.

1.2 Математическое описание алгоритма

Исходные данные: разреженная матрица общего вида [math]A[/math] (элементы [math]a_{ij}[/math], [math]i = 1, \ldots, n[/math], [math]j = 1, \ldots, m[/math]), заполненный вектор-столбец [math]b[/math] (элементы [math]b_{j}[/math], [math]j = 1, \ldots, m[/math])

Вычисляемые данные: заполненный вектор-столбец [math]c[/math] (элементы [math]c_{i}[/math], [math]i = 1, \ldots, n[/math]).

Формулы метода:

[math]c_{i} = \sum\limits_{k = 1}^{nz{_i}} a_{i,j=j(k)}b_{j=j(k)}[/math],

где [math]nz{_i}[/math] - количество ненулевых элементов [math]a_{ij}[/math], [math]j = 1, \ldots, m[/math],

[math]j = j(k)[/math] - индексная информация, указывающая расположение ненулевого элемента [math]a_{ij}[/math], [math]i = 1, \ldots, n[/math] и соответствующего элемента [math]b_{j}[/math].

Существует также блочная версия метода, однако в данном описании разобран только точечный метод.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро умножения разреженной матрицы на вектор можно составить из множественных (всего их [math]n[/math]) вычислений скалярных произведений вектор-строк [math]a^i[/math] (элементы [math]a^i_{k}[/math], [math]k = 1, \ldots, nz_{i}[/math]), состоящих из ненулевых элементов [math]a_{i, j=j(k)}[/math], на вектор-столбцы [math]b^i[/math] (элементы [math]b^i_{k}[/math], [math]k = 1, \ldots, nz_{i}[/math]), состоящих из элементов [math]b_{j=j(k)}[/math], [math]i = 1, \ldots, n[/math]:

[math]\sum\limits_{k = 1}^{nz_{i}} a^i_k b^i_k[/math]

в режиме накопления или без него, в зависимости от требований задачи.

1.4 Макроструктура алгоритма

Как записано и в описании ядра алгоритма, основную часть метода составляют множественные (всего [math]n[/math]) вычисления сумм:

[math]\sum\limits_{k = 1}^{nz_{i}} a^i_k b^i_k[/math]

в режиме накопления или без него.

1.5 Схема реализации последовательного алгоритма

Последовательность исполнения метода следующая:

Далее описывается простейший случай — матрица [math]A[/math] хранится в форме RR (С) U.

1. [math]k^0_{nz} = IA(1)[/math]

Далее для всех [math]i[/math] от [math]1[/math] до [math]n[/math] по нарастанию выполняются

2. [math]c_i = 0[/math]

3. [math]k^i_0 = k^{i - 1}_{nz}[/math]

4. [math]k^i_{nz} = IA(i + 1) - 1[/math]

5. [math]c_{i} = \sum\limits_{k = k^i_0}^{k^i_{nz}} AN(k) b_{JA(k)}[/math]

После этого (если [math]i \le n[/math]) происходит переход к шагу 2 с бо́льшим [math]i[/math].

Особо отметим, что вычисления [math]c_{i}[/math] производят в режиме накопления сложением произведений [math]AN(k) b_{JA(k)}[/math] для [math]k[/math] от [math]k^i_0[/math] до [math]k^i_{nz}[/math], c нарастанием [math]k[/math].

1.6 Последовательная сложность алгоритма

Для алгоритма умножения разреженной матрицы размером [math]n \times m[/math], представленной в формате RR (C) U, на вектор длины [math]m[/math] в последовательном (наиболее быстром) варианте требуется:

• [math]nz[/math] сложений (вычитаний),
• [math]nz[/math] умножений,

где [math]nz[/math] - количество ненулевых элементов матрицы [math]A[/math].

Умножения и сложения (вычитания) составляют основную часть алгоритма.

При этом использование режима накопления требует совершения умножений и вычитаний в режиме двойной точности, что ещё больше увеличивает долю умножений и сложений/вычитаний во времени, требуемом для выполнения умножения разреженной матрицы на вектор.

При классификации по последовательной сложности, таким образом, алгоритм умножения разреженной матрицы на вектор относится к алгоритмам со сложностью [math]O(nz)[/math].

1.7 Информационный граф

Опишем граф алгоритма как аналитически, так и в виде рисунка. Далее предполагается, что матрица [math]A[/math] представлена в формате RR (C) U.

Граф алгоритма состоит из двух групп вершин, расположенных в целочисленных узлах двух областей.

Первая группа вершин расположена в двумерной области, соответствующая ей операция [math]a*b[/math]. Естественно введённые координаты области таковы:

• [math]i[/math] — меняется в диапазоне от 1 до [math]k[/math], принимая все целочисленные значения;
• [math]j[/math]— меняется в диапазоне от 1 до [math]n[/math], принимая все целочисленные значения.

Здесь [math]k[/math] зависит от [math]j[/math] и соответствует числу ненулевых элементов в [math]j[/math]-ой строке матрицы [math]A[/math], которое равно [math]IA[j+1] - IA[j][/math].

Аргументы операции следующие:

• [math]a[/math] — элемент массива [math]AN[/math] с индексом [math]IA_{j} + i[/math];
• [math]b[/math] — элемент входного вектора [math]b[/math] с индексом [math]JA[IA_{j} + i][/math].

Вторая группа вершин расположена в двумерной области, соответствующая ей операция [math]a+b[/math]. Естественно введённые координаты области таковы:

• [math]i[/math] — меняется в диапазоне от 3 до [math]k+1[/math], принимая все целочисленные значения;
• [math]j[/math]— меняется в диапазоне от 1 до [math]n[/math], принимая все целочисленные значения.

Здесь [math]k[/math] зависит от [math]j[/math] и соответствует числу ненулевых элементов в [math]j[/math]-ой строке матрицы [math]A[/math], которое равно [math]IA[j+1] - IA[j][/math].

Аргументы операции следующие:

• [math]a[/math]:
  • при [math]i=3[/math] — результат срабатывания операции, соответствующей вершине из первой группы, с координатами [math]i - 2, j[/math];
  • при [math]i\gt 3[/math] — результат срабатывания операции, соответствующей вершине из второй группы, с координатами [math]i - 1, j[/math];
• [math]b[/math] — результат срабатывания операции, соответствующей вершине из первой группы, с координатами [math]i - 1, j[/math].

Результат срабатывания операции является промежуточным данным алгоритма.

Описанный граф можно посмотреть на рис. 5. Граф отображает параллельную версию произведения разреженной матрицы на вектор, где каждая строка показывает ядро алгоритма (произведение строки на вектор). Вершины, соответствующие входным и выходным данным обозначены прямоугольниками, а вершины, соответствующие операциям — окружностями. Здесь вершины первой группы обозначены зеленым цветом и буквосочетанием multi, вершины второй — синим цветом и знаком сложения.

Рисунок 5. Граф алгоритма. multi — произведение.

1.8 Ресурс параллелизма алгоритма

Для алгоритма умножения разреженной матрицы размером [math]n\times m[/math], представленной в формате RR (C) U, на вектор длины [math]m[/math] в параллельном варианте требуется последовательно выполнить следующие ярусы:

• по [math]nz_{\max}[/math] ярусов умножений и сложений (в каждом из ярусов — [math]n[/math] операций),

где [math]nz_{\max} = \max_{1 \leq i \leq n} nz_i \leq m[/math].

При этом использование режима накопления требует совершения умножений и сложений в режиме двойной точности, а в параллельном варианте это означает, что практически все промежуточные вычисления для выполнения алгоритма в режиме накопления должны быть двойной точности. В отличие от последовательного варианта это означает некоторое увеличение требуемой памяти.

При классификации по высоте ЯПФ, таким образом, алгоритм умножения разреженной матрицы на вектор относится к алгоритмам с линейной сложностью. При классификации по высоте ЯПФ его сложность также будет линейной.

1.9 Входные и выходные данные алгоритма

Входные данные:

• разреженная матрица общего вида [math]A[/math] (элементы [math]a_{ij}[/math], [math]i = 1, \ldots, n[/math], [math]j = 1, \ldots, m[/math]), заданная в формате RR (C) U;

• заполненный вектор-столбец [math]b[/math] (элементы [math]b_{j}[/math], [math]j = 1, \ldots, m[/math]).

Объём входных данных:

• [math]nz[/math] (без учета индексной информации, составляющей накладные расходы - массивы [math]JA, IA[/math]);

• [math]m[/math].

Выходные данные: заполненный вектор-столбец [math]c[/math] (элементы [math]c_{i}[/math], [math]i = 1, \ldots, n[/math]).

Объём выходных данных: [math]n[/math].

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов равно [math]O(\frac{nz}{n})[/math].

При этом вычислительная мощность алгоритма умножения разреженной матрицы на вектор, как отношение числа операций к суммарному объему входных и выходных данных – константа.

При этом алгоритм умножения матрицы на вектор полностью детерминирован. Использование другого порядка выполнения ассоциативных операций в данной версии нами не рассматривается.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

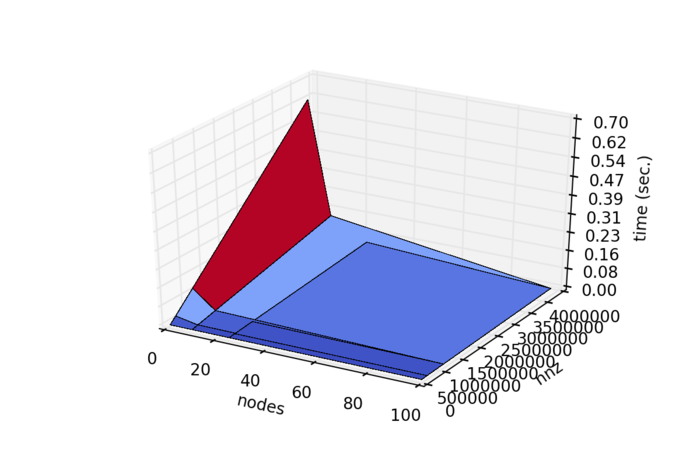
Проведём исследование масштабируемости параллельной реализации умножения разреженной матрицы в формате RR(C)U на вектор. Исследование проводилось на вычислительном комплексе IBM Blue Gene/P. В качестве программной реализации была использована модифицированная версия программы.

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

• число процессоров [1, 10, 25, 50, 100]
• количество ненулеввых элементов в матрице [1500, 40000, 150000, 600000, 3750000].

На следующем рисунке приведен график времени выполнения выбранной реализации умножение разреженной матрицы в формате RR(C)U на вектор в зависимости от изменяемых параметров запуска.

Рисунок 6. Параллельная реализация умножение разреженной матрицы в формате RR(C)U на вектор.

Можно заметить, что скорость вычисления при переходе с последовательной на параллельную версию возросла значительно. В то время как дальнейшее увеличение числа вычислительных устройств не дает такого эффекта. Это объясняется быстрым ростом накладных расходов на организацию параллельного выполнения. Это подтверждает предположение о том, что накладные расходы начинают сильно превалировать над вычислениями.

2.7 Существующие реализации алгоритма

Алгоритм умножения разреженной матрицы на вектор входит в состав таких библиотек для вычислений с разреженными матрицами, как: SparseLib++[1], uBLAS [2], Intel MKL [3], cuSPARSE [4] и др.

3 Литература

<references \>