Участник:Khotkin/Построение матрицы Адамара произвольного размера

Эта работа прошла предварительную проверку Дата последней правки страницы: 15.12.2016 Данная работа соответствует формальным критериям. Проверено Sleo.

Построение матрицы Адамара
Последовательный алгоритм
Последовательная сложность	[math]O(m2^{2m})[/math]
Объём входных данных	[math]1[/math]
Объём выходных данных	[math]2^{2n}[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(1)[/math]
Ширина ярусно-параллельной формы	[math]O(2^{2n})[/math]

Основные авторы описания: Хоткин Кирилл 623 гр., Царев Михаил 615 гр.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Матрица Адамара [math]H[/math] порядка [math]n[/math] представляет собой матрицу размера n×n из элементов [math]+1[/math] и [math]-1[/math], такую, что: [math]H \cdot H^T = n \cdot E_n,[/math] где [math]E_n[/math] — это единичная матрица размера n×n.

Матрицы Адамара находят широкое применение в теории кодирования (коды, исправляющие ошибки), теории планирования многофакторных экспериментов (ортогональные блок-схемы), квантовой информатике и прочих областях.

Матрица Адамара остаётся матрицей Адамара при следующих преобразованиях:

• умножение строчки или столбца на −1;
• перестановка строчек или столбцов местами.

Матрицы Адамара, получаемые друг из друга многократным применением указанных выше преобразований называются эквивалентными.

Матрица Адамара называется нормализованной, если её первая строка и столбец состоят только из единиц.

Под матрицией Адамара [math]H_m[/math] подразумевается матрица порядка [math]2^m[/math]

Примерами матриц Адамара различных размеров являются следующие матрицы:

[math]H_0 = (1);[/math]

[math]H_1 = \begin{pmatrix} 1 & 1 \\1 & -1 \end{pmatrix}; [/math]

[math]H_2 = \begin{pmatrix} 1 & 1 & 1 & 1 \\1 & -1 & 1 & -1 \\1 & 1 &- 1 & -1 \\1 & -1 & -1 & 1 \end{pmatrix}. [/math]

Вообще, если [math]H_m[/math] матрица Адамара порядка [math]2^m[/math], то матрица [math]H_{m+1} = \begin{pmatrix} H_m & H_m \\H_m & -H_m \end{pmatrix} [/math] является матрицей Адамара порядка [math]2^{m+1}[/math]

Кроме того, матрицу Адамара порядка [math]2^m[/math] можно получить по следующей формуле [math]H^{\otimes m} = H_1 \otimes ... \otimes H_1[/math], где знак [math] \otimes [/math] означает тензорное произведение.

Также существует недоказанная гипотеза Адамара, которая утверждает, что существуют матрицы Адамара порядка [math]4k[/math] для любого натурального [math]k[/math], однако матрица Адамара порядка [math]268[/math] до сих пор не построена, как и для ряда других порядков больше [math]268[/math]. Поэтому в данной работе будут рассматриваться матрицы Адамара порядка [math]2^m[/math].

1.2 Математическое описание алгоритма

Описанные ранее способы построения матрицы Адамара не являются оптимальными, поэтому вычисление матрицы Адамара порядка [math]2^m[/math] будет производится поэлементно с помощью следующей формулы:

[math] (H_m)_{ij}=(-1)^ {\sum_{k}{(i \& j)_k}}, [/math]

где [math]\& - [/math] побитовая операция И,

[math](i \& j)_k - [/math] [math]k[/math] -ый разряд в двоичном представлении числа [math](i \& j)[/math].

1.3 Вычислительное ядро алгоритма

Вычислительным ядром алгоритма является вычисление элементов матрицы Адамара:

[math] (H_m)_{ij}=(-1)^ {\sum_{k}{(i \& j)_k}}. [/math]

1.4 Макроструктура алгоритма

Как и в описании ядра алгоритма, основной частью алгоритма является вычисления очередного элемента матрицы Адамара с помощью следующего выражения:

[math](-1)^ {\sum_{k}{(i \& j)_k}}.[/math]

1.5 Схема реализации последовательного алгоритма

Для вычисления очередного элемента матрицы Адамара нужно выполнить следующие шаги:

1. Побитовое умножение [math]i[/math] и [math]j[/math]:  [math]result = i \& j [/math] ;

2. Нахождение числа единиц в двоичной записи числа [math]result [/math]: [math] sum = \sum_{k}{(result)_k} [/math];

3. Нахождение элемента матрицы Адамара: [math](H_m)_{ij}=(-1)^{sum}[/math].

Возможная реализация на языке C++:

int get_sign(unsigned N) {
    int i;
    for (i=0; N; N>>=1) { i+=N&1;}
    return (i&1) ? -1 : 1;
}
void adamar(int **e, int size) {
    for (unsigned int i = 0; i < size; ++i)
        for (unsigned int j = 0; j < size; ++j)
            e[i][j]=get_sign(i&j);
}

1.6 Последовательная сложность алгоритма

Для выполнения первого шага алгоритма для всех элементов матрицы Адамара необходимо суммарно выполнить:

• [math]2^{2m}[/math] операций побитового умножения.

На втором шаге алгоритма необходимо выполнить для каждого элемента матрицы Адамара:

• от 0 до m или m логических сдвигов на один бит в зависимости от программной реализации;
• от 0 до m или m операций сложения в зависимости от программной реализации;
• от 0 до m или m операций логического умножения в зависимости от программной реализации.

На третьем шаге для всех элементов необходимо сумарно выполнить:

• [math]2^{2m}[/math] операций побитового умножения;
• [math]2^{2m}[/math] операций сравнения с нулем.

Взяв в расчет не самую лучшую программную реализацию второго шага, всего потребуется выполнение следующего количества операций:

• [math](m+2)2^{2m}[/math] операций логического умножения;
• [math]m\cdot2^{2m}[/math] операций сложения;
• [math]m\cdot2^{2m}[/math] операций логического сдвига на один бит;
• [math]2^{2m}[/math] операций сравнения с нулем.

Всего [math](3m+3)2^{2m}[/math] операций.

1.7 Информационный граф

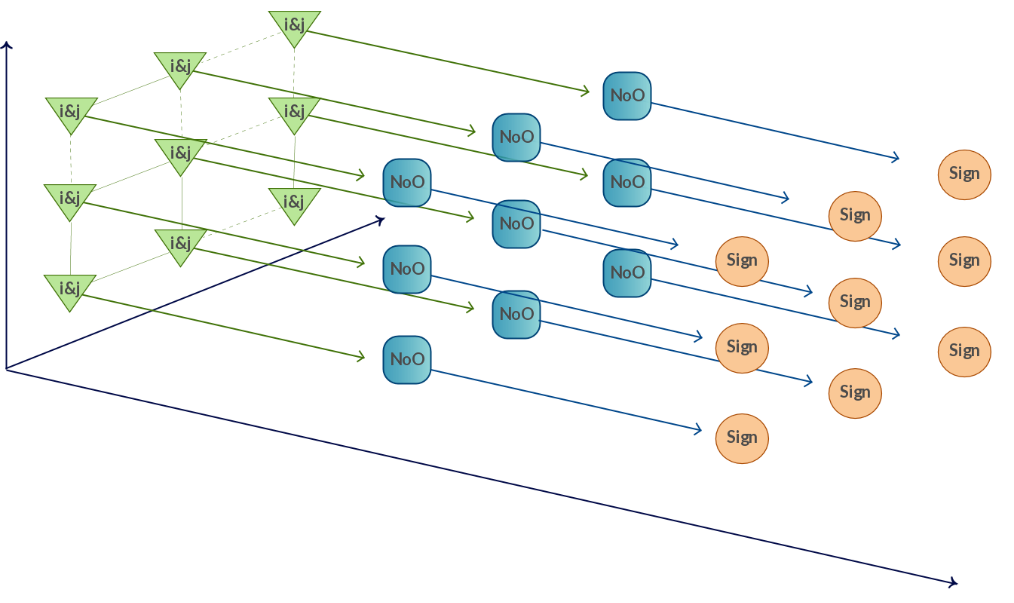
На рисунке ниже изображен информационный граф алгоритма.

• [math]i\&j[/math] - операция побитового умножения, где [math]i[/math] и [math]j[/math] соответствующие координаты элемента [math]h_{ij}[/math];
• NoO (number of ones) - вычисление количества единиц числа в двоичной системе. Состоит из последовательного применения операций сложения и побитового умножения;
• Sign - определение знака соответствующего элемента. Если результат предыдущего шага - чётное число, то знак положительный, иначе - отрицательный.

Рисунок 1. Граф алгоритма построения матрицы Адамара.

1.8 Ресурс параллелизма алгоритма

Вычисление любого элемента можно производить независимо от других, то есть параллельно.

Высота канонической ярусно-параллельной формы равна 3. Ширина ЯПФ равна [math]2^{2m}[/math].

1.9 Входные и выходные данные алгоритма

Входные данные: m - размерность матрицы [math]H_m[/math].

Объём входных данных: 1 (число m).

Выходные данные: матрица Адамара [math]H_{m}[/math] размерностью [math]2^m[/math].

Объём выходных данных: [math]2^{2m}[/math].

1.10 Свойства алгоритма

• Вычислительная мощность алгоритма построения матрицы Адамара, как отношение числа операций к суммарному объему входных и выходных данных:

[math]\,\frac{(3m+3)2^{2m}}{1+2^{2m}}\, \approx 3m+3.[/math];

• Алгоритм построения матрицы Адамара является недетерминированным, так как число операций меняется в зависимости от входных данных (числа m, которое формирует матрицу размерности 2^m × 2^m);
• Данный алгоритм построения матрицы Адамара является несбалансированным. Так как каждый элемент матрицы может обрабатываться независимо от других, вычисление элементов можно распределить по процессам. В случае, когда количество элементов матрицы [math]n[/math] не кратно количеству процессов [math]s[/math], на некоторые процессы ложится дополнительная задача вычисления элементов матрицы в количестве [math]a=n\operatorname{mod}s[/math].

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

Учитывая, что рассматриваемый алгоритм строит симметричные матрицы Адамара, можно уменьшить количество вычисляемых элементов c [math]2^{2n}[/math] до [math]\frac{2^n+2^{2n}}{2}[/math] путем вычисления только диагональных и наддиагональных элементов.

2.4 Масштабируемость алгоритма и его реализации

В ходе данной работы все вычислительные эксперименты были проведены на суперкомпьютере IBM Blue Gene/P. В суперкомпьютере насчитывается 2048 вычислительных узлов. Каждый вычислительный узел состоит из одного четырехъядерного PowerPC 450 процессора. Таким образом всего насчитывается 8192 процессорных ядер. Пиковая производительность составляет 27,9 терафлопс. На вычислительных узлах системы Blue Gene/P возможны три режима исполнения процессов: 1. режим симметричного мультипроцессора (symmetrical multiprocessing, SMP) 2. режим виртуальных вычислительных узлов (virtual node mode, VN) 3. режим двухъядерных вычислительных узлов (dual node mode, DUAL) Таким образом на вычислительном узле могут быть размещены один, четыре и два MPI процесса. В VN и DUAL режимах процессы в рамках вычислительного узла для обмена данными могут использовать механизм общей памяти. Вычислительный эксперимент проводился в режиме SMP.

Параметрами запуска реализации алгоритма были число процессов и порядок матрицы, которые менялись в диапазонах [[math]2^0, 2^1,..., 2^i,..., 2^{10}[/math]] и [[math]2^5, 2^6,..., 2^j,..., 2^{14}[/math]] соответственно. При осуществлении реализации алгоритма на каждом узле компьютера размещалось по одному процессу, таким образом при увеличении числа процессов увеличивалось и число задействованных узлов.

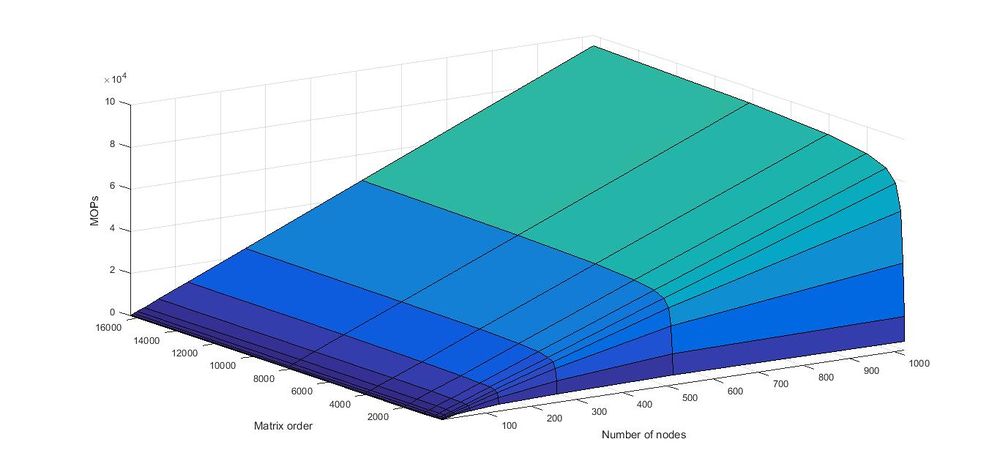
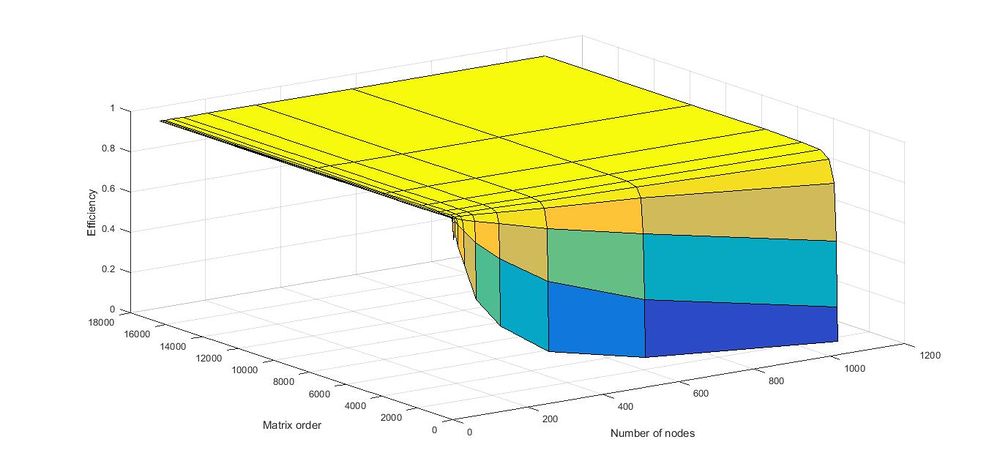
На рисунках ниже представлены графики производительности и эффективности параллелизма реализации алгоритма построения матрицы Адамара произвольного размера.

Рисунок 2. График производительности реализации алгоритма.

Рисунок 3. График эффективности параллелизма реализации алгоритма.

Построим оценки масштабируемости выбранной реализации построения матрицы Адамара:

• По числу процессов: при увеличении числа процессов производительность увеличивается практически линейно за исключением случаев, когда обрабатываются матрицы, маленьких порядков: в таких случаях время, уходящее на синхронизацию процессов, занимает значительную долю от общего времени построения матрицы. Эффективность параллелизма также не улучшается при расчёте матриц маленьких порядков. При вычислении матриц Адамара больших порядков можно наблюдать, что эффективность параллелизма реализации алгоритма равна единице или близка к ней.
• По размеру задачи: при увеличении порядка матрицы производительность и эффективность параллелизма увеличиваются несущественно.

2.7 Существующие реализации алгоритма

Примеры вычислительных пакетов, содержащих функции генерации матриц Адамара:

1. MATLAB;
2. WOLFRAM;
3. Python;
4. Octave;

Стоит отметить, что во многих вычислительных пакетах встроена операция тензорного произведения матриц, которая позволяет строить матрицу Адамара по определению. Этот факт позволяет использовать матрицу Адамара в этих вычислительных пакетах:

1. MAPLE;
2. MATCATH;

3 Литература

[1] Кронберг, Ю.И. Ожигов, А.Ю. Чернявский — Алгебраический аппарат квантовой информатики 2