Участник:Kirillov\Графо-ориентированный алгоритм кластеризации CHAMELEON

Авторы: Кириллов Валентин Владимирович, Холопкин Степан Андреевич

Графо-ориентированный алгоритм кластеризации CHAMELEON
Последовательный алгоритм
Последовательная сложность	[math]O(n^2+nm+n log n + m^2 log(m))[/math]
Объём входных данных	[math]n[/math]
Объём выходных данных	[math]n[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(log(n))[/math]
Ширина ярусно-параллельной формы	[math]O(n)[/math]

1 ЧАСТЬ. Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Алгоритм CHAMELEON первые представлен в 1999 департаментом компьютерных наук и инженерии, университет Миннесоты, США. Авторы George Karypis, Eui-Hong (Sam) Han, Vipin Kumar.

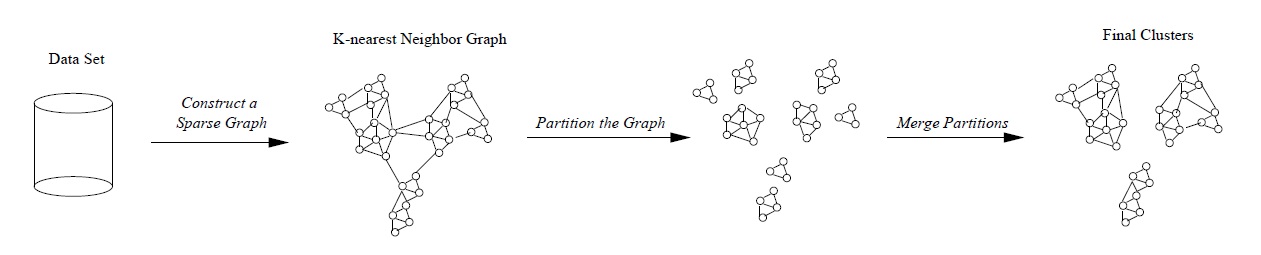
Кластеризация – процесс разбиения множества данных по некоторому признаку на такие группы, что в пределах одной группы данные максимально схожи по данному признаку, а в разных группах данные максимально различны. Иерархические алгоритмы кластеризации строят не одно разбиение множества данных на кластеры, а систему вложенных разбиений. CHAMELEON является агломеративным методом (снизу вверх), когда после первого разбиения на мелкие кластеры пары близлежащих кластеров итеративно объединяются в общий кластер. На первом этапе CHAMELEON использует алгоритм разделения графа для получения набора относительно малых кластеров. На втором этапе, для объединения кластеров, полученных на первом этапе, в настоящие кластеры, используется иерархическая агломеративная кластеризация. Таким образом, алгоритм, фактически, является гибридным, построенным комбинацией графо-ориентированных и классических иерархических методов.

На первом этапе, согласно графо-ориентированному подходу, происходит построение графа на матрице сходства объектов по принципу k ближайших соседей. Две вершины такого графа соединяет ребро, если объект, соответствующий любой из этих вершин попадает в число k наиболее близких объектов для объекта, соответствующего другой вершине из данной пары.

На рисунке изображены: объекты в пространстве – слева, граф по принципу 1-го ближайшего соседа – в середине, граф по принципу 3-х ближайших соседей – справа.

Далее, алгоритм разделяет полученный граф на множество сравнительно малых подграфов. Разделение происходит последовательно. На каждом шаге выбирается подграф, содержащий наибольшее число вершин. Этот граф разделяется на два подграфа, так, что разделитель ребер графа минимален и каждый из получаемых подграфов содержит не менее некоторого процента вершин исходного графа. Процесс разделения останавливается, когда наибольший подграф содержит меньше некоторого заданного числа вершин. Полученное множество связных графов считается множеством начальных кластеров, на котором требуется провести последовательное иерархическое объединение.

На втором этапе, алгоритм последовательно объединяет кластеры, используя значение их относительной взаимной связности и относительного взаимного сходства. Только если оба эти значения достаточно высоки у двух кластеров, они объединяются.

Относительная взаимная связность пары кластеров определяется абсолютной взаимной связностью кластеров, нормализованной с учетом внутренней связности каждого кластера (подграфа). Нормализация используется для того, чтобы исключить тенденцию к преимущественному объединению крупных кластеров, у которых, определенно, значение взаимной связности будет больше, вследствие их размера.

На рисунке представлена схема работы алгоритма CHAMELEON.

1.2 Математическое описание алгоритма

Исходные данные: набор данных (точек) произвольной размерности.

Выходные данные: набор кластеров, то есть групп исходных данных.

Шаги алгоритма:

1) Представление набора данных в виде [math]G = (V, E)[/math] с помощью алгоритма [math]k[/math]-ближайших соседей: [math]e = (v_i, v_j) \in E[/math], если [math]dist(v_i, v_j) \in sorted(\{r | r = dist(v_i, v_k), k = 1,...,n\})[1..k][/math], причем [math]weight(e) = dist(v_i, v_j)[/math]

2) Разбиение графа на небольшие кластеры. Для этого необходимо создать множество [math]C = G[/math] и выполнять цикл со следующими шагами на каждой его итерации:

• Найдем [math]C_{greatest}[/math] такой, что [math]|C_{greatest}| = \max_{1 \leq j \leq |C|}|C_j|[/math]

• Если [math]\frac{|C_{greatest}|}{|V|} \gt MINSIZE[/math], то разделить [math]C_{greatest}[/math] на 2 кластера [math]C_1[/math] и [math]C_2[/math], удалить [math]C_{greatest}[/math] из [math]C[/math], и добавить [math]C_1[/math] и [math]C_2[/math] в [math]C[/math].

• В противном случае завершил цикл.

3) Создать начальный набор кластеров [math]C_{current} = C[/math]. Затем выполнять цикл со следующими шагами на каждой итерации:

• Для каждой пары кластеров [math]C_i, C_j \in C_{current}[/math] вычислить следующие показатели:
  • [math]EC(C_i, C_j) = \sum_{e \in conn(C_i, C_j)}weight(e)[/math], где [math]conn(C_i, C_j) = \{(v, w) | v \in C_i, w \in C_j\}[/math]
  • [math]EC(C_i) = \sum_{e \in mincut(C_i)}weight(e)[/math], где [math]mincut(C_i)[/math] - минимальный разрез [math]C_i[/math]. Аналогичным образом вычислить [math]EC(C_j)[/math].
  • [math]\bar{S}_{EC(C_i, C_j)} = \frac{EC(C_i, C_j)}{|conn(C_i, C_j)|} [/math]
  • [math]\bar{s}_{EC(C_i)} = \frac{EC(C_i)}{|mincut(C_i)|}[/math]
• Вычислить относительную взаимную связность и относительное взаимное сходство двух текущих кластеров:
  • [math]RI(C_i, C_j) = \frac{|EC(C_i,C_j)|}{\frac{|EC(C_i)| + |EC(C_j)|}{2}}[/math]
  • [math]RC(C_i, C_j) = \frac{\bar{S}_{EC(C_i,C_j)}}{\frac{|C_i|}{|C_i|+|C_j|}\bar{S}_{EC(C_i)} + \frac{|C_j|}{|C_i|+|C_j|}\bar{S}_{EC(C_j)}}[/math]
• Если [math]RI(C_i, C_j)^\alpha RC(C_i, C_j) \gt t[/math], то слить данную пару кластеров, иначе - перейти к следующей паре. Здесь [math]\alpha[/math] - параметр, с помощью которого можно выбирать, какой из показателей важнее - относительная взаимная связность или относительное взаимное сходство, а [math]t[/math] - параметр, показывающий самый нижний уровень сходства кластеров, при котором их можно слить.
• Если на какой-то итерации цикла ни одна пара кластеров не была слита, то завершить цикл.

1.3 Вычислительное ядро алгоритма

Из математического описания алгоритма следует, что вычислительное ядро алгоритма сосредоточено в вычислении относительной взаимной связности и относительного взаимного сходства каждой пары кластеров на каждой итерации алгоритма.

[math]RI(C_i, C_j) = \frac{|EC(C_i,C_j)|}{\frac{|EC(C_i)| + |EC(C_j)|}{2}}[/math]

[math]RC(C_i, C_j) = \frac{\bar{S}_{EC(C_i,C_j)}}{\frac{|C_i|}{|C_i|+|C_j|}\bar{S}_{EC(C_i)} + \frac{|C_j|}{|C_i|+|C_j|}\bar{S}_{EC(C_j)}}[/math]

1.4 Макроструктура алгоритма

В первой части первого этапа алгоритма применяется алгоритм построения графа методом k ближайших соседей.

Во второй части первого этапа алгоритма при разбиении кластера на два подкластера применяется алгоритм пакета METIS от Karypis Lab.

В виде макроопераций представлены вычисления относительной взаимной связности и относительного взимного сходства кластеров.

1.5 Схема реализации последовательного алгоритма

Реализация последовательного алгоритма на псевдокоде выглядит следующим образом:

 // параметры
 // число ближайших соседей в первой фазе алгоритма
 int k;
 // минимальный относительный размер каждого из начальных кластеров
 double MINSIZE;
 // параметры, определяющий, что важнее в определении похожести
 // двух кластеров - относительная взаимосвязанность
 // или относительная близость
 int alpha;
 // порог, определяющий минимальную похожесть кластеров, необходимую
 // для их слияния
 int threshold;
 int n = number_of_vertices;
 double graph_matrix[n][n] = {0};
 // фаза 1 - для каждой вершины найдем k ближайших к ней и соединим 
 // получившиеся наборы ребрами
 for (int i = 0; i < n; i++) {
 	double k_nearest_indices[k] = findKNearest(i);
 	for (int near_ind = 0; near_ind < k; near_ind++) {
 		connect(i, near_ind);
 	}
 }
 // фаза 2 - осуществление начального разбиения на кластеры
 Cluster initial_clusters[] = all(graph_matrix);
 while (1) {
 	Cluster greatest = getGreatestCluster(initial_clusters);
 	if (greatest.size() / n < MINSIZE) {
 		break;
 	} then {
 		Cluster c1;
 		Cluster c2;
 		(c1, c2) = greatest.splitClusterIntoTwo();
 		initial_clusters.remove(greatest);
 		initial_clusters.push_back(c1);
 		initial_clusters.push_back(c2);
 	}
 }
 // фаза 3 - выполним слияние кластеров
 Cluster current_clusters[] = initial_clusters;
 bool already_merged[] = {false};
 Cluster clusters_merged[];
 // возвращает логическую переменную, показывающую,
 // произошло ли слияние или нет
 bool merge(int i, int j) {
 	if (already_merged(i) || already_merged(j)) {
 		return false;
 	}
 
 	Cluster c1 = current_clusters[i];
 	Cluster c2 = current_clusters[j];
 	
 	double RI = calcRI(c1, c2);
 	double RC = calcRC(c1, c2);
 	double similarity = pow(RI, alpha) * RC;
 	if (similarity > threshold) {
 		already_merged(i) == true;
 		already_merged(j) == true;
 		
 		Cluster merged = connect_clusters(i, j);
 		clusters_merged.push_back(merged);
 		
 		return true;
 	}
 	return false;
 }
 // слияние
 while (1) {
 	bool some_merging_happened = false;
 	for (each pair (i, j) in current_clusters) {
 		some_merging_happened ||= merge(i, j);
 	}
 	if (some_merging_happened) {
 		current_clusters = clusters_merged;
 		clusters_merged = null;
 		
 		already_merged = {false};
 	} else {
 		break;
 	}
 }
 // результат
 print current_clusters

1.6 Последовательная сложность алгоритма

Для расчета последовательной сложности алгоритма необходимо рассчитать сложность каждого из его этапов. Везде далее будем считать, что [math]n[/math] – размер входной выборки данных (иначе говоря, число точек). Также через [math]m[/math] обозначим число начальных кластеров, появившихся после этапа 2 алгоритма, и для простоты анализа будем считать, что размер каждого из кластеров равен [math]\frac{n}{m}[/math].

• Построение графа [math]k[/math]-ближайших соседей. Для нахождения [math]k[/math] ближайших соседей одной фиксированной вершины в общем случае требуется [math]O(n)[/math] шагов, следовательно, для всего этапа требуется [math]O(n^2)[/math] шагов.
• Построение начального набора кластеров. Пусть дан граф [math]G=(V,E)[/math]. Один шаг алгоритма – разбиение кластера максимального размера на 2 подкластера – может быть выполнен за [math]O(|V|+|E|)[/math] шагов. Так как мы исходной точкой для данного этапа является граф [math]k[/math]-ближайших соседей, [math]|E|=O(|V|)[/math], следовательно, шаг может быть выполнен за [math]O(|V|)=O(n)[/math] шагов. Суммарная же сложность всего этапа будет равна [math]O(n log(\frac{n}{m}))=O(n log(n))[/math], так как в итоге получаются [math]m[/math] кластеров.
• Сложность третьего этапа зависит от сложности вычисления относительной взаимной связанности и относительного взаимного сходства. Эти две операции вычисляются с помощью нахождения минимального разреза соответствующего кластера, что означает, что их сложность пропорциональна числу элементов в каждом кластере. В частности, время, необходимое на разделение каждого из изначальных m кластеров, равно [math]O(\frac{n}{m})[/math], а суммарно необходимо [math]O(n)[/math] времени. Далее, необходимо сделать [math]m - 1[/math] объединений [math]m[/math] изначальных кластеров, отсюда, суммарная сложность вычислений похожести равна [math]O(nm)[/math]. Суммарное время, требуемое для нахождение наиболее похожей пары кластеров, равно [math]O(m^2 log(m))[/math].
• Таким образом, итоговая сложность алгоритма равна [math]O(n^2+nm+n log n + m^2 log(m))[/math].

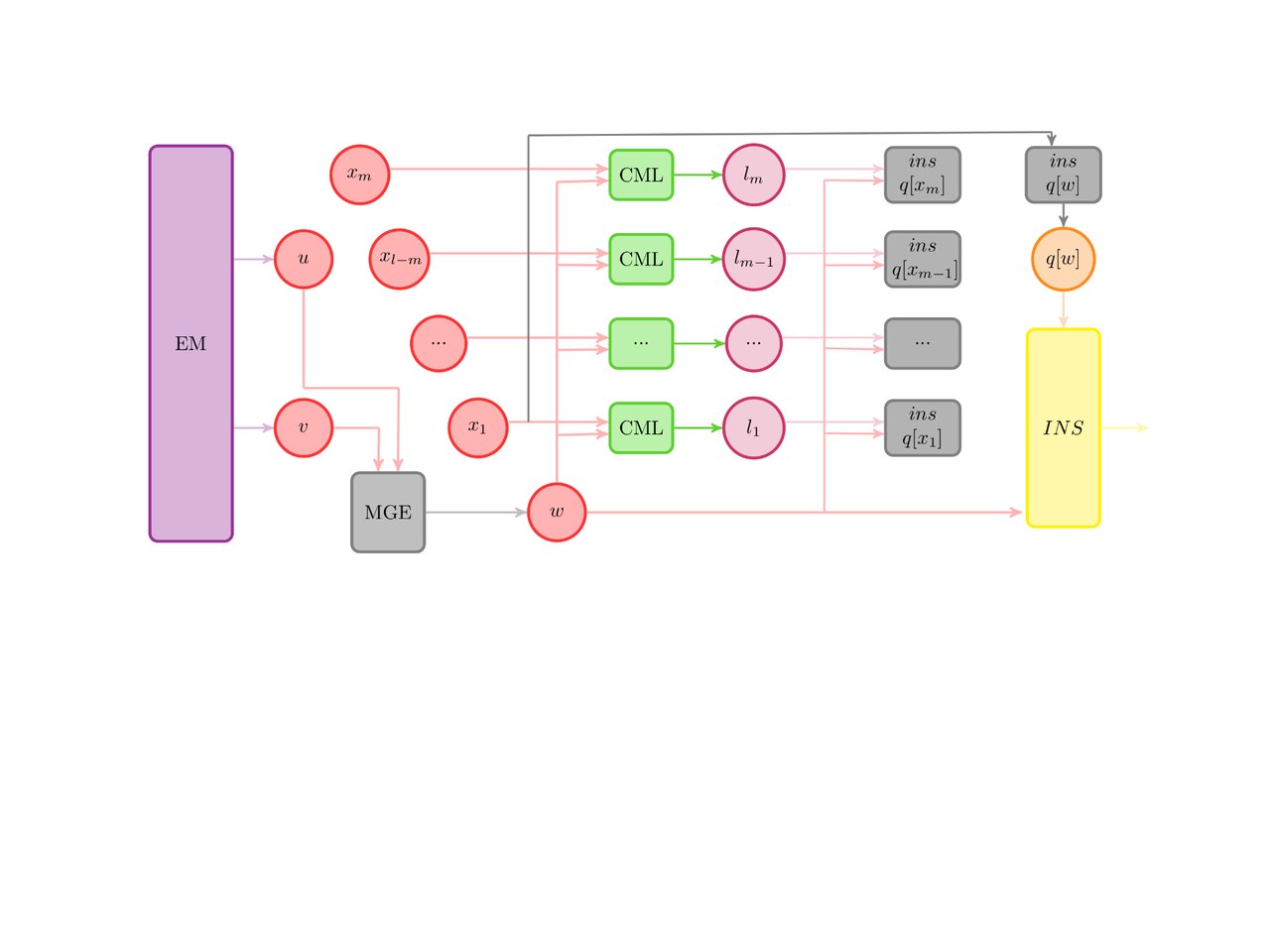
1.7 Информационный граф

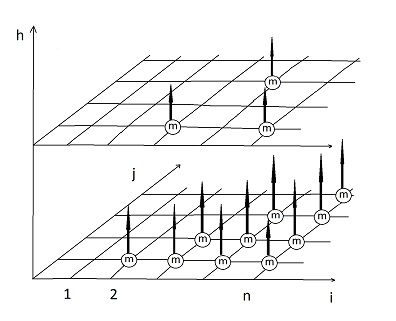
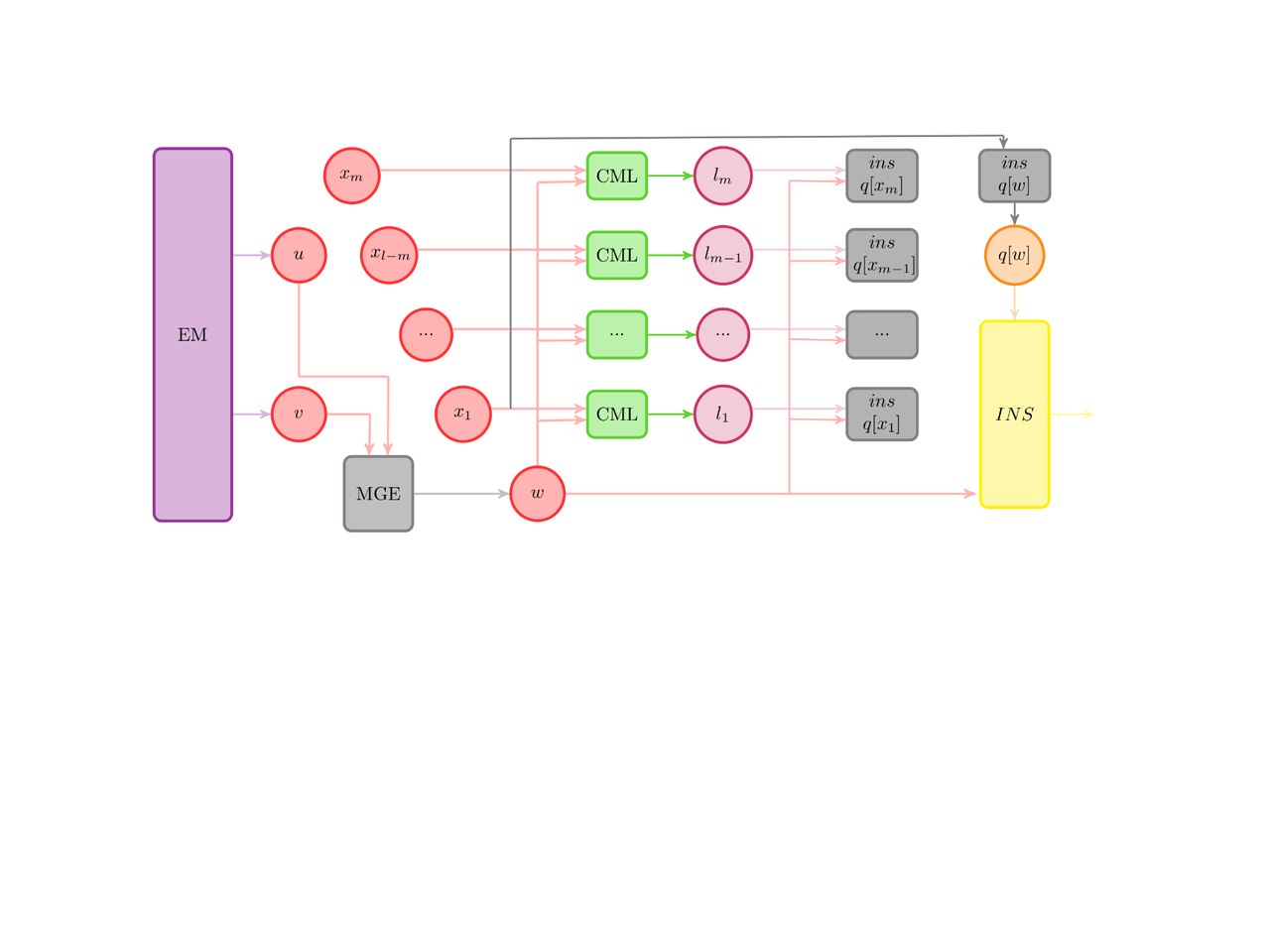
Покажем информационный граф основной части алгоритма. Он представляет собой трехмерный набор точек-итераций главного цикла. Плоскость [math](i,j)[/math] являет собой последовательную проверку на слияние пары кластеров с номерами [math]i[/math] и [math]j[/math]. Ось [math]h[/math] являет собой номер текущего набора кластеров, иначе говоря – номер итерации главного цикла. Операции слияния обозначены кружком с буквой “m” внутри.

Из графа алгоритма видно, что переходить к следующей итерации главного цикла можно лишь тогда, когда будет завершена предыдущая (дуги-зависимости идут от операций слияния строго вверх).

1.8 Ресурс параллелизма алгоритма

Как видно из графа алгоритма, операции слияния, находящиеся на одной итерации-плоскости главного цикла, не зависят друг от друга, и, следовательно, могут быть выполнены параллельно. Исходя из этого, предлагается следующая схема выполнения параллельного выполнения: каждая операция слияния на одной итерации главного цикла вызывается асинхронно, а в конце одной итерации главного цикла происходит ожидание окончания работы всех операций и подготовка к следующей итерации.

Стоит заметить, что создание числа параллельных потоков, равного текущему количеству кластеров, вряд ли можно считать реальной задачей. Поэтому будем считать, что каждый параллельный поток вычисляет ровно один столбец матрицы-плоскости информационного графа, что означает, что параллельная сложность выполнения одной итерации алгоритма равна [math]O(n)[/math]. Высота полученного графа (то есть, число позиций по вертикальной оси) будет равна [math]O(log(n))[/math], так как на каждом шаге цикла число кластеров уменьшается в среднем в 2 раза.

1.9 Входные и выходные данные алгоритма

Входные данные: массив [math]n[/math] точек произвольной размерности.

Выходные данные: [math]n[/math] чисел [math]q_1, q_2, ..., q_n[/math], где [math]q_i[/math] - целое число, соответствующее кластеру [math]i[/math]-й точки.

1.10 Свойства алгоритма

Алгоритм делится на три части, которые выполняются последовательно и отдельно друг от друга. В пределах каждой части возможна параллельная реализация.

Детерминированность: Важной особенностью данного алгоритма является его недетерминированность. Несмотря на то, что первая часть первого этапа детерминирована, остальные две части выполняются итеративно и останавливаются по достижении заданной точности.

2 ЧАСТЬ. Программная реализация алгоритма

2.2 Существующие реализации алгоритма

Существующая реализация алгоритма CHAMELEON есть в составе пакета CLUTO от авторов алгоритма. Подробнее можно посмотреть по ссылке [4].

3 Литература

[1] CHAMELEON: A Hierarchical Clustering Algorithm Using Dynamic Modeling George Karypis Eui-Hong (Sam) Han Vipin Kumar Department of Computer Science and Engineering University of Minnesota 4-192 EECS Bldg., 200 Union St. SE Minneapolis, MN 55455, USA Technical Report #99–007 {karypis,han,kumar}@cs.umn.edu

[2] International Journal of Computer Applications (0975 – 8887) Volume 79 – No8, October 2013 11 Parallel Algorithm for the Chameleon Clustering Algorithm using Dynamic Modeling

[3] ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ КАЧЕСТВА КЛАСТЕРИЗАЦИИ РАЗНООБРАЗНЫХ НАБОРОВ ДАННЫХ С ПОМОЩЬЮ МОДИФИЦИРОВАННОГО АЛГОРИТМА ХАМЕЛЕОН © Т. Б. Шатовская, А. А. Заремская

[4] Data Clustering Software CLUTO - Software for Clustering High-Dimensional Datasets