Участник:Kisel dv/DNS алгоритм умножения матриц

Автор: Д.В.Кисель

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

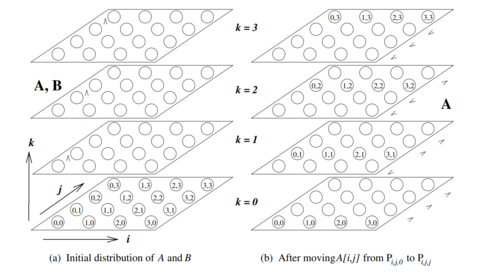
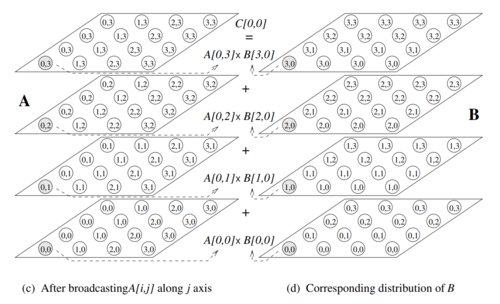
Алгоритм DNS(Dekel, Nassimi, Sahni - назван по фамилиям создателей) является одним из блочных алгоритмов решения задачи $C = AB$  перемножения двух матриц. Для данного алгоритма мы не используем какие-либо свойства матриц $A$  и $B$ . DNS основан на блочном разделении данных, его преимуществом является временная сложность $O(log(n))$  при вычислительной сложности $O(\frac{n^3}{log(n)})$ . Достигается это за счет 3d-секционирования(англ. partitioning), в отличие от альтернатив, использующих 2d-секционирование(например, алгоритм Кэннона). Тем самым, алгоритм DNS представим в виде куба, где матрицы $A$ , $B$  и матрица $C$  ортогональны друг другу. Далее данное описание будет рассмотрено подробнее.

1.2 Математическое описание алгоритма

Исходные данные: матрицы $A$  и $B$  с блоками $A_{ij}$  и $B_{ij}$ , соответственно.

Вычисляемые данные: матрица $C$  с блоками $C_{ij}$ 

Используемые формулы:

$C_{ij} = \sum_{k=0}^{m-1} A_{ik} B_{kj} \quad i \in [0, m-1], \quad j \in [0, m-1]$ , где $m \times m$  - количество блоков матрицы.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро перемножения матриц методом DNS состоит из вычислений всех элементов блоков матрицы-результата: процедур вычислений умножения блоков матрицы $A$  на блоки матрицы $B$ 

$\sum_{k=0}^{m-1} A_{ik} B_{kj} \quad i \in [0, m-1], \quad i \in [0, m-1]$ 

1.4 Макроструктура алгоритма

В алгоритме используется:

$\cdot$  произведение блоков матриц $A$  и $B$ 

$\sum_{k=1}^{n} a_{ik} b_{kj}$ 

1.5 Схема реализации последовательного алгоритма

Обнулим матрицу $C$ , предназначенную для записи полученного результата произведения $C = AB$ . Рассмотрим блоки матриц: $A_{ij}, B_{ij}, C_{ij}$ . В цикле выполним последовательное умножение блоков матриц операндов и суммирование результатов.

$C_{ij} = \sum_{k=0}^{m-1} A_{ik} B_{kj} \quad i \in [0, m-1], \quad j \in [0, m-1]$ 

В результате получаем матрицу $C$ , равную произведению матриц $A$  и $B$ .

1.6 Последовательная сложность алгоритма

Рассматриваем матрицы размером $n \times n$ , разбитые на $m \times m$  блоков размера $\frac{n}{m}$ .

Для умножение данных матриц в последовательном варианте требуется по $n^3$  умножений и сложений.

При классификации по последовательной сложности, таким образом, алгоритм умножения матриц относится к алгоритмам с кубической сложностью.

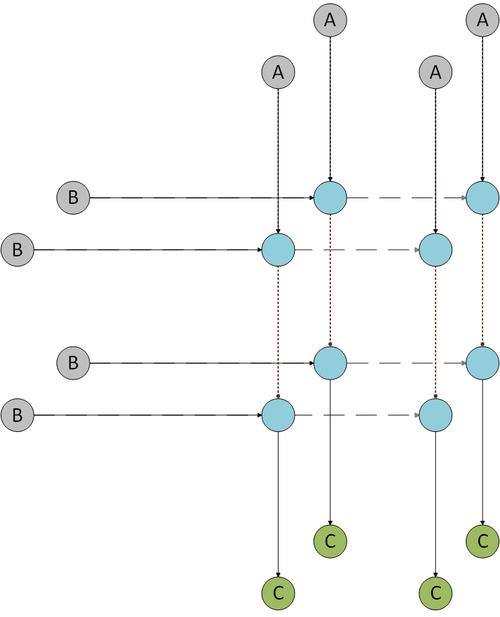
1.7 Информационный граф

Серым на графе помечен этап, в котором происходит считывание матриц $A$ и $B$ и их запись в "смежные грани куба".

Далее как бы проецируем каждый блок матрицы на каждую плоскость куба из процессов(на каждую плоскость, параллельную рассматриваемой матрице, см.рисунок выше), таким образом в каждом из них будет выполняться свое умножение уникальной комбинации блоков("синий" этап).

Зеленым обозначен этап суммирования и вывода результата - матрицы $C$.

1.8 Ресурс параллелизма алгоритма

$\cdot$  Рассмотрим $m^3$  процессов, доступных для умножения двух матриц размером $n \times n$ , разбитых на $m \times m$  блоков. Представим их в виде трехмерного массива $m \times m \times m$ .

$\cdot$  Процессы именованы согласно их расположению в массиве, соответственно, вычисление произведения $A_{ik}B_{kj}$  присвоено процессу с координатами $[i, j, k] (0 \leq i,j,k \lt m)$ .

$\cdot$  После того, как каждый процесс завершил умножение, результаты процессов $[i, j, 0], [i, j, 1], ..., [i, j, m-1]$  суммируются в $C_{ij}$ . Суммирование всех $C_{ij}$  может выполняться одновременно за $log(m)$  шагов.

1.9 Входные и выходные данные алгоритма

Входные данные: матрица $A$ (элементы $a_{ij}$), матрица $B$ (элементы $b_{ij}$)).

Объём входных данных: $2n^2$

Выходные данные: матрица $C$ (элементы $c_{ij}$).

Объём выходных данных: $n^2$

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

2.4.1 Масштабируемость алгоритма

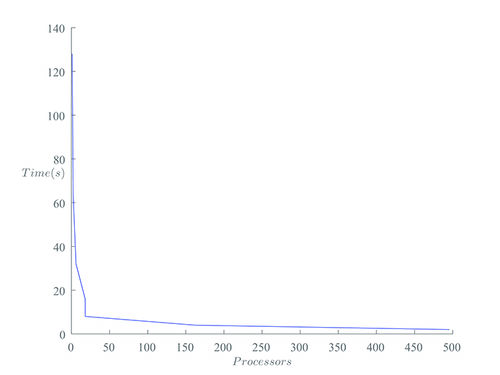
Рассматривались квадратные матрицы размерностью $N$, где $500\leqslant N \leqslant 2000$, а число процессов изменялось от $2$ до $128$. Для примера посмотрим как изменялось время выполнения программы в зависимости от числа процессов (здесь берутся матрицы размера $N = 2000$)

Размер блоков, на которые разбивается матрица, выбирается по оптимальному принципу: целая часть от $\frac{N}{q^{\frac{1}{3}}}$, где $N, q$, соответственно, размер матрицы и количество процессов.

Число процессов	Время (с)
128	0.976
64	2.245
32	6.012
16	18.012
8	18.153
4	162.214

Приблизительно одинаковые результаты по времени на количестве процессов, равном 8 и 16, обусловлены равным числом по факту используемых процессов в программе, поскольку деление в данных двух случаях будет происходить на равные блоки(выше указана оптимальная формула для количества блоков).

Проиллюстрируем данные графиком:

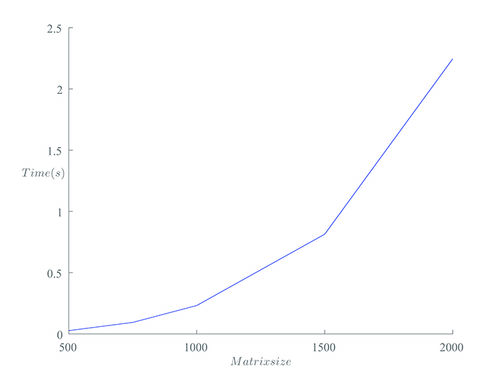
А теперь посмотрим на зависимость времени выполнения программы от размера матриц. Число процессов зафиксируем равным $64$.

Размер матриц	Время (с)
2000	2.245
1500	0.814
1000	0.232
750	0.094
500	0.027

Проиллюстрируем данные графиком:

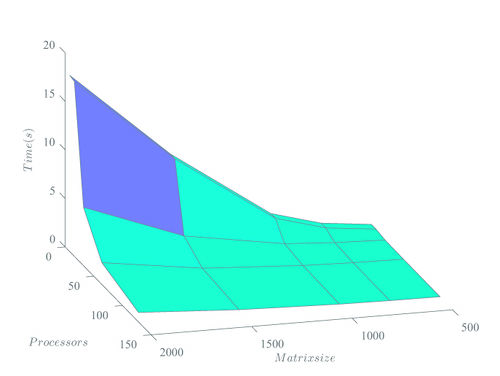
3d-график:

Очевидно, что система хорошо масштабируема.

2.4.2 Характеристики программно-аппаратной среды

Все вычисления были произведены на суперкомпьютере "Ломоносов".

Для компиляции был использован компилятор языка C++ GNU 4.4.6, реализация MPI: Intel MPI 4.0.3. При компиляции использована опция -lm (подключение библиотеки math).

Вычисления производились в очереди test. Ограничений на лимит времени на узел наложено не было.

2.7 Существующие реализации алгоритма

DNS алгоритм не очень распространен в Интернете, сравнительно просто отыскать лишь текстовое описание данного способа умножения матриц. Чуть более трудной, однако выполнимой задачей будет нахождение его реализации, например, на github.