Участник:Kiseliov/Метод регуляризации Тихонова

Автор: Киселёв Е. И.

1 ЧАСТЬ. Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Метод регуляризации Тихонова заключается в следующем:

Нам дано некоторое искажённое изображение (в нашем случае мы рассматриваем статические аберрации). Фактически, некоторое изображение искажается при помощи свёртки с так называемым ядром. То есть, мы имеем уравнение Фредгольма первого рода типа свертки вида:

$K \circledast z =\textstyle\int\limits_{-\infty}^{\infty}\textstyle\int\limits_{-\infty}^{\infty}K(x_1-s_1,x_2-s_2 )z(s_1,s_2 )ds_1\,ds_2 = u(x_1,x_2 ), -\infty\lt x_1,x_2\lt \infty$

Здесь $K(x_1,x_2 )∈L_2 (\mathbb{R}^2)$ – аппаратная функция прибора (ядро), $u(x_1,x_2 )∈L_2 (\mathbb{R}^2)$ – искаженное изображение, а $z(x_1,x_2 )$ – искомое реконструируемое изображение.

Наша задача - восстановить исходное изображение, зная параметры ядра. Метод регуляризации Тихонова говорит о том, что решение имеет вид:

$z(x_1 ,x_2 ) = \frac{1}{4\pi^2}\textstyle\int\limits_{-\infty}^{\infty}\textstyle\int\limits_{-\infty}^{\infty}\frac{\bar K (-\omega_1,-\omega_2)\bar u (\omega_1,\omega_2)}{|\bar K (\omega_1,\omega_2 )|^2+\alpha M(\omega_1,\omega_2)}e^{i(\omega_1x_1 + \omega_2x_2)}d\omega_1\,d\omega_2$

Здесь $\bar K (x_1,x_2 )$ – спектр ядра, $\bar u (x_1,x_2 )$ – спектр искаженного изображения, а $M(\omega_1,\omega_2)$ – заданная четная функция, обладающая следующими свойствами:

1. $M(\omega_1,\omega_2)$ кусочно-непрерывна в любой конечной области
2. $M(\omega_1,\omega_2)$ неотрицательна: $M(0,0)\ge0$ и $M(\omega_1,\omega_2)\gt 0$ при $\omega_1,\omega_2\neq0$
3. для достаточно больших $|\omega_1|,|\omega_2| \Rightarrow M(\omega_1,\omega_2)\ge C\gt 0$
4. для $\forall \alpha \gt 0 \Rightarrow \frac{\bar K (-\omega_1,-\omega_2)}{|\bar K (\omega_1,\omega_2 )|^2+\alpha M(\omega_1,\omega_2)}∈L_2 (\mathbb{R}^2)$

1.2 Математическое описание алгоритма

Пусть нам даны спектры искажённого изображения $\bar u_{ij}$ и ядра $\bar K_{ij}$ - это квадратные матрицы, состоящие из комплексных чисел, размера $N\times N$. Тогда спектр исходного изображения в позиции $(i, j)$ находится по формуле:

$\bar z_{ij} =\frac{(\bar K_{ij})^*\bar u_{ij} (\vartriangle x)^2}{\bigl|\bar K_{ij}\bigl|^2(\vartriangle x)^4+\alpha \bigl(\bigl(\frac{\pi}{2R}\bigl)^2(i^2+j^2)\bigl)^r}$

Здесь $\vartriangle x=\frac{4R}{N}$, где R - один из параметров ядра (известная, наперёд заданная величина).$(\bar K_{ij})^*$ - сопряжение спектра ядра. $\alpha$ и $r$ - параметры метода.

В реализации будем считать $\alpha = 0.5$ и $r = 1$ (наиболее подходящие параметры в нашем случае).

1.3 Вычислительное ядро алгоритма

В данном методе вычислительным ядром являются вычисления по формуле из пункта 1.2 в позиции $(i, j)$, поскольку формула применяется к позиции $(i, j)$ независимо от других точек.

Вычислительная сложность формулы - 3 умножения в числителе, 9 умножений, 2 сложения в знаменателе и одно общее деление (возведение в степень не считаем, так как положили $r = 1$). Итого, 15 операций. Формулы применяется независимо в каждой точке $(i, j)$ $\Rightarrow$ вычислительная сложность ядра алгоритма - 15 операций.

1.4 Макроструктура алгоритма

Макроструктура алгоритма представляет собой проход по всем точкам (i, j) и вычисление (i, j) позиции результирующей матрицы по формуле, указанной в пункте 1.2.

1.5 Схема реализации последовательного алгоритма

Реализация указанного алгоритма на псевдокоде в стиле C:

tikhonov_regularization(N, *image, *kernel, R, alpha, r, *restored)
{
    // ДельтаX в формуле (логично посчитать эти значения единожды)
    delta_x = (4 * R) / N;
    delta_x_pow2 = delta_x * delta_x;
    delta_x_pow4 = delta_x_pow2 * delta_x_pow2;

    // Это выражение - константа, и его логично посчитать заранее. CONSTANT_PI - число пи
    constant = (CONSTANT_PI / (2 * R)) * (CONSTANT_PI / (2 * R));

    // Цикл по позициям (i, j)
    for (i = 0; i < N; i++)
        for (j = 0; j < N; j++)
        {
            // Предполагается, что матрицы хранятся в виде 1D массива, поэтому нужно вычислить правильный индекс
            index = i * N + j;

            // Мы сдвигаем центр системы координат в центр изображения
            m = i - N / 2;
            n = N / 2 - j;
            
            // Вычисление формулы. Предполагается, что pow возводит число в степень, conj возвращает сопряжённое комплексное число,
            // .real() и .imag() - получение действительной или мнимой частей комплексного числа соответственно.
            upper_part = conj(kernel[index]) * image[index] * delta_x_pow2;
            kernel_squared_module = kernel[index].real() * kernel[index].real() + kernel[index].imag() * kernel[index].imag();
            down_part1 = kernel_squared_module * delta_x_pow4;
            m_pow2 = m * m;
            n_pow2 = n * n;
            down_part2 = alpha * pow(constant * (m_pow2 + n_pow2), r);
            down_part = down_part1 + down_part2;
            restored[index] = upper_part / down_part;
        }
}

1.6 Последовательная сложность алгоритма

В пункте 1.3 мы получили, что число операций, необходимых для вычисления формулы, равно $15$. Всего формула будет применена $N^2$ раз. Итого, в последовательном варианте сложность составит $15 * N^2$ операций.

1.7 Информационный граф

Рисунок 1. Информационный граф метода регуляризации Тихонова. Вершины означают применение формулы из пункта 2 к $(i, j)$ позиции входа для получения $(i, j)$ позиции выхода. Рёбра в графе отсутствуют в связи с отсутствием связей по данным.

1.8 Ресурс параллелизма алгоритма

Поскольку в каждой позиции $(i, j)$ вычисления производятся независимо, то ресурс параллелизма будет равен размеру матриц, то есть $N^2$.

1.9 Входные и выходные данные алгоритма

Входные данные: Две матрицы размера $N\times N$ - спектр искажённого изображения и спектр ядра свёртки. Обычно дано искажённое изображение (от которого берётся преобразование Фурье). Мы считаем параметры ядра известными. Оно генерируется, и затем от него берётся преобразование Фурье (получается спектр).

Выходные данные: Матрица размера $N\times N$ - спектр исходного изображения. Спектр можно преобразовать в изображение с помощью обратного преобразования Фурье.

2 ЧАСТЬ. Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Все запуски программы проводились на с/к Ломоносов 2. Для распараллеливания использовалась технология OpenMP.

Характеристики системы

Характеристика	Значение
Пиковая производительность	5,505 Пфлопс
Производительность на тесте Linpack	2,478 Пфлопс
Число вычислительных узлов	1 730
Основной тип процессора	Intel Haswell-EP E5-2697v3, 2.6 GHz, 14 cores
Тип ускорителя	NVidia Tesla K40M
Общее число ядер	64 384
Оперативная память на узел	64 GB
Проектная мощность	10 МВт
Операционная система	CentOS 7

Конфигурация системы в разделе compute (в котором производились запуски программы):

1487 узлов со следующими характеристиками

Характеристика	Значение
Объём памяти на GPU	11.56 GB
Центральный процессор	Intel Haswell-EP E5-2697v3, 2.6 GHz, 14 cores
Графический ускоритель	NVidia Tesla K40M
ОЗУ	64 GB

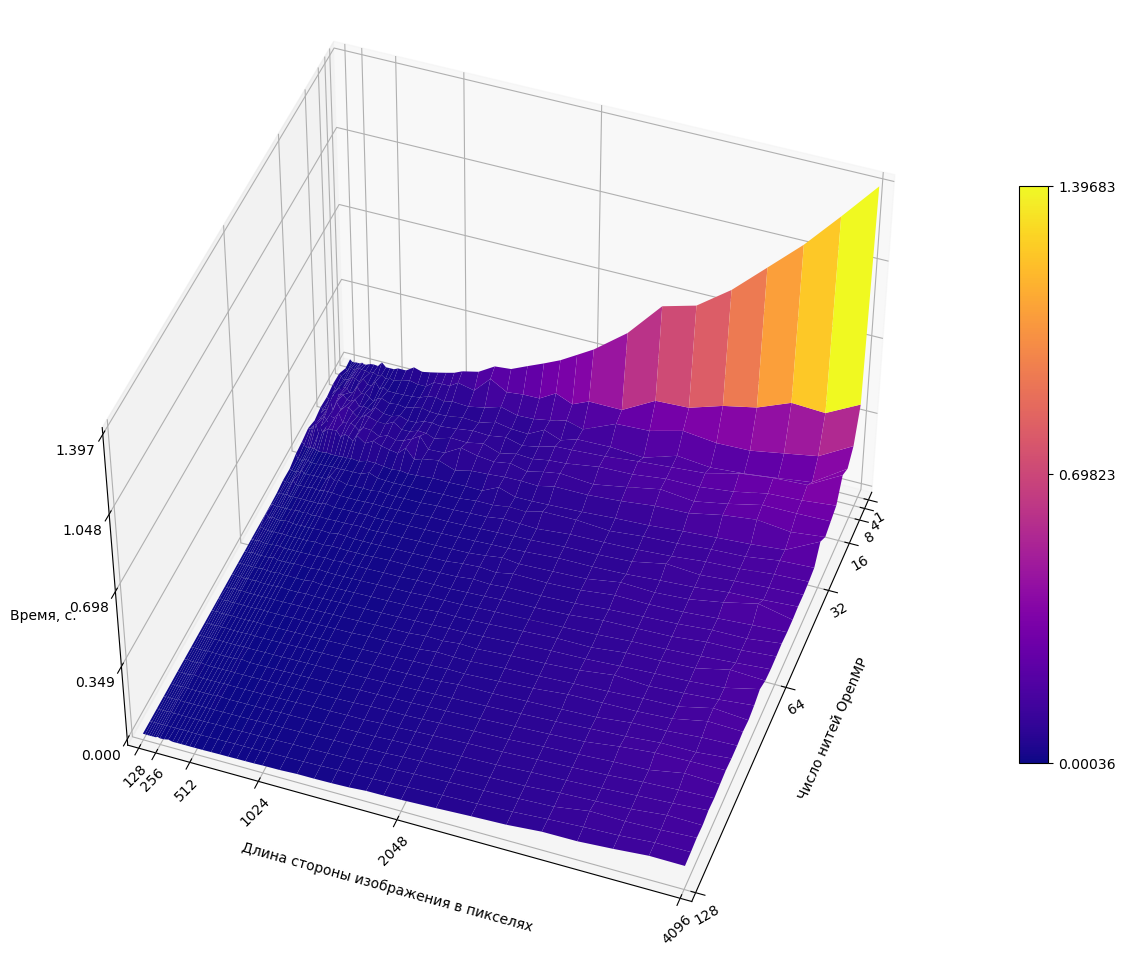
Перейдём к графику времени работы алгоритма. На графике по оси Ox, Oy откладывается длина одной стороны изображения в пикселях (т.е. это - число $N$, если всё изображение - матрица размера $N\times N$) и количество нитей OpenMP (нити запускаются параллельно, если доступно необходимое количество ресурсов). По оси Oz откладывается время работы в секундах для каждой точки $(x, y)$. Временем работы здесь является время работы функции, применяющей метод регуляризации Тихонова к изображению и ядру и заполняющей выходную матрицу. Время чтения/записи файлов, а также время выполнения прочих служебных функций не учитывалось. Количество нитей задаётся следующей последовательностью: $1, 4, 8, 12, 16, 20, ..., 128$. А длина стороны изображения в пикселях задаётся такой последовательностью: $128, 128+16, ..., 256, 256+32, ..., 4096$

2.7 Существующие реализации алгоритма

Автору такие не известны. Поиск в открытых источниках результата не дал.

3 Литература

• Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. – М.: Наука, 1979.
• Тихонов А.Н., Гончарский А.В., Степанов В.В., Ягола А.Г. Численные методы решения некорректных задач. – М.: Наука, 1990.
• Гудмен Дж. Введение в фурье‐оптику. – М.: Мир, 1970. 364 с.