Участник:Matfu/Решающие деревья

Обучение деревьев решений - это подход к обучению с учителем, используемый в статистике, интеллектуальном анализе данных и машинном обучении. В этом формализме дерево классификации или регрессии используются в качестве предсказательной модели для вывода заключений о наборе наблюдений.

Деревья моделей, в которых целевая переменная может принимать дискретный набор значений, называются деревьями классификации; в этих структурах дерева листья представляют метки классов, а ветви представляют конъюнкции признаков, которые приводят к этим меткам классов. Деревья решений, в которых целевая переменная может принимать непрерывные значения (как правило, вещественные числа), называются деревьями регрессии. В более общем смысле понятие регрессионного дерева можно расширить на любые объекты, оснащенные попарными различиями, такие как категориальные последовательности.

Деревья решений являются одним из самых популярных алгоритмов машинного обучения благодаря их понятности и простоте.

Решающие деревья хорошо описывают процесс принятия решения во многих ситуациях. Например, когда клиент приходит в банк и просит выдать ему кредит, то сотрудник банка начинает проверять условия:

1. Какой возраст у клиента? Если меньше 18, то отказываем в кредите, иначе продолжаем.
2. Какая зарплата у клиента? Если меньше 50 тысяч рублей, то переходим к шагу 3, иначе к шагу 4.
3. Какой стаж у клиента? Если меньше 10 лет, то не выдаем кредит, иначе выдаем.
4. Есть ли у клиента другие кредиты? Если есть, то отказываем, иначе выдаем.

Такой алгоритм, как и многие другие, хорошо описывается решающим деревом.

Решающие деревья являются популярными алгоритмами машинного обучения из-за их интерпретируемости и простоты. Они также могут быть использованы в комбинации с другими алгоритмами, такими как случайный лес или градиентный бустинг, для улучшения производительности и устойчивости.

1 Свойства и структура алгоритмов

Определение решающего дерева. Рассмотрим бинарное дерево, в котором:

1. каждой внутренней вершине [math]v[/math] приписана функция (или предикат) [math]\beta_v: \mathbb{X} \to \{0, 1\}[/math];
2. каждой листовой вершине [math]v[/math] приписан прогноз [math]c_v \in Y[/math](в случае с классификацией листу также может быть приписан вектор вероятностей).

Рассмотрим теперь алгоритм [math]a(x)[/math], который стартует из корневой вершины [math]v_0[/math] и вычисляет значение функции [math]\beta_{v_0}[/math]. Если оно равно нулю, то алгоритм переходит в левую дочернюю вершину, иначе в правую, вычисляет значение предиката в новой вершине и делает переход или влево, или вправо. Процесс продолжается, пока не будет достигнута листовая вершина; алгоритм возвращает тот класс, который приписан этой вершине. Такой алгоритм называется бинарным решающим деревом.

На практике в большинстве случаев используются одномерные предикаты [math]\beta_v[/math], которые сравнивают значение одного из признаков с порогом:

[math] \begin{align} \beta_v(x; j, t) = [x_j \lt t]. \end{align} [/math]

Существуют и многомерные предикаты, например:

1. линейные [math]\beta_v(x) = [\langle w, x \rangle \lt t][/math];
2. метрические [math]\beta_v(x) = [\rho(x, x_v) \lt t][/math], где точка [math]x_v[/math] является одним из объектов выборки любой точкой признакового пространства.

Многомерные предикаты позволяют строить ещё более сложные разделяющие поверхности, но очень редко используются на практике, например, из-за того, что усиливают и без того выдающиеся способности деревьев к переобучению.

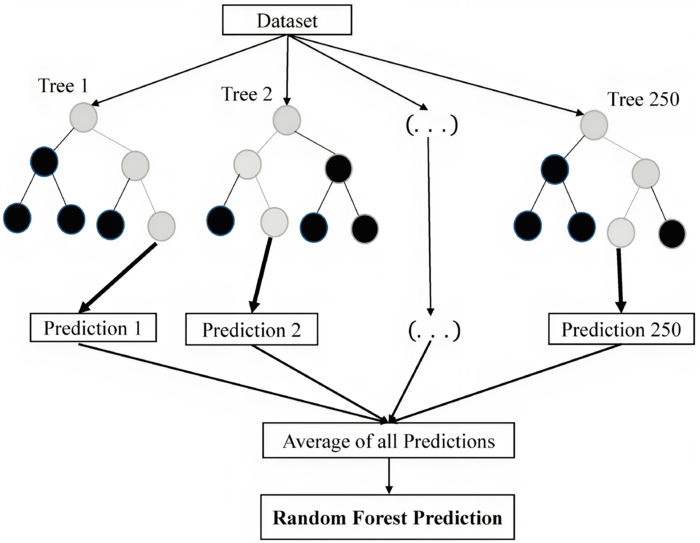
Метод случайного леса (англ. random forest) — алгоритм машинного обучения, предложенный Лео Брейманом и Адель Катлер, заключающийся в использовании ансамбля решающих деревьев. Алгоритм сочетает в себе две основные идеи: метод бэггинга Бреймана и метод случайных подпространств, предложенный Тин Кам Хо. Алгоритм применяется для задач классификации, регрессии и кластеризации. Основная идея заключается в использовании большого ансамбля решающих деревьев, каждое из которых само по себе даёт очень невысокое качество классификации, но за счёт их большого количества результат получается хорошим.

1.1 Общее описание алгоритма

Процесс построения решающего дерева состоит из нескольких этапов:

1. Инициализация: сначала создается корень дерева, представляющий весь набор данных.
2. Рекурсивное разделение: на каждом уровне дерева происходит разделение данных на основе определенного критерия. Критерии разделения могут основываться на различных метриках, таких как индекс Джини, энтропия или средняя квадратическая ошибка. Таким образом, выбирается пороговое значение наиболее значимого признака, по которому будет осуществляться разделение.
3. Прекращение разделения: когда процесс разделения достигает определенной глубины или не остается данных для дальнейшего разделения, остановка создания потомков и создание листа с меткой класса или прогнозируемым значением для регрессии.
4. Отсечение: в некоторых случаях, для борьбы с переобучением, может использоваться стратегия отсечения ветвей дерева. Это может включать удаление ветвей, не улучшающих характеристики дерева, создание деревьев с ограниченной глубиной или обрезание деревьев в соответствии с минимальным порогом улучшения критерия разделения.
5. Предсказание: после построения дерева оно может использоваться для предсказания меток классов или значений функции на новых данных. Для этого каждый объект пропускается через дерево по соответствующим условиям разделения, начиная с корня и заканчивая листом.

1.2 Математическое описание алгоритма

Для математического описания алгоритма построения решающего дерева рассмотрим жадный алгоритм для построения бинарного дерева. Пусть дана обучающая выборка [math]\mathbb{X} = (x_1, x_2, ..., x_n)[/math], необходимо найти оптимальное разделение на две части [math]R_1(j, t) = \{x | x_j \lt t\}[/math] и [math]R_2(j, t) = \{x | x_j \geq t\}[/math] с учетом заранее заданного критерия качества [math]Q(X, j, t)[/math]. После определения наилучших значений [math]j[/math] и [math]t[/math] создается корневой узел дерева, соответствующий предикату [math][x_j\lt t][/math]. Объекты разделяются на две части - некоторые попадают в левое поддерево, остальные – в правое. Этот процесс рекурсивно повторяется для каждого подмножества, и создаются дочерние узлы для корневого узла. В каждом узле проверяется выполнение условия остановки, и при его выполнении рекурсия прекращается, и узел объявляется листом. Когда дерево построено, каждому листу присваивается соответствующий ответ. В случае классификации это может быть класс с наибольшим количеством объектов в листе или вектор вероятностей (например, вероятность принадлежности к классу, равная доле объектов данного класса в листе). В случае регрессии это может быть среднее значение, медиана или другая функция от целевых переменных объектов в листе. Выбор определенной функции зависит от функционала качества, используемого в задаче.

Решающие деревья могут обрабатывать пропущенные значения - ситуации, когда для некоторых объектов неизвестны значения одного или нескольких признаков. Для этого необходимо изменить процедуру разделения выборки в узле, что возможно несколькими способами. После построения дерева, можно провести его стрижку (pruning) - удаление некоторых узлов с целью уменьшения сложности и повышения обобщающей способности.

Таким образом, конкретный метод построения дерева решений определяется:

1. Типом предикатов в узлах;
2. Критерием качества [math]Q(X, j, t)[/math];
3. Условием остановки;
4. Методом обработки пропущенных значений;
5. Методом стрижки.

При построении дерева необходимо задать функционал качества, на основе которого осуществляется разбиение выборки на каждом шаге. Пусть [math]R_m[/math] - множество объектов, попавших в вершину, разбиваемую на данном шаге, а [math]R_\ell[/math] и [math]R_r[/math] - объекты, попадающие в левое и правое поддерево соответственно при заданном предикате. Будем использовать функционалы следующего вида:

[math] \begin{align} Q(R_m, j, s) = I(R_m) - \frac{|R_\ell|}{|R_m|} I(R_\ell) - \frac{|R_r|}{|R_m|} I(R_r). \end{align} [/math]

Здесь [math]I(R)[/math] - критерий информативности(impurity criterion), который оценивает качество распределения целевой переменной среди объектов множества [math]R[/math]. Чем меньше разнообразие целевой переменной, тем меньше должно быть значение критерия информативности - и, соответственно, необходимо минимизировать его значение. Функционал качества [math]Q(R_m, j, s)[/math] необходимо при этом максимизировать.

1.2.1 Классификация

Пусть [math]p_k[/math] - доля объектов класса [math]k[/math] ([math]k \in \{1, \dots, K\}[/math]), попавших в вершину [math]R[/math]:

[math] \begin{align} p_{k} = \frac{1}{|R|} \sum_{(x_i, y_i) \in R} [y_i = k]. \end{align} [/math]

[math]k_*[/math] - класс, чьих представителей оказалось больше всего среди объектов, попавших в данную вершину: [math]k_* = \arg \max_k p_{k}[/math].

В качестве функции потерь рассмотрим индикатор ошибки:

[math] \begin{align} I(R) = \min_{c \in \mathbb{Y}} \frac{1}{|R|} \sum_{(x_i, y_i) \in R} [y_i \neq c]. \end{align} [/math]

Оптимальным предсказанием в данном критерии будет наиболее популярный класс [math]k_*[/math] - значит, критерий будет равен следующей доле ошибок:

[math] \begin{align} I(R) = \frac{1}{|R|} \sum_{(x_i, y_i) \in R} [y_i \neq k_*] = 1 - p_{k_*}. \end{align} [/math]

Данный критерий является достаточно грубым, поскольку учитывает частоту [math]p_{k_*}[/math] лишь одного класса.

Критерий Джини Рассмотрим ситуацию, в которой на каждом узле вместо единственного класса предоставляется распределение вероятностей для всех классов [math]c = (c_1, \dots, c_K)[/math], [math]\sum_{k = 1}^{K} c_k = 1[/math]. Если подставить эти вероятности в исходный критерий информативности Бриера(Brier score) и и выполнить ряд преобразований, то получим критерий Джини:

[math] \begin{align} I(R) = \sum_{k = 1}^{K} p_k (1 - p_k). \end{align} [/math]

Другой популярный критерий - энтропия:

[math] \begin{align} I(R) = - \sum_{k = 1}^{K} p_k \log p_k. \end{align} [/math]

1.2.2 Регрессия

Для регрессии используется среднеквадратическая ошибка:

[math] \begin{align} I(R) = \min_{c \in \mathbb{Y}} \frac{1}{|R|} \sum_{(x_i, y_i) \in R} (y_i - c)^2. \end{align} [/math]

Как известно, минимум в этом выражении будет достигаться на среднем значении целевой переменной. Значит, критерий можно переписать в следующем виде:

[math] \begin{align} I(R) = \frac{1}{|R|} \sum_{(x_i, y_i) \in R} \left( y_i - \frac{1}{|R|} \sum_{(x_j, y_j) \in R} y_j \right)^2. \end{align} [/math]

Функционал качества разделения выбирает предикат, который обеспечивает наибольшее улучшение качества:

[math] \begin{align} Q(R_m, j, s) = I(R_m) - \frac{|R_\ell|}{|R_m|} I(R_\ell) - \frac{|R_r|}{|R_m|} I(R_r). \end{align} [/math]

Повторяя процесс разделения до достижения критерия остановки (максимальная глубина, минимальное количество объектов в листе, минимальное улучшение качества и т.д.), получаем дерево [math]T[/math]. Затем для предсказания используем функцию [math]d_T(x)[/math], опуская объект от корня к листу с соответствующей меткой класса или прогнозируемым значением:

[math] \begin{align} d_T(x) = C_j \ \text{или} \ \widehat{y}. \end{align} [/math]

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма построения решающего дерева - это процесс рекурсивного разбиения данных на подмножества таким образом, чтобы каждое подмножество было однородным с точки зрения целевой переменной. То есть, в каждом подмножестве должны быть объекты только одного класса или значения целевой переменной. В качестве критериев разбиения могут использоваться различные меры неопределенности, такие как энтропия, Gini-индекс или коэффициент ошибок классификации. В данной реализации использовался алгоритм CART построения решающего дерева, в котором в качестве критерия расщепления выступает Gini-индекс.

Вычислительное ядро алгоритма случайного леса - это процесс создания множества решающих деревьев на основе подвыборок данных с возвращением и выбором случайного подмножества признаков для каждого разбиения в дереве. Каждое дерево строится независимо от других, а итоговое решение принимается путем голосования (для задач классификации) или усреднения (для задач регрессии) предсказаний отдельных деревьев.

1.4 Макроструктура алгоритма

Для построения случайного леса и последующего получения предсказания для решения задачи классификации и регрессии необходимо первоначально научиться строить решающее дерево. Макроструктура алгоритма построения CART включает следующие этапы:

1. Инициализация: создание корневого узла дерева на основе набора данных для обучения. Весь набор обучающих данных принадлежит корневому узлу.
2. Разделение узлов:
   1. Выбор подходящего атрибута и значения порога для разделения данных в узле на два подмножества (левое и правое).
   2. Разделение данных узла на два подмножества и создание для них дочерних узлов.
   3. Повторение пунктов 1 и 2 для каждого из новых узлов, пока не будет достигнут критерий останова или не будет достигнута максимальная глубина дерева.
3. Оценка критериев останова: оценка качества дерева на каждом этапе построения и определение момента останова, после которого дальнейшее расширение дерева не будет приводить к улучшению его качества.
4. Обработка ветвей и обрезка дерева: удаление некоторых из созданных ветвей и узлов дерева с целью сокращения его структуры и устранения переобучения. Обычно используется кросс-валидация для оценки качества усеченного дерева.
5. Завершение процесса: получение итоговой структуры дерева и применение его для решения задач классификации или регрессии на новых данных.

Макроструктура алгоритма случайного леса для задач классификации и регрессии включает следующие этапы:

1. Инициализация: выбор параметров ансамбля, таких как количество деревьев в лесу и максимальная глубина деревьев.
2. Построение ансамбля решающих деревьев:
   1. Создание бутстрапированной выборки (bootstrap sample) из исходного набора данных для обучения. Бутстрап-выборка содержит N объектов, выбранных случайным образом с возвращением (то есть один объект может быть выбран несколько раз, а некоторые объекты могут быть пропущены).
   2. Построение решающего дерева на основе полученной бутстрап-выборки с использованием метода CART. При выборе предиката для разделения узлов дерева, алгоритм случайного леса рассматривает только подмножество случайно выбранных предикатов для каждого узла (подпространство признаков).
   3. Повторение пунктов 1 и 2 заданное количество раз, чтобы построить необходимое число решающих деревьев.
3. Обучение: каждое дерево обучается на соответствующей ему бутстрап-выборке без обрезки или других процедур, устраняющих переобучение.
4. Предсказание:
   • Для задачи классификации: каждое дерево выполняет предсказание класса, а решение ансамбля принимается путем голосования большинства среди всех деревьев. Класс, получивший наибольшее число голосов от деревьев, принимается в качестве итогового предсказания.
   • Для задачи регрессии: каждое дерево выполняет предсказание числового значения, а решение ансамбля принимается путем усреднения предсказаний всех деревьев. Полученное среднее значение принимается в качестве итогового предсказания.
5. Оценка качества ансамбля: качество предсказания случайного леса оценивается посредством кросс-валидации, Out-of-Bag-оценки или других подходящих методов.

1.5 Схема реализации последовательного алгоритма

---

Процедура расщепления в алгоритме CART

---

1. Выбирается [math]k[/math]-ый признак [math]f_k[/math] c множеством значений [math]X^{(k)}[/math].
2. Определяется такое значение [math]x^{(k)}_0 \in X^{(k)}[/math] для всех признаков [math]f_k[/math], [math]k = 1, ..., m[/math], чтобы мера неоднородности [math]Gini_{split}(T)[/math] была минимальной, т.е. [math]x^{(k)}_0 = \arg \min_{f_k: x^{(k)} \in X^{(k)}} Gini_{split}(T, x^{(k)}).[/math]
3. Данная процедура выполняется рекурсивно для каждого полученного подмножества до тех пор, пока не будут достигнуты критерии остановки.

---

Алгоритм построения cлучайного леса

---

1. FOR [math] n = 1, \dots, N[/math]
   1. Сгенерировать выборку [math]\tilde X_n[/math] с помощью бутстрэпа
   2. Построить решающее дерево [math]b_n(x)[/math] по выборке [math]\tilde X_n[/math]:
      1. дерево строится, пока в каждом листе не окажется не более [math]n_{\min}[/math] объектов
      2. при каждом разбиении сначала выбирается [math]m[/math] случайных признаков из [math]p[/math], и оптимальное разделение ищется только среди них
2. Вернуть композицию [math]a_N(x) = \frac{1}{N} \sum_{n = 1}^{N} b_n(x)[/math]

1.6 Последовательная сложность алгоритма

Временная сложность построения CART (Classification and Regression Tree) решающего дерева составляет [math]O(N \times M \times \log(N))[/math], где [math]N[/math] - это количество объектов в данных, а [math]M[/math] - количество признаков.

Объяснение сложности:

1. В худшем случае, дерево может иметь глубину равную количеству объектов, что означает ([math]N-1[/math]) разбиение, которое должно быть выполнено.
2. На каждом шаге перебираются все признаки ([math]M[/math]) задаёт [math]M[/math] операций.
3. Для каждого признака запускается алгоритм поиска оптимального разбиения, которое занимает время [math]O(\log(N))[/math]. Это связано с тем, что алгоритм старается разделить данные на левое и правое поддерево таким образом, чтобы минимизировать функцию потерь. Затем алгоритм рекурсивно повторяется, пока не будет достигнут критерий останова.

---

Временная сложность построения случайного леса (Random Forest) зависит от количества решающих деревьев, которые необходимо построить ([math]n_{estimators}[/math]). В случае с CART временная сложность обучения одного решающего дерева составляет [math]O(N \times M \times \log(N))[/math].

Таким образом, временная сложность построения случайного леса будет равна [math]O(n_{estimators} \times N \times M \times \log(N))[/math]. Однако стоит отметить, что обучение деревьев в случайном лесе может выполняться параллельно, что сокращает время обучения модели. Также следует учесть, что случайный лес использует для построения деревьев подвыборку обучающей выборки или ее часть (параметр [math]max_{features}[/math]), что также может влиять на общую временную сложность алгоритма.

1.7 Информационный граф

Представленный информационный граф описывает параллельную версию построения случайного леса. На вход поступает набор данных, который используется в качестве обучающей выборки.  Каждое отдельное дерево соответствует своему потоку, все они выполняются независимо и параллельно. Распараллеливание в этом месте приводит к наибольшему уменьшению времени выполнения. Второй участок кода, в котором производится распараллеливание по потокам - поиск оптимального предиката для расщепления (на изображении выделено черным цветом). Здесь разные потоки оценивают разные подмножества кандидатов критериев расщепления. После того как каждое дерево было получено, итоговый ответ - усреднение ответов всех поддеревьев.

1.8 Ресурс параллелизма алгоритма

Параллелизм в программе реализован следующим образом:

Файл random_forest.cpp, отвечающий за функционал метода случайного леса, имеет распараллеленную версию randomForest.fit(), которая распределяет обучение отдельных деревьев по потокам. Именно здесь происходит наибольшая часть прироста производительности, поскольку теперь обучается параллельно num_threads деревьев вместо одного.

В файле decision_tree.cpp, содержащем функционал для построения решающих деревьев, реализован параллелизм в двух функциях predict() и findBestSplit(). Каждое дерево, являющееся частью случайного леса, имеет тип DecisionTree, поэтому здесь можно получить дополнительные выгоды от распараллеливания. Метод fit() для DecisionTree не распараллеливается, поскольку он выполняет рекурсивные вызовы для вычисления разбиений, и хотя мы могли бы распараллелить различные ветви процесса разбиения, а не жадно переходить слева направо, однако необходимые дополнительные накладные расходы, требующиеся для реализации последовательной версии данного алгоритма, быстро перевесят добавленную вычислительную мощность от распараллеливания. Метод predict() перебирает входные наблюдения, для того чтобы сделать прогноз для объекта, который является очевидным кандидатом для распараллеливания. Тонким местом является то, что объединение результирующих прогнозов должно выполняться в правильном порядке, что немного замедляет данный алгоритм.

Наконец, DecisionTree.findBestSplit() вызывается каждый раз, когда в дереве вычисляется новое расщепление. Он выполняет поиск среди потенциальных предикатов для использования в качестве критерия разбиения и оценивает все уникальные значения каждого из них, которые будут использоваться в качестве критериев. Это становится все более дорогостоящей задачей по мере роста набора данных. Данный метод также возможно распараллелить за счет того, что разные потоки оценивают разные подмножества пространства кандидатов критериев разделения, что заметно ускоряет время обучения, особенно в сочетании с распараллеленным randomForest.fit().

Для удобства обработки данных были реализованы пользовательские классы DataVector и DataFrame, однако реализация их параллелизма является весьма сложной задачей. В частности, OpenMP выполняет множество операций предварительного выделения, создания и удаления объектов, что требует очень тщательной реализации любых пользовательских классов и структур данных. Таким образом, при реализации распараллеливания с использованием прагм OpenMP в данном коде избегается использование пользовательских структур данных там, где это было возможно, вместо этого используя атомарные типы или стандартные объекты из пространства имен std. Само по себе это не было проблемой, но означало, что распараллеливание заключалось не просто в добавлении прагм, но требовало некоторого комплексного рефакторинга.

1.9 Входные и выходные данные алгоритма

Входные данные: набор табличных данных размера [math]N \times (d + 1)[/math] с целевой переменной для обучения ([math]N[/math] - количество объектов в обучающей выборке, [math]d[/math] - размерность признакового пространства), набор табличных данных размера [math]n \times d[/math] без целевой переменной для тестирования ([math]n[/math] - количество объектов в тестовой выборке)

Выходные данные: набор предсказаний размера [math]n[/math]

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Для тестирования был использован набор данных Sonar, Mines vs. Rocks предназначен для решения задачи классификации гидроакустических сигналов. Сонары (гидролокаторы) посылают звук высокой частоты в определенном направлении и получают отраженную звуковую волну. По характеристике этой волны можно сделать вывод, от чего именно она отразилась – от морской мины или же от подводного камня, скалы. Используемый для решения задачи набор данных был разработан сотрудником аэрокосмического технологического центра Полом Горманом в разгар холодной войны. Для получения данных металлический цилиндр и цилиндрическая горная порода, длиной около 1,5 метров, размещались на песчаном дне океана.

База данных о гидроакустических сигналах содержит 208 экземпляров и 60 атрибутов. Файл "sonar.mines" содержит 111 экземпляров, полученных путем отскакивания сигналов от мины под разными углами и при различных условиях. Файл "sonar.rocks" содержит 97 экземпляров, полученных от камней или скал в аналогичных условиях. Переданный сигнал гидролокатора представляет собой частотно-модулированный ЛЧМ, повышающийся по частоте. Каждый экземпляр представляет собой набор из 60 чисел в диапазоне от 0,0 до 1,0. Каждое число представляет энергию в пределах определенной полосы частот, полученной за определенный период времени. Метка, связанная с каждой записью, содержит букву «R» ("Rocks"), если объект представляет собой камень/скалу, и «M» ("Mines"), если это мина. Оба файла с представлением данных были интегрированы в один csv-файл "sonar.all-data.csv".

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

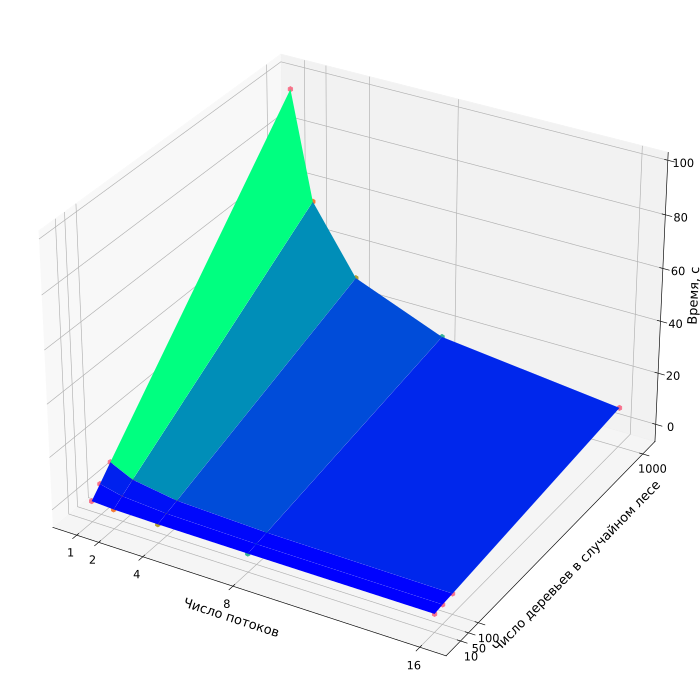
• число потоков [1, 2, 4, 8, 16];
• количество деревьев в случайном лесе [10, 50, 100, 10000].

На рис. 2 приведен график времени выполнения алгоритма в зависимости от изменяемых параметров запуска.

Рисунок 2. Время выполнения алгоритма в зависимости от числа потоков и количества деревьев

Отмечается значительный прирост скорости вычисления при переходе с последовательной на параллельную версию. Однако, увеличение числа вычислительных устройств не дает такого же сильного эффекта, так как накладные расходы на организацию параллельного выполнения быстро растут, превалируя над вычислениями. Таким образом, подтверждается предположение о том, что накладные расходы начинают сильно влиять на процесс вычислений.

2.7 Существующие реализации алгоритма

Деревья решений являются популярным алгоритмом машинного обучения, они реализованы во многих библиотеках, включая:

1. Scikit-learn (Python) - наиболее известная библиотека для машинного обучения в Python, которая включает различные модели деревьев решений, такие как DecisionTreeClassifier и DecisionTreeRegressor.

2. WEKA (Java) - популярная библиотека для машинного обучения и анализа данных, которая содержит несколько реализаций деревьев решений, например, J48 Algorithm for Decision Tree.

3. MATLAB - математический программный пакет, который также оснащен инструментами для создания деревьев решений, таких как fitсtree и fitrtree для классификации и регрессии соответственно.