Участник:Msindeeva/Алгоритм k средних

Алгоритм k средних

Автор статьи: Синдеева Мария, группа 416

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм k средних - это алгоритм кластерного анализа, используемый в Data Mining. Цель алгоритма - разделить $n$ наблюдений на $k$ кластеров, в которых каждое наблюдение принадлежит к кластеру с ближайшим центром, который служит прототипом всего кластера. Эта задача является NP-сложной, но существуют эффективные эвристические алгоритмы, быстро сходящиеся к локальному минимуму.

Алгоритм k средних является наиболее популярным методом кластеризации. Он был изобретён в 1950-х годах математиком Гуго Штейнгаузом и почти одновременно Стюартом Ллойдом.

1.2 Математическое описание алгоритма

Входные параметры: $n$ наблюдений (векторов) $(\mathbf x_1, \mathbf x_2, .. \mathbf x_n)$, $k$ - число кластеров.

Также входным параметром можно считать метрику для векторов, например евклидово расстояние $d(x, y) = \sum_{i = 1}^{l} (x_i - y_i )^2$ - одна из самых популярных используемых метрик.

Формально нам необходимо найти такое разделение $(\mathbf x_1, \mathbf x_2, .. \mathbf x_n)$ на подмножества $G = (G_1, .. G_k)$, минимизирующие сумму квадратов расстояний до их центров, или суммарное квадратичное отклонение:

$J = \underset{\mathbf{G}} {\operatorname{arg\,min}} \sum_{i=1}^{k} \sum_{\mathbf x \in G_i} d(\mathbf x, \boldsymbol\mu_i)^2,$

где $\boldsymbol\mu_i$ - центр кластера $G_i$

Алгоритм работает итерационно, каждая итерация алгоритма представляет собой следующее:

• Пересчитать центр масс для каждого кластера, полученного на предыдущем шаге: $\boldsymbol \mu_i = \frac{\sum_{\mathbf x_i \in G_i}\mathbf x_i}{|G_i|}, i = 1, 2, .. k$
• Переразбить векторы на кластеры в соответствии с расстоянием до новых посчитанных центров: $z_i = \underset{\mathbf{j}} {\operatorname{arg\,min}} \{d(\mathbf x_i, \boldsymbol \mu_j)\}, i = 1, 2, .. n$

Алгоритм завершается, когда на какой-то итерации не происходит изменения центра масс кластеров. Это происходит за конечное число итераций, так как количество возможных разбиений конечного множества конечно, а на каждом шаге суммарное квадратичное отклонение $J$ не увеличивается, поэтому зацикливание невозможно.

Такой алгоритм сходится при любом начальном приближении разбиения на кластеры, поэтому в качестве нулевого шага часто выбирают $k$ случайных векторов среди $(\mathbf x_1, \mathbf x_2, .. \mathbf x_n)$.

1.3 Вычислительное ядро алгоритма

Две основные составляющие алгоритма:

Вычислительное ядро алгоритма можно считать состоящим из двух частей:

• Пересчет расстояний ярлыков кластеров векторам. Это ядро подразумевает многократное вычисление евклидовых расстояний между $N$-мерными векторами.
• Пересчет новых центроидов. В этом ядре осуществляются в основном операции сложения $N$-мерных векторов.

1.4 Макроструктура алгоритма

Алгоритм представляет собой циклическое чередование двух этапов, описанных выше, причем каждый использует результаты предыдущего.

Так как расстояния векторов до центроидов никак не связаны друг с другом, подсчет этих расстояний выполняется параллельно друг другу.

1.5 Схема реализации последовательного алгоритма

Структура алгоритма описывается так:

1. Инициализация центроидов $\mu_1, ... \mu_k$.
2. Последовательное вычисление расстояний векторов до этих центроидов и разбиение по кластерам с этими центрами.
3. Нахождение изменения метрики $J$. Если оно меньше некоего заданного порога, то центроиды найдены.
4. Пересчет центроидов в новых кластерах.
5. Переход к шагу 2.

1.6 Последовательная сложность алгоритма

Пусть на входе $n$ векторов длины $N$, выделяется $k$ кластеров.

Вычислительная сложность подсчета квадрата расстояния между двумя векторами: $2N - 1$ сложений и вычитаний, $N$ умножений. Таким образом, сложность подсчета метрики $J$ для одной итерации: $n * k * (2N - 1)$ сложений, $n * k * N$ умножений. Пересчет кластеров (поиск среднего ариметического векторов в кластере): $(n - k) * N$ сложений, $k * N$ делений. Итого, если $I$ - число итераций, общая сложность: $(n * k *(2N - 1) + n * k * N + (n - k) * N + k * N) * I = (3N * n * k - n * k + n * N) * I$.

Таким образом, общая сложность: $O(NnkI)$

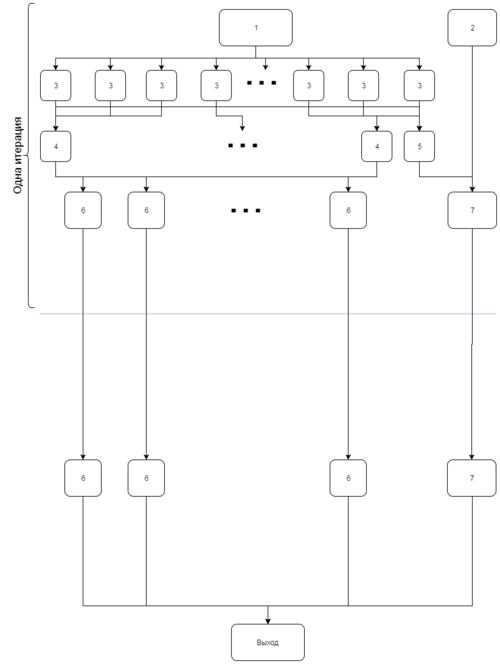
1.7 Информационный граф алгоритма

Рисунок 1. Информационный граф алгоритма k средних

1. Первичная инициализация центроидов
2. Первичная метрика
3. Подсчет расстояния между вектором и центроидом
4. Выбор кластера для вектора а основе расстояний до центроидов
5. Подсчет метрики J (сумма квадратов расстояний)
6. Расчет нового центроида
7. Сравнение новой метрики со старой

1.8 Ресурс параллелизма алгоритма

• Сложность второго яруса информационного графа составляет $3N - 1$ операций
• Сложность третьего яруса - $n * k - 1$ операций
• Сложность четвертого яруса - $(max(cluster size) - 1) * N + N = N * max(cluster size)$, где максимальный размер кластера зависит от входных данных, но на каждой итерации не больше $n - k + 1$

Итого сложность при максимальной параллелизации: $I * (3N - 1 + n * k - 1 + (n - k + 1) * N) = I * (4N - 2 + nk + nN - kN)$:

$O(n(k+N)I)$

1.9 Входные и выходные данные алгоритма

Входные параметры: $n$ векторов размерности $N$, $k$ - число кластеров

Объем входных данных: $O(N * n * k)$

Выходные данные: k центроидов

Объем выходных данных: $O(N * k)$

1.10 Свойства алгоритма

• Не гарантируется достижение глобального минимума суммарного квадратичного отклонения $J$, а только одного из локальных минимумов.
• Результат зависит от выбора исходных центров кластеров, их оптимальный выбор неизвестен.
• Число кластеров надо знать заранее.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

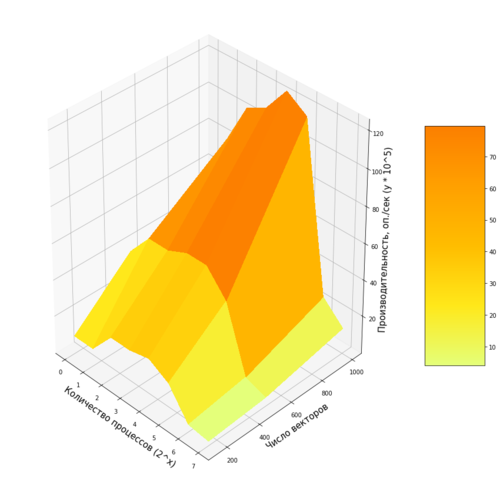
Изменяемые параметры запуска реализации алгоритма:

• Число процессоров: $[1, 2, 4, 8, 16, 32, 64, 128]$;
• Число векторов: $[150, 500, 100]$. Размерность $(N = 4)$ и число кластеров $(k = 4)$ не изменяется

На графике показана зависимость производительности (количество операций в секунду) от числа процессов и числа векторов.

Рисунок 2. Масштабируемость алгоритма k средних

2.7 Существующие реализации алгоритма

• C + MPI

3 Литература

• MacQueen, J. B. (1967). "Some Methods for classification and Analysis of Multivariate Observations"
• MacKay, David (2003). "An Example Inference Task: Clustering"
• Jing Zhang, Gongqing Wu, Xuegang Hu, Shiying Li, Shuilong Hao (2012). "A Parallel K-Means Clustering Algorithm with MPI"