Участник:Nbvehbectw/Алгоритм нахождения точек множества Мандельброта
Жалеев Тимур, группа 404.
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
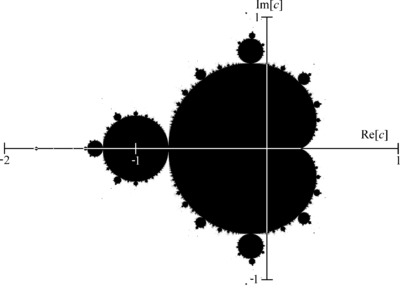
Множество Мандельброта - множество точек [math]c[/math] комплексной плоскости таких, что последовательность [math]z_{n+1} = z_n^2 + c, z_0 = 0[/math] ограничена[1]. Для изображения области множества выбирается некоторое количество итераций (обычно зависящее от размеров изображаемой области) и так называемый "радиус выхода", и для соответствующих [math]c[/math] из области вычисляются элементы данной последовательности. Если на всех итерациях модуль элемента остается не больше радиуса выхода, то считается, что последовательность ограничена, и данная точка принадлежит множеству. В противном случае последовательность считается уходящей в бесконечность, а точка - не принадлежащей множеству. Можно доказать, что если для какого-либо элемента последовательности выполняется [math]\left| z_n \right| \gt 2[/math], то последовательность не ограничена[1], то есть в качестве радиуса выхода можно взять число 2.
1.2 Математическое описание алгоритма
Для изображения прямоугольной области множества Мандельброта можно выбрать следующие параметры: координаты центра изображения [math](\overline{x}, \overline{y})[/math], ширина [math]W[/math] и высота [math]H[/math] изображения и расстояние между соседними пикселями [math]p[/math]. Тогда для каждого пикселя с координатами [math]i[/math] по горизонтали и [math]j[/math] по вертикали вычисляется число [math]c[/math] по следующим правилам:
[math]\operatorname{Re} \, c = \overline{x} + \left(i - \frac{W}{2}\right)p[/math]
[math]\operatorname{Im} \, c = \overline{y} - \left(j - \frac{H}{2}\right)p[/math]
Для полученных [math]c[/math] определяется их принадлежность множеству по указанному выше алгоритму с количеством итераций [math]O \left( \frac{1}{\sqrt p} \right)[/math][2] и радиусом выхода 2. В зависимости от того, определяется точка принадлежащей или не принадлежащей множеству, соответствующий ей пиксель окрашивается одним или другим цветом.
Также существуют различные способы построить изображение более наглядно с использованием цвета. Самый простой - окрашивать точки множества черным цветом, а остальные точки окрашивать различными цветами в зависимости от того, сколько потребовалось итераций [math]n[/math], чтобы элемент последовательности [math]z_{n+1} = z_n^2 + c, z_0 = 0[/math] превысил радиус выхода. Однако этот метод тоже дает изображение с резкими границами: число итераций - это всегда целое число, и образуются области, окрашенные одним цветом. Более гладкий способ окрашивания точек вне множества использует следующую формулу:
[math]\mu = n + 1 - \frac{\ln(\ln \left| z_n \right|)}{\ln 2}[/math],
где [math]n[/math] - число итераций, потребовавшееся для для превышения элементом последовательности радиуса выхода, а [math]z_n[/math] - этот элемент[3]. Для понимания сути этой формулы можно использовать описание, приведенное Earl L. Hinrichs:
«Игнорируя [math]+ c[/math] в обычной формуле, получим, что точки последовательности растут как [math]z := z^2[/math]. То есть у нас есть последовательность [math]z, z^2, z^4, z^8, z^{16}[/math], и т.д. Подсчет числа итераций означает присвоение целого числа этим значениям. Если игнорировать множитель, логарифм этой последовательности получится: [math]1, 2, 4, 8, 16[/math]». Логарифм логарифма: [math]0, 1, 2, 3, 4[/math], что соответствует целому значению из подсчета итераций. Таким образом, подходящим обобщением дискретного подсчета итераций на непрерывную функцию будет двойной логарифм»[3].
При использовании этой формулы число [math]\mu[/math] получается примерно равным [math]n[/math], однако меняющимся практически непрерывно по [math]c[/math].
Также заметим, что определение принадлежности точки ко множеству не зависит от других точек, то есть может выполняться параллельно. Также параллельно могут строиться сразу несколько изображений, например, с одним центром и убывающим расстоянием между пикселями для получения наглядной анимации "погружения" во множество Мандельброта.
