Участник:RS42/Quickhull

Тимофеев Александр Евгеньевич, группа 403

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Задача построения выпуклой оболочки является одной из важных проблем вычислительной геометрии. Выпуклую оболочку множества точек [math]X[/math] можно определить следующим образом: это пересечение всевозможных выпуклых множеств, содержащих [math]X[/math]. В случае конечного числа [math]n[/math] точек из [math]X[/math]:

[math]\mathrm{Conv}(X)=\left\{\left.\sum_{i=1}^{n} \alpha_i x_i\ \right| (\forall i: \alpha_i\ge 0)\wedge \sum_{i=1}^{n} \alpha_i=1 \right\}.[/math]

Алгоритм Quickhull позволяет провести построение в пространстве произвольной размерности [math]d[/math]. Результатом работы является множество [math]d-1[/math]-мерных граней (facets) и вершин (vertices) полученной выпуклой оболочки.

1.2 Математическое описание алгоритма

Наложим на множество [math]X[/math] следующее условие: любые [math]d+1[/math] точки аффинно независимы (что тождественно тому, что они не лежат в одной [math]d-1[/math]-мерной плоскости). Выпуклая оболочка будет задаваться списком вершин и граней. Следует отметить, что алгоритм представляет грани как [math]d-1[/math]-симплексы, а ребра как [math]d-2[/math]-симплексы. Таким образом, если в трехмерном случае привычная нам грань, образованная из четырех точек в одной плоскости, будет четырехугольником, то в представлении через симплексы она разбита на две грани в виде двух треугольников, разделенных одним общим ребром. Для каждой грани известны ее вершины, ее соседние грани и уравнение гиперплоскости, в которой эта грань лежит. Ребро (ridge) определяется как пересечение двух соседних граней и имеет размерность [math]d-2[/math]. Граница грани состоит из ребер.

Нам понадобится вычисление ориентированного расстояния от некоей точки [math]x[/math] до гиперплоскости (signed distance to hyperplane). Зададим начало координат в точке [math]O[/math], плоскость определяется единичной нормалью [math]\vec n[/math] и смещением [math]h[/math] относительно начала координат. Тогда ориентированное расстояние будет равно [math](\vec x, \vec n) + h[/math], где [math]\vec x = x - O[/math]. Точки на гиперплоскости удовлетворяют, собственно говоря, ее уравнению [math](\vec x, \vec n) + h = 0 [/math]. Если ориентированное расстояние положительно, то можно сказать, что точка находится выше плоскости (или плоскость видна из точки). В нашем случае все грани выпуклой оболочки во время построения будут иметь такие нормали и смещения, что для точек внутри оболочки расстояния до каждой плоскости будут неположительными.

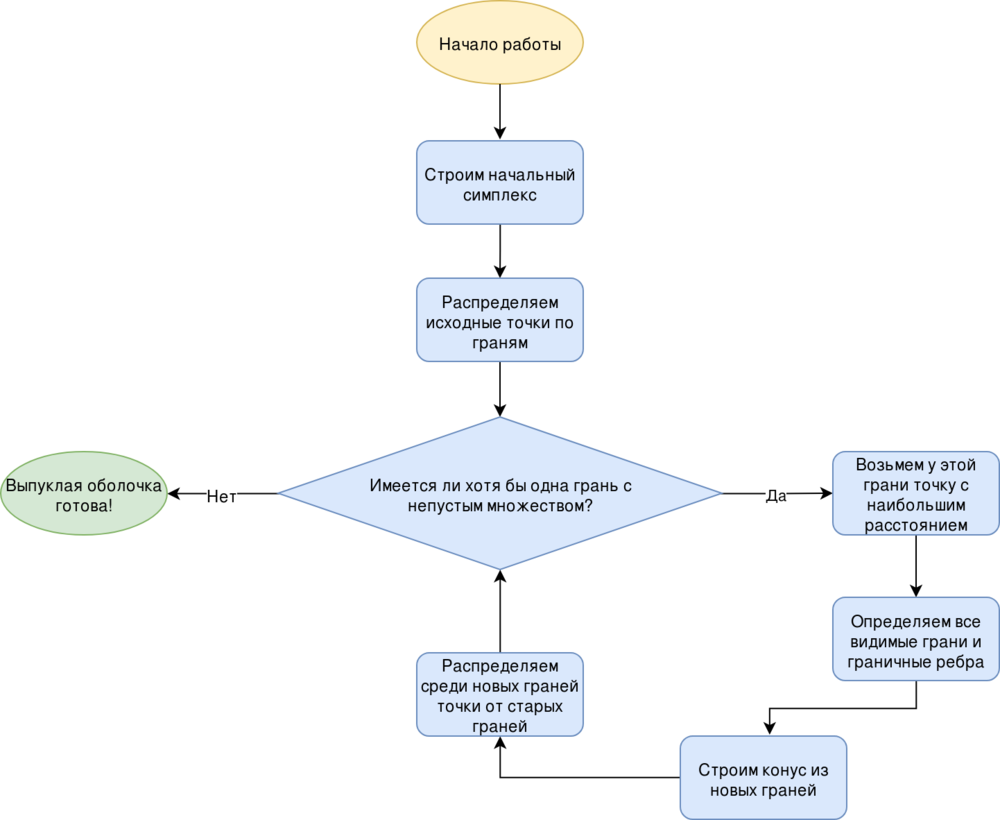
Рассмотрим сам алгоритм:

создать начальный d-симплекс
для каждой грани F
  для каждой нераспределенной точки p
    если p находится над F
      добавить p во множество внешних точек грани F
для каждой грани F с непустым множеством внешних точек
  выбрать наиболее отдаленную точку p из списка внешних точек грани F
  добавить F во множество видимых граней V
  для каждого непосещенного соседа N для граней из V
    если N видна из p
      добавить N в V
  граница множества V будет набором граничных ребер H
  для каждого ребра R из H
    построить новую грань из R и p
     соединить построенную грань с ее соседями
  для каждой новой грани G
    для каждой нераспределенной точки q из объединения множеств внешних точек граней из V
      если G видна из q
        добавить q во множество внешних точек G
  удалить грани из V

Стартовый симплекс, который по ходу работы алгоритма будет расти до окончательной оболочки, можно создать из любых [math]d+1[/math] точек, исходя из условия на [math]X[/math]. Но в реальности это условие общего положения (general position) можно заменить на требование возможности выбрать [math]d[/math]-мерный симплекс. Имеет смысл выбрать его таким образом, чтобы как можно больше точек уже оказалось в нем, поэтому его вершинами следует сделать точки с минимальными и максимальными координатами. Если таких точек не будет хватать, произведем добор произвольными.

Дальнейшие шаги алгоритма позволяют добавлять к промежуточной выпуклой оболочке новые вершины. По сути выбирается оптимальная в каком-то смысле внешняя точка [math]p[/math], а затем определяется множество [math]V[/math] видимых из этой точки граней. Данные видимые грани отделены от невидимых множеством граничных ребер (horizon ridges). Далее граничные ребра и точка [math]p[/math] образуют новые грани, видимые грани удаляются. Тем самым совершен переход к новой промежуточной выпуклой оболочке. Такое описание является обобщенным и ему также соответствует randomized incremental algorithm, в котором точка [math]p[/math] выбирается случайным образом. В нашем случае точка [math]p[/math] будет наиболее отдаленной точкой от плоскости текущей рассматриваемой грани [math]F[/math], что однако же не гарантирует присутствие [math]p[/math] в итоговой выпуклой оболочке. Также можно выбрать [math]p[/math] как наиболее отдаленную точку среди всех пар (грань-"самая дальняя точка этой грани"), но такой выбор на каждом шаге только увеличит время работы алгоритма.

Как решается проблема определения граничных ребер, когда уже выбрана точка [math]p[/math]? Множество внешних точек (outside set) грани [math]F[/math] представляет из себя множество точек (возможно не всех), из которых эта грань видна. Поэтому если [math]p[/math] из множества внешних точек грани [math]F[/math], то это означает, что [math]F[/math] будет видна из [math]p[/math], и следует начать поиск границы именно с соседей [math]F[/math]. Пусть [math]H[/math] - соседняя к [math]F[/math] грань. Если [math]H[/math] видна, то следует проверить таким же образом и соседей [math]H[/math]. Если [math]H[/math] не видна, то мы наткнулись на участок границы, и рассматривать соседей [math]H[/math] нет смысла.

Получив граничные ребра, строим новые грани. Требуется обновить списки соседей и понять, какие внешние точки были захвачены. Захватить мы могли только те точки, которые были внешними для уничтоженных на этом шаге граней. То есть множество таких точек - это объединение множеств внешних точек граней из [math]V[/math]. Распределяем эти точки по множествам внешних точек для новых граней.

Алгоритм будет продолжать свою работу до тех пор, пока не останется ни одного пустого множества внешних точек.

1.3 Вычислительное ядро алгоритма

В алгоритме можно выделить две трудоемкие части:

1. Распределение точек по множествам внешних точек.

Элементарная операция на данном этапе - вычисление расстояния от точки до плоскости, сложность [math]O(d)[/math].

2. Построение новых граней.

Основная операция - нахождение гиперплоскости по точкам, сложность [math]O(d^3)[/math]. На практике также присутствуют расходы по работе со структурами данных, представляющих выпуклую оболочку.

1.4 Макроструктура алгоритма

Рассмотрим подробнее процесс построения новой грани. Она получается путем взятия одного ребра ([math]d-1[/math] точка) из множества граничных ребер и прибавлением к этому ребру выбранной на данном этапе вершины. Тем самым возможно определение [math]d-1[/math] нового ребра, которые вместе с исходным составляют одну грань. Но полученные ребра также принадлежат и другим граням из строящегося конуса, которые попарно граничат с текущей гранью как раз по каждому из ребер. Для отслеживания уже построенных ребер можно использовать хэш-таблицу. Нахождение уравнения гиперплоскости по точкам [math]{x_i}, i=1,..,d[/math] может сводиться к решению системы [math]An=0[/math], где [math]A[/math] - матрица размера [math](d-1) \times d[/math], строки которой представляют из себя транспонированные векторы [math]x_i-x_1 , i=2,..,d[/math]. Например, это можно сделать с помощью [math]LUP[/math]. Затем несложно отыскать [math]f=-(n,x_1)[/math]. Далее следует убедиться, что ориентированное расстояние для точек внутри выпуклой оболочки будет отрицательно, для этого используется некая точка [math]c[/math], заведомо лежащая внутри. Ее можно выбрать в самом начале в качестве среднего значения точек начального симплекса.

1.5 Схема реализации последовательного алгоритма

1.6 Последовательная сложность алгоритма

Обозначим за [math]r[/math] число вершин итоговой выпуклой оболочки, а [math]f_r[/math] примем за максимальное число граней для [math]r[/math] вершин. Известно, что [math]f_r = O(r^{\lfloor d/2 \rfloor}/ \lfloor d/2 \rfloor!)[/math].

Авторы алгоритма приводят верхнюю оценку сложности для так называемого сбалансированного случая, и она составляет [math]O(n \ log \ r) [/math] при [math]d \leq 3[/math] и [math]O(n f_r / r)[/math] при [math]d \geq 4 [/math].

1.7 Информационный граф

Для начала рассмотрим простой параллельный вариант, требующий наименьшее количество пересылок.

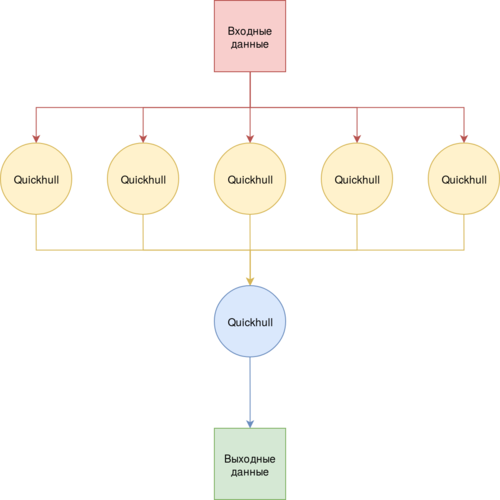
Мы можем распределить исходные точки по нескольким процессам, на каждом получить по одной выпуклой оболочке и переслать вершины итоговых построений одному процессу, который запустит процесс построения выпуклой оболочки, распределив полученные точки по множествам внешних точек уже построенной им выпуклой оболочки. Такой процесс слияния оболочек можно производить и попарно между процессами. Но теперь стоит вопрос эффективности шага распределения точек по граням. В случае простого перебора сложность слишком высока и выигрыша по сравнению с последовательной реализацией нет. Было бы иначе, если существовал недорогой способ пройти по выпуклой оболочке и собрать ее вершины таким образом, чтобы близкие друг к другу вершины были также близки и в передаваемом массиве. Тогда процесс распределения можно организовать более эффективно. Возьмем некую точку [math]p[/math] и попытаемся определить, лежит ли она внутри выпуклой оболочки или же снаружи, и если снаружи, то найдем одну грань, которая видна из [math]p[/math]. Возьмем некую грань [math]F[/math] и посчитаем расстояние от [math]F[/math] и соседних к [math]F[/math] граней до [math]p[/math]. Выберем наибольшее из найденных расстояний. Если оно положительно, то точка [math]p[/math] снаружи. Если оно отрицательно и является расстоянием от [math]F[/math] до [math]p[/math], то в силу того, что мы рассматриваем выпуклую оболочку, грань [math]F[/math] будет ближайшей к [math]p[/math] и мы можем с уверенностью сказать, что [math]p[/math] внутри. Если же наибольшее расстояние соответствует некоей иной грани из окрестности [math]F[/math], то продолжим поиск таким же способом. В силу того, что последовательные точки в массиве нераспределенных точек близки друг к другу, будет затрачено меньше времени на распределение, нежели полным перебором.

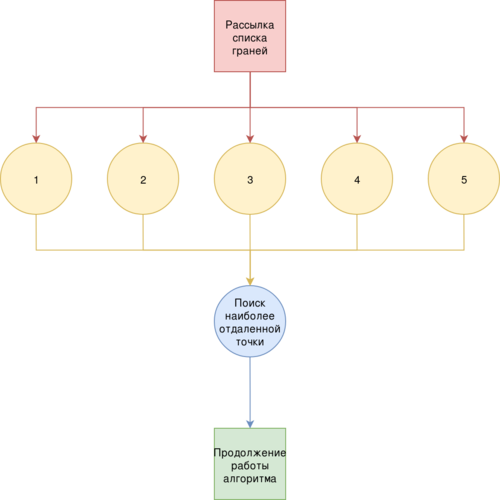
Ранее было уже указано на то, что существенную часть работы алгоритма составляет процесс распределения точек по множествам внешних точек. Этот процесс возможно распараллелить, когда как процесс построения новых граней имеет по большей части последовательную природу, и распараллелить там возможно разве что лишь решение системы. Итак, рассмотрим граф для процедуры распределения точек по множествам внешних точек. Эта процедура вызывается в двух местах алгоритма: один раз как распределение всех исходных точек по граням симплекса и при распределении точек из множеств старых граней по множествам для только что построенных.

Узлы с 1 по 5 содержат множества точек, которые требуется распределить по одному и тому же для каждого из узлов списку граней. Затем для каждой из граней этого списка определяется наиболее отдаленная точка, и алгоритм продолжает свою работу. Конечно, можно рассмотреть и противоположную схему: рассылка точек по узлам с гранями, но реализация на практике такой схемы намного сложнее.

1.8 Ресурс параллелизма алгоритма

Параллельная сложность алгоритма в случае рассмотренной выше схемы будет равна сложности построения новых граней, которая может быть оценена как [math]O(f_r)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные представляют из себя массив исходных точек. Требуется, чтобы из них можно было выбрать как минимум [math]d+1[/math] точку для начального [math]d[/math]-симплекса. На выходе получаем список граней, список ребер и вершины полученной выпуклой оболочки. Для граней известны их соседи через ребра и уравнения гиперплоскости.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Характеристики вычислительной среды: суперкомпьютер Ломоносов, версия MPI: intel mpi 5.0.1, компилятор: intel icc 15.0.0, ключи: -std=c++11, -O3.

Тестирование проводилось на множестве исходных точек, равномерно распределенных в единичном [math]d[/math]-мерном шаре. Для генерации входных данных использовался пакет Geometric Object Generators из библиотеки CGAL 4.8.2. Все тесты проводились для чисел процессов [math]2^k, k = 0,..,9[/math] и количества точек во входных данных [math]2^k, k = 12,..,24, d = 2, 3 [/math] и [math]2^k, k = 12,..,22, d = 4 [/math].

Для минимизации обменов производились избыточные вычисления: на каждом из узлов по ходу работы алгоритма строилась одна и та же оболочка. Операции обмена совершались только для передачи всем процессам вершины для построения новых граней и в самом начале работы алгоритма, когда один процесс производит рассылку выбранного им стартового симплекса.

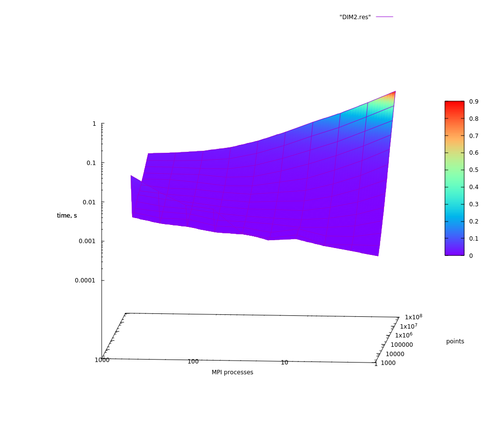
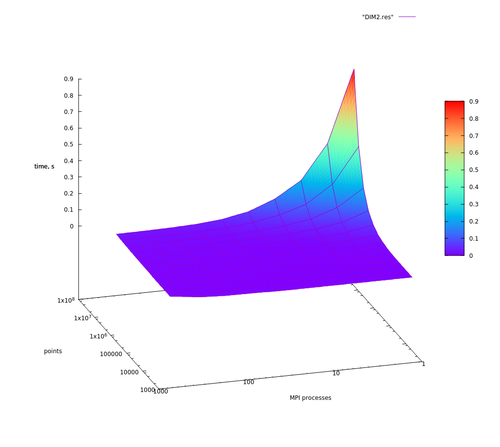
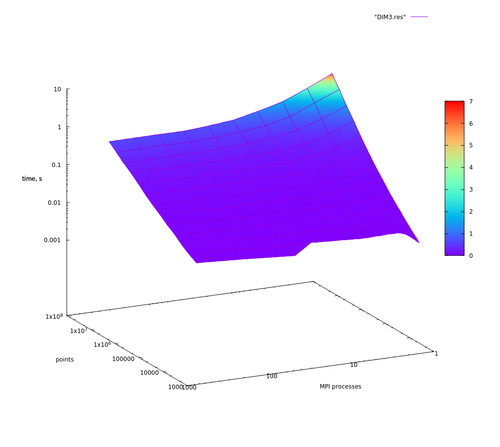
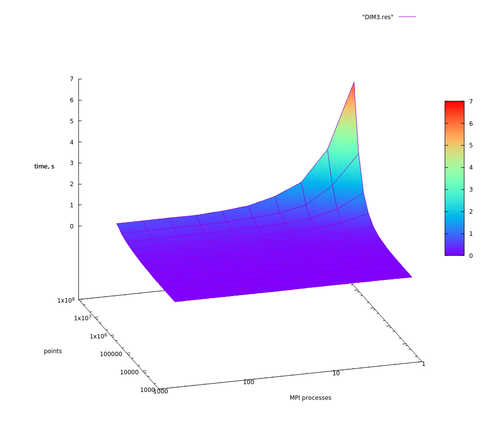
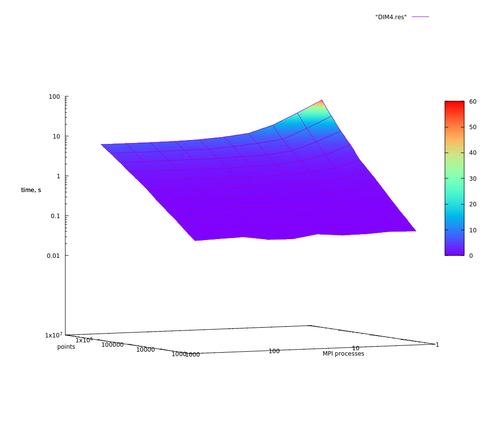
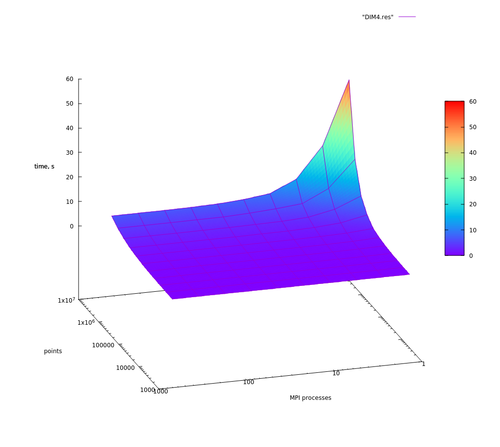
Далее для наглядности представлены графики времени выполнения алгоритма как в логарифмическом масштабе времени, так и в линейном. Хотя графики с линейным масштабом по времени только для того, чтобы быстро взглянуть и не задумываясь убедиться в том, что действительно есть какое-то ускорение.

Из описаний в пунктах 1.3 и 1.8 можно сделать предположения о работе алгоритма:

1. С ростом числа исходных точек растет время как операции распределения точек, так и операции построения новых граней. В силу того, что тестирование проводилось на точках, распределенных в шаре, доля времени операции распределения точек от общего времени будет только увеличиваться, и в итоге сложность всего алгоритма растет линейно на данных тестах. Это заметно на графиках, если зафиксировать число процессов. Если проводить тестирование на точках, лежащих на сфере, то с увеличением числа точек доля времени, ушедшего на построение новых граней, будет практически полностью составлять время работы всей программы.

2. Чем больше размерность задачи, тем большая доля времени уходит на построение новых граней.

3. При избыточном числе процессов следует ожидать даже замедление работы программы из-за возросших накладных расходов на пересылки.

На Рис. 1 и Рис. 3 можно отметить аномалии при 4096 точках во входных данных, что объясняется превышением времени на рассылки данных с помощью MPI_Bcast() по отношению как к операции построения новых граней, так и операции распределения точек.

Из сделанных предположений следует, что сильную масштабируемость для данной реализации мы можем наблюдать в том случае, если доля вычислений распределения точек составляет основную часть вычислений. На графиках видно, как при [math]2^{24}, 2^{23}, 2^{22}[/math] входных точках время работы обратно пропорционально числу процессов до определенного момента (64 узла для размерности 2 для [math]2^{24}[/math] точек, 4 узла для размерности 3 для [math]2^{24}[/math] и для размерности 4 с [math]2^{22}[/math] точек), когда время работы упирается во время последовательной части программы (см. закон Амдала), и дальнейшим ростом числа вычислительных узлов никак не помочь. И чем меньше входных точек, тем слабее проявляется сильная масштабируемость. С увеличением размерности задачи ситуация только ухудшается в силу возрастающей сложности операции построения новых граней.

• 

  Рис. 1. [math]d=2[/math]

• 

  Рис. 2. [math]d=2[/math]

• 

  Рис. 3. [math]d=3[/math]

• 

  Рис. 4. [math]d=3[/math]

• 

  Рис. 5. [math]d=4[/math]

• 

  Рис. 6. [math]d=4[/math]

2.7 Существующие реализации алгоритма

На момент написания данной статьи о существовании реализации алгоритма с помощью средств параллельных вычислений ничего неизвестно. В данной статье предложена реализация с использованием CUDA.

Последовательные реализации:

• Qhull - каноничная реализация от авторов алгоритма, обладающая широкими возможностями. Есть готовые пакеты во многих дистрибутивах.
• https://github.com/tomilov/quickhull - более компактная реализация на C++, описание доступно в виде статьи.

3 Литература

• Barber, C.B., Dobkin, D.P., and Huhdanpaa, H.T., "The Quickhull algorithm for convex hulls," ACM Trans. on Mathematical Software, 22(4):469-483, Dec 1996, http://www.qhull.org
• Clarkson , K. L., Mehlhorn , K., and Seidel , R. 1993. Four results on randomized incremental constructions. Comput. Geom. Theory Appl. 3, 185–211. Also in Lecture Notes in Computer Science. Vol. 577, pp. 463– 474.