Участник:Ruslanlazovskiy/CHAMELEON

Эта работа успешно выполнена Преподавателю: в основное пространство, в подстраницу Данное задание было проверено и зачтено. Проверено Kronberg и Algoman.

CHAMELEON
Последовательный алгоритм
Последовательная сложность	[math]O(n*m + n*log{n} + m*log{m})[/math]
Объём входных данных	[math]n^2 / 2[/math]
Объём выходных данных	[math]n[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(n)[/math] - этап 1. [math]O(q)[/math] - отдельная итерация этапа 3.
Ширина ярусно-параллельной формы	[math]O(n)[/math] - этап 1. [math]O(q)[/math] - отдельная итерация этапа 3.

Авторы статьи: Лазовский Р. А. (разделы 1.1 - 1.4 , 1.7 , 1.8), Мустафаев Э. Э. (разделы 1.5 , 1.6 , 1.9 , 1.10 , 2.2)

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

CHAMELEON – алгоритм динамической иерархической кластеризации графа, то есть процесса разбиения графа на несколько подграфов-кластеров таким образом, что данные внутри одного кластера имеют максимально схожи, а данные в разных кластерах — максимально различны. В классических алгоритмах кластеризации схожесть объектов определяется с помощью некоторой метрики (простейший пример — евклидова метрика). Не следует путать задачу кластеризации с задачей классификации: в последней характеристики объекта, необходимые для попадания в тот или иной класс, известны заранее, в рассматриваемой же задаче они становятся известны в процессе решения. Первоначально алгоритм был описан в статье.

Алгоритм CHAMELEON работает в 3 этапа. На первом этапе исходное множество объектов организуется в граф по принципу k ближайших соседей. На втором этапе этого граф разбивается на достаточно малые подграфы-кластеры. На третьем этапе происходит агломеративная иерархическая кластеризация полученных подграфов в соответствии с одной из выбранных метрик (возможные метрики будут подробно описаны далее). Число получаемых в итоге кластеров в явном виде не задаётся.

1.2 Математическое описание алгоритма

Исходные данные: Первоначально исходными данными алгоритма являются [math]n[/math] векторов длины [math]p[/math], каждый из которых соответствует одному объекту. На основании значений элементов этих векторов строится матрица смежности размера [math]n * n[/math], возможно сокращение требуемого объема памяти до [math](n*(n - 1))/ 2[/math] в соответствии с выбранной метрикой. К исходным данным также относится набор параметров. Это [math]k[/math] - количество ближайших соседей на первом этапе алгоритма, [math]q[/math] - отношение количества вершин в наибольшем подграфе по отношению к общему числу объектов на втором этапе алгоритма, а также параметры [math]T_{RI}, T_{RI}[/math] - пороговые значения, после которых прекращается агломеративная кластеризация на третьем этапе. Следует особо отметить, что число получаемых в итоге кластеров заранее не известно, хотя на него и можно повлиять изменением значений перечисленных параметров.

Первый этап алгоритма: На первом этапе на основании матрицы смежности строится граф [math]G = (V, E)[/math] [math]k[/math] ближайших соседей, где [math]V[/math] - множество вершин графа (т.е. объекты), а [math]E[/math] - множество ребер графа (т.е. построенные связи между ближайшими соседями). Указанный граф не обязательно является связным.

Второй этап алгоритма: Граф [math]G = (V, E)[/math] итеративно разбивается на множество подграфов [math]G_{i} = (V_{i}, E_{i}), i = 1 .. m[/math], где [math] \cup V_{i} = V, i = 1 .. m[/math]. Параметр [math]m[/math] явно не задаётся, выполнение этого этапа алгоритма прекращается по выполнении описанных далее условий. На каждой итерации выбирается [math]G_{b}[/math] с числом вершин, наибольшим среди всех подграфов, имеющихся на данной итерации. Этот граф разбивается на 2 подграфа [math]G_{bi}[/math] и [math]G_{bj}[/math] таких, что 1) [math]min(V_{bi},V_{bj}) \gt = 0.25 * V_{b}[/math] (имеется ввиду количество вершин) и 2) [math]\sum{E_{kl}}, E_{kl} = (v_{k}, v_{l}), v_{k} \in V_{bi} , v_{l} \in V_{bj} [/math] минимальна среди всех разбиений, удовлетворяющих 1). Итеративный процесс прекращается, когда [math]\sum{v_{b}} \lt = q * \sum{v} , v_{b} \in V_{b} , e \in E[/math] (имеется ввиду количество вершин). Здесь [math]q[/math] - задаваемый параметр, на практике он варьируется от [math]0.01[/math] до [math]0.05[/math]. Полученные подграфы называются малыми кластерами.

Третий этап алгоритма: Множество кластеров [math]G_{i} = (V_{i}, E_{i}), i = 1 .. m[/math] итеративно преобразуется в множество кластеров [math]G_{j} = (V_{j}, E_{j}), j = 1 .. l[/math], [math]l \lt = m[/math]. Для этого вводятся следующие понятия:

[math]EC_{(C_{i},C_{j})}[/math] - абсолютная взаимная связность пары кластеров [math]C_{i}, C{j}[/math]. Это суть сумма весов ребер, соединяющих вершины, принадлежащие [math]C{i}[/math] c вершинами из [math]C{j}[/math]. [math]EC_{(C_{i},C_{i})}[/math] вычисляется как сумма ребер, входящих в разделитель, разбивающий [math]C{i}[/math] на два равных подграфа.
[math]S_{EC_{(C_{i},C_{j})}}[/math] - абсолютное взаимное сходство пары кластеров [math]C_{i}, C{j}[/math]. Это суть среднее сходство между соединенными вершинами, принадлежащими [math]C{i}[/math] и [math]C{j}[/math] соответственно. Соединения обусловлены разбиением общего графа, полученного на первом этапе алгоритма.
[math]RI_{(C_{i},C_{j})} = \frac{2*|EC_{(C_{i},C_{j})}|}{|EC_{C_{i}}|+|EC_{C_{j}}|}[/math] - относительная взаимная связность пары кластеров [math]C_{i}, C{j}[/math]
[math] RC_{(C_{i},C_{j})}= \frac{S_{EC_{(C_{i},C_{j})}}}{\frac{|C_{i}|}{|C_{i}+C_{j}|}*S_{EC_{(C_{i})}}+\frac{|C_{i}|}{|C_{i}+C_{j}|}*S_{EC_{(C_{j})}}}[/math] - относительное взаимное сходство пары кластеров [math]C_{i}, C{j}[/math]

На основании этих показателей осуществляется агломеративная иерерхическая кластеризация. Существует две стратегии анализа показателей сходства. В первом случае для каждой пары кластеров [math]C{i}, C{j}[/math] проверяется истинность выражений [math]RI_{(C_{i},C_{j})} \gt = T_{RI}[/math] и [math]RC_{(C_{i},C_{j})} \gt = T_{RC}[/math], где [math]T_{RI}, T_{RI}[/math] - заранее заданные пороговые значения. Если для некоторого [math]C_{i}[/math] таких [math]C_{j}[/math] несколько, то конкретная пара определяется по максимуму значения [math]EC_{(C_{i},C_{j})}[/math]. Во втором случае выбираются пары кластеров, максимизирующие функцию вида [math]RI_{(C_{i},C_{j})}*RC_{(C_{i},C_{j})}^\alpha[/math]. Здесь [math]\alpha[/math] - заданный пользователем параметр. В обоих случаях процесс останавливается либо когда на очередной итерации не находится подходящих пар кластеров, либо когда остаётся только один кластер.

Вычисляемые данные: В процессе агломеративной кластеризации для всех объектов, т.е. всех вершин всех кластеров указывается индекс [math]j[/math] кластера, к которому они принадлежат. После завершения алгоритма возможно перенумеровать кластеры. В любом случае на выходе будет иметься [math]n[/math] значений, так как число объектов в процессе работы алгоритма не изменялось.

1.3 Вычислительное ядро алгоритма

В алгоритме 3 основных вычислительных ядра, по одному на каждый этап алгоритма.

На первом этапе алгоритма основная вычислительная нагрузка приходится на анализ матрицы смежности, необходимого для построения первоначального графа [math]G = (V, E)[/math], так как для каждого объекта необходимо перебрать всех его соседей и выделить [math]k[/math] ближайших по заданной метрике.

На втором этапе наибольшее время занимает поиск подходящего разбиения очередного подграфа. В элементарном варианте этой процедуры необходимо перебрать все комбинации вершин в этом подграфе, удовлетворяющие условию 1) из математического описания алгоритма, и для каждой из них подсчитать значение, используемое в 2).

На третьем этапе алгоритма вычислительное ядро полностью совпадает с самим этапом, то есть итерационным процессов агломеративной иерархической кластеризации, включающем в себя подсчёт выбранной метрики для каждой пары кластеров, имеющихся на очередной итерации.

1.4 Макроструктура алгоритма

Как уже понятно из предыдущих разделов описания, алгоритм CHAMELEON выполняется в 3 этапа, последовательных относительно друг друга. Каждый этап, строго говоря, соответствует отдельному алгоритму. В рамках этого описания макрооперациями будут считаться процедуры разбиения наибольшего подграфа на каждой итерации второго этапа алгоритма, а также процедура вычисления метрики для принятия решения об объединении кластеров на каждой итерации третьего этапа.

1.5 Схема реализации последовательного алгоритма

Схема представлена в виде C++-подобного псевдокода, макрооперации в алгоритме выделены в соответствии с предыдущим разделом описания.

 // First stage.
 int k // Number of neighbors.
 float v[n][p] // Initial vectors.
 float M[n][n] // Adjacency matrix.
 for (int i = 0; i < n; ++i) {
  for (int l = 0; l < n; ++l) {
   M[i][l] = Compute_metric(v[i],v[l]);
  }
 }
 Graph max_graph // Structure/class that represents a graph.
 Neighbor_list list // Here neighbors are initially stored.
 max_graph.add_vertices // Vertices ~ initial vectors.
 for (int i = 0; i < n; ++i) {
  for (int l = i + 1; i < n; ++i) { // "Smart" version - we do not repeat same vertex combinations.
   if (neighbor_number < k) {
     add_neighbor(v[i],v[l]) // Just add.
   }else{
     substitute_neighbor(v[i],v[l]) // Check whether a new element is closer than some of the oldies.
   }
  }
  max_graph.add_neighbors // Looks at neighbor lists of current vector and adds them
 }

 // Second stage. 
 float percent // Determines when to stop splitting graphs. 
 Graph graphs[n] // GRAPHS WILL MOST LIKELY TAKE LESS SPACE, IT'S JUST THE UPPER LIMIT. 
 max_graph = find_max_graph() // Biggest graph by number of vertices available. 
 while (graph_size(max_graph) > n * percent) {
   Split_graph(max_graph); // Split the graph - a macro operation that represents the second phase.
 }

 // Third stage. 
 Graph graphs[m] // That's how many graphs we got. m <= n. 
 bool pairs_exist // Check if the're pairs of clusters to unite.
 while (num_graphs > 1 && pairs_exist){
  pairs_exist = false // So we don't repeat if it fails.
  for (int i = 0; i < m; ++i) {
   for (int l = i + 1; l < m; ++l) { // Also a "Smart" version.
     check_pair(pairs_exist, graphs[i], graphs[l]); // Check whether graphs are similar enough by some metrics.
     if (pairs_exist) { Unite_graphs(graphs[i], graphs[l]) }; // Pairs_exist is set to true if something's found.
   }
  }
 }

1.6 Последовательная сложность алгоритма

Общая временная сложность последовательного варианта алгоритма CHAMELEON определяется как [math]O(nm + nlog{n} + mlog{m})[/math], где [math]n[/math] - число исходных объектов, [math]m[/math] - число малых кластеров, полученных после первого этапа работы. В случае "предельного" разбиения [math]m = n[/math] эта оценка превращается в [math]O(n^2)[/math]. В любом случае эта оценка не учитывает необходимости построения матрицы смежности по исходному набору векторов (авторы оригинальной статьи в своих исследованиях подразумевают, что матрица смежности уже построена), что означает дополнительные [math]O(n^2)[/math] операций. Тогда оценка будет составлять [math]O(n^2 + nm + nlog{n} + mlog{m})[/math] операций или [math]O(n^2)[/math] в случае "предельного" разбиения. Следует также обратить внимание, что это оценка по числу не сложений и умножений, а достаточно крупных операций. Например, вычисление метрики между двумя векторами рассматривается как одна операция, а она включает в себя [math]n[/math] умножений и [math]2n[/math] сложений (для вычисления квадратичной нормы разности векторов).

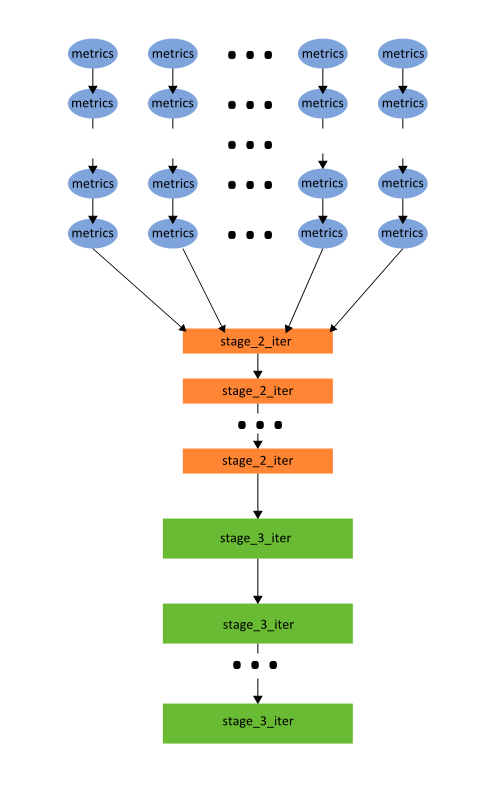
1.7 Информационный граф

Информационный граф дан в соответствии с макроструктурой алгоритма. Следует отметить, что имеются успешные попытки распараллелить 2 и 3 этапы алгоритма CHAMELEON (см. раздел "Существующие реализации"). Однако они включают в себя модификацию исходного алгоритма. Также возможно распараллеливание выборки пар кластеров и подсчёта их метрик внутри каждой из вершин stage_3_iter. Структура информационного графа внутри этих итераций аналогична структуре информационного графа первого этапа алгоритма.

1.8 Ресурс параллелизма алгоритма

Параллельную сложность алгоритма CHAMELEON следует оценивать отдельно для каждого этапа. На первом этапе алгоритм поиска [math]k[/math] ближайших соседей может быть выполнен за [math]n - 1[/math] вычислений значения метрики между двумя векторами. На втором этапе итерации алгоритма выполняются строго последовательно, а распараллеливание алгоритма внутри итерации не относится к теме статьи. На третьем этапе итерации также выполняются последовательно, однако возможно распараллеливание обработки пар кластеров внутри итерации. Каждая итерация может быть выполнена за [math]q - 1[/math] вычислений значения метрики между двумя кластерами, где q - количество кластеров на этой итерации.

1.9 Входные и выходные данные алгоритма

Входные данные:

[math]O[/math] - набор из [math]n[/math] векторов длины [math]p[/math].
[math]k[/math] - число, определяющиее количество ближайших соседей, по которым строится первоначальный граф.

Выходные данные:

[math]B[/math] - вектор длины [math]n[/math], значение [math]i[/math]-го элемента указывает на принадлежность соответствующего вектора одному из кластеров.

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности: Различные этапы алгоритма строго последовательны относительно друг друга. На первом этапе отношение последовательной сложности алгоритма к параллельной есть [math]n/2[/math]. На втором и третьем этапах различные итерации последовательны относительно друг друга. Однако внутри итераций допускается некоторый параллелизм. Например, для итераций третьего этапа в наилучшем случае отношение сложности последовательной реализации к параллельной есть [math]q/2[/math], где [math]q[/math] - число кластеров на конкретной итерации.

Вычислительная мощность: графовые алгоритмы, вообще говоря, обладают низкой вычислительной мощностью. В случае CHAMELEON вычислительная мощность первого этапа равна [math]O(1)[/math]. Для второго и третьего этапов оценка вычислительной мощности по сложениям и умножениям затруднительна, однако в терминах макроопераций можно дать грубую оценку. Вычислительная мощность каждой итерации второго этапа - [math]1 / \sum C_n^k[/math], где [math]n[/math] - число вершин в выбранном подграфе, а [math]k[/math] варьируется от [math]0.25 * n[/math] до [math]0.5 * n[/math]. Вычислительная мощность каждой итерации третьего этапа в этих терминах - [math]O(1)[/math].

Детерминированность: Важной особенностью описываемого алгоритма является его недетерминированность. Условия завершения как 2-го, так и 3-го этапа позволяют обозначить CHAMELEON как итерационный алгоритм с выходом по точности. При этом детерминированность 2-го этапа алгоритма можно обеспечить указанием вырожденных условий кластеризации (такая кластеризация, очевидно, не будет иметь практического смысла), в то время как 2-ый этап является недетерминированным всегда.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Как можно увидеть из раздела "существующие реализации", параллельной реализации алгоритма CHAMELEON на система с распределенной памятью найдено не было. Однако в . приводится экспериментальный вариант параллельной реализации посредством OpenMP для систем с общей памятью, включающий в себя значительную модификацию исходного алгоритма, но не приводится рабочая реализация.

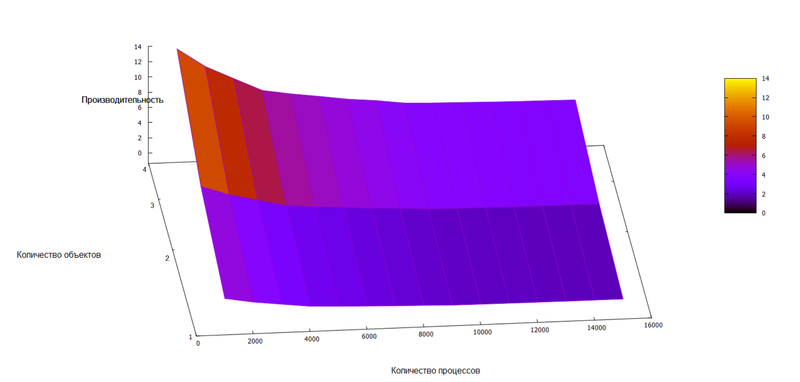
В силу вышескасновного основное внимание будет уделено исследованию масштабируемости алгоритма по размеру задачи, в пределах одного узла. Далее приводятся графики производительности в Гфлопс для различных размеров задачи. Эффективность работы алгоритма убывает на всей рассматриваемой области. Темпы убывания эффективности снижаются с ростом размера задачи.

Для исследования такой масштабируемости вширь использовалась референсная последовательная реализация алгоритма (cм. раздел "Существующие реализации"). Соответствующая программа запускалась на системе BG/P на одном вычислительном узле. Характеристики вычислительного узла, а также микропроцессорного ядра - элемента такого узла, приводятся в Таким образом, удостоверенными экспериментальными данными являются только значения, полученные для случая 1 процесса. Значения для случаев 2 и 4 процессов являются ОЦЕНОЧНЫМИ и выводятся из результатов работы модифицированной версии алгоритма, исследуемой в . К сожалению, указанной реализации авторы не предоставляют.

2.7 Существующие реализации алгоритма

С копией референсной реализации иерархической кластеризации, взятой с данного ресурса Sequental, в случае неработоспособности последнего, можно ознакомиться здесь Copy
Последовательная реализация алгоритма CHAMELEON использовалась в статье Теоретически возможна реализация алгоритма CHAMELEON с использованием графовых библиотек, например METIS , hMETIS и RANN.
Параллельных реализаций алгоритма CHAMELEON в графовых библиотеках мною найдено не было. Однако существует исследование, связанное с реализацией CHAMELEON посредством технологии OpenMP, с которым можно ознакомиться здесь параллельная реализация.

3 Литература

<references \>

Краткий обзор алгоритма [1]
Первоначальная статья от авторов алгоритма [2]

Исследования возможной параллелизации алгоритма[3]