Участник:Vagabond/Алгоритм быстрого дискретного пребразования Фурье
 | Эта работа успешно выполнена Преподавателю: в основное пространство, в подстраницу Данное задание было проверено и зачтено. Проверено Kronberg и IgorS. |
Автор: Данилишин А.Р.
Содержание
- 1 ЧАСТЬ. Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 ЧАСТЬ. Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 ЧАСТЬ. Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Пусть [math]X=(x_{1},...,x_{n-1})^{T}[/math] - исходный сигнал, который необходимо преобразовать умножением на тензор второго ранга [math]E_{pk}=e^{\frac{-2kpi\pi}{n}} [/math]. Результатом данного преобразования ([math]E*X[/math]) будет вектор [math]Y=(y_{1},...,y_{n-1})^{T}[/math], где [math] y_{p}=\sum_{k=0}^{n-1}x_{k}e^{\frac{-2kpi\pi}{n}}, p=\overline{0,n-1}[/math]. Данная формула является классической формулой ДПФ. Известно, что в общем случае умножение матрицы на вектор требует [math]O(n^{2})[/math] арифметических операций, поэтому возникает вопрос о сокращении данного количества.
Главная идея БПФ состоит в сокращении многочисленных повторов сложения и умножения, которые выполняются в ДПФ (повторяющиеся множители: [math]e^{\frac{-2kpi\pi}{n}}[/math] Например при условии, что [math](pk)mod(n)=const[/math], при всех [math]k=\overline{0,n-1}[/math] и [math]p=\overline{0,n-1}[/math]
За счет использования данного факта, происходит значительное сокращение количества вычислительных операций. В данной статье используется алгоритм Cooley – Tukey, который предполагает собой разбиение исходного множества входных сигналов на два равных подмножества. При этом множество входных сигналов должно быть степенью двойки. Далее операция деления множества продолжается для образовавшихся подмножеств, и так далее. В результате над каждым из полученных подмножеств выполняется БПФ. Данные вычисления можно выполнять независимо друг от друга. Этот факт используется для реализации параллельной версии алгоритма.
1.2 Математическое описание алгоритма
- Пусть [math]e^{\frac{-2kpi\pi}{n}}[/math] = [math]\omega _{n}^{kp}[/math].
- Разобьем исходный сигнал [math]x(n)[/math] на два подмножества, с четными [math]x_{1}(2n)[/math] и нечетными [math]x_{2}(2n+1)[/math] номерами.
Тогда получаем: [math]y_{p}=\sum_{k=0}^{n-1}x_{k}\omega _{n}^{kp}= \sum_{k=0}^{\frac{n}{2}-1}x_{2k}\omega _{n}^{2kp}+\sum_{k=0}^{\frac{n}{2}-1}x_{2k+1}\omega _{n}^{(2k+1)p}[/math].
Выпишем два свойства омеги:
- [math]\omega_{\frac{n}{2}}=e^{2(\frac{-2i\pi}{n})}=\omega_{n}^{2}[/math]
- [math]\omega_{n}^{\frac{n}{2}}=e^{\frac{-2ni\pi}{2n}}=e^{-i\pi}=-1[/math]
Воспользуемся первым: [math]y_{p}= \sum_{k=0}^{\frac{n}{2}-1}x_{2k}\omega _{n}^{2kp}+\omega_{n}^{p}\sum_{k=0}^{\frac{n}{2}-1}x_{2k+1}\omega _{n}^{2kp}=\sum_{k=0}^{\frac{n}{2}-1}x_{2k}\omega _{\frac{n}{2}}^{kp}+\omega_{n}^{p}\sum_{k=0}^{\frac{n}{2}-1}x_{2k+1}\omega _{\frac{n}{2}}^{kp}[/math]. Или, если обозначить [math]y_{1}(p)=\sum_{k=0}^{\frac{n}{2}-1}x_{2k}\omega _{\frac{n}{2}}^{kp}[/math], а [math]y_{2}(p)=\sum_{k=0}^{\frac{n}{2}-1}x_{2k+1}\omega _{\frac{n}{2}}^{kp}[/math], то получим формулу для вычисления координат изображения БПФ при [math]p=\overline{0...n/2}[/math]: [math]y_(p)=y_{1}(p)+\omega_{n}^{p}y_{2}(p)[/math].
Заметим, что [math]y(p); y_{1}(p); y_{2}(p)[/math] обладают свойством периодичности, с периодом [math]\frac{n}{2}[/math]. Покажем это для [math]y_{1}(p)[/math] : [math]y_{1}(p+\frac{n}{2})=\sum_{k=0}^{\frac{n}{2}-1}x_{2k}\omega_{\frac{n}{2}}^{k(p+\frac{n}{2})}=\sum_{k=0}^{\frac{n}{2}-1}x_{2k}\omega_{\frac{n}{2}}^{kp}\omega_{\frac{n}{2}}^{\frac{kn}{2}}=\sum_{k=0}^{\frac{n}{2}-1}x_{2k}\omega_{\frac{n}{2}}^{kp}[/math]
Так как: [math]\omega_{\frac{n}{2}}^{\frac{kn}{2}}=e^{\frac{-4kni\pi}{2n}}=e^{-2ki\pi}=1[/math]
Далее необходимо определить [math]y(p)[/math] при [math]p\geq \frac{n}{2}[/math]. Теперь воспользуемся свойством периодичности обнаруженными нами ранее: [math]y(p+\frac{n}{2})=y_{1}(p+\frac{n}{2})+\omega_{n}^{(p+\frac{n}{2})}y_{2}(p+\frac{n}{2})[/math]. Воспользуемся вторым свойством омеги: [math]y(p)=y_{1}(p)-\omega_{n}^{p}y_{2}(p)[/math]. Все выкладки, приведенные выше, относятся ко второму этапу алгоритма Cooley – Tukey, который был использован в данной статье. Последующие шаги данного этапа делят подмножества полученные на предыдущем шаге вычисления БПФ.
В конечном итоге вышеупомянутый алгоритм сводится к двум этапам:
Бит-реверсирование
Бит-реверсирование – это преобразование двоичного числа путем изменения порядка следования бит в нем на противоположный. Бит-реверсирование применимо только к индексам элементов массива и предназначено для изменения порядка следования этих элементов, при этом значения самих элементов не изменяются. Так, к примеру, четырехмерный вектор [math](x_{0},x_{1},x_{2},x_{3})[/math] изменится на [math](x_{0},x_{2},x_{1},x_{3})[/math]. Данная процедура необходима для разделения исходного сигнала на элементы подмножеств с четными и нечетными номерами, которые необходимы для вычисления [math]y_{1}(p)[/math] и [math]y_{2}(p)[/math].
Вычисление БПФ
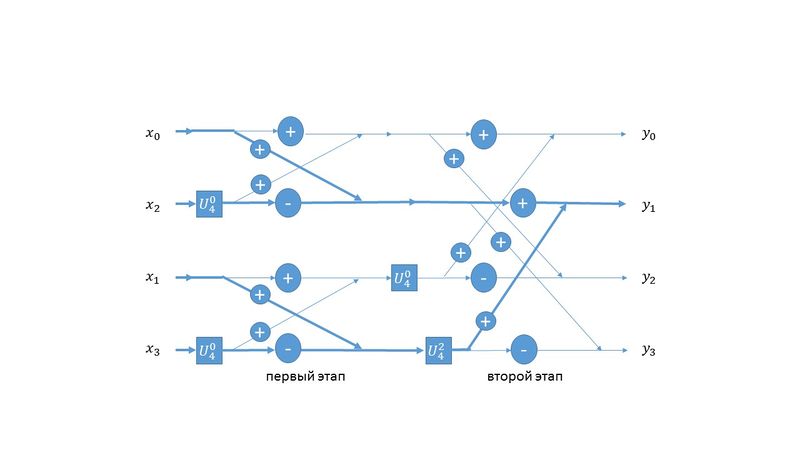
После выполнения этапа бит-реверсирования выполняются вычисления проиллюстрированные на рисунке 1 в разделе Информационный граф. Рисунок 1 приведен для случая четырехмерного входного сигнала. Он предполагает совершение двух этапов. В общем же количество этапов равно [math]log_{2}n[/math]. Каждый этап содержит в себе вычисление одной и той же операции "бабочки", где на вход подаются два числа [math]a[/math] и [math]b[/math], на выходе же получаются [math]a+bU[/math] и [math]a-bU[/math], где [math]U[/math]- это коэффициент поворота. Общая формула для коэффициента поворота: [math]e^{\frac{-ji\pi}{k}}[/math], где [math]k[/math]- размер шага "бабочки", [math]j[/math]- номер итерации вычислений над группой элементов, размером [math]2k[/math] [math](0\leq j \lt k )[/math].
1.3 Вычислительное ядро алгоритма
Из двух вышеописанных этапов БПФ, бит-реверсирование является самым быстровыполнимым. Поэтому вычислительное ядро алгоритма будет лежать именно во втором этапе. А именно, им будет являться вычисление "бабочек". Количество этапов выполнения БПФ, как описывалось выше, равно [math]log_{2}n[/math]. Учитывая количество этапов, размерность входного сигнала и идею деления на подмножества, всего "бабочек" получается [math]\frac{nlog_{2}n}{2}[/math]. При этом операция умножения выполняется [math]\frac{n}{2}[/math] раз. Это связано с тем, что результаты вычисления "бабочки" [math]a+bU[/math] и [math]a-bU[/math].
1.4 Макроструктура алгоритма
Из всего вышесказанного заключаем, что макроструктуру алгоритма легче всего описать при помощи рекурсии:
- [math]\frac{n}{2}[/math] преобразований Фурье порядка 2
- умножение [math]\frac{n}{2}[/math] пар комплексных чисел
- [math]n[/math] комплексных сложений
- снова преобразование Фурье
Также необходимо заметить, что количеством рекурсий будет количество этапов выполнения БПФ, то есть глубина рекурсии будет равняться [math]log_{2}n[/math]
1.5 Схема реализации последовательного алгоритма
Программный код (описан на языке С++) строится из ряда функций:
- бит-реверсирование
- инициализация размерности входного сигнала
- инициализация входного сигнала (при помощи генератора случайных чисел)
- процесс очистки памяти
- выполнение операции "бабочка"
- выполнение БПФ
- функция вывода результата (для тестирования)
главный программный код БПФ:
int main()
{
complex<double> *inputSignal = NULL;
complex<double> *outputSignal = NULL;
int size = 0;
cout << "FFT. Serial version." << endl;
ProcessInitialization(inputSignal, outputSignal, size);
bit(inputSignal, outputSignal, size);
SerialFFTCalculation(outputSignal, size);
PrintSignal(outputSignal, size); //в случае тестирования
ProcessTermination(inputSignal, outputSignal);
cin.get();
}1.5.1 функция бит-реверсирования
void bit(complex<double> inputSignal[], complex<double> *outputSignal, int size)
{ // процесс бит-реверсирования
int j = 0, i = 0;
while (i < size)
{
if (j > i)
{
outputSignal[i] = inputSignal[j];
outputSignal[j] = inputSignal[i];
}
else
if (j == i)
outputSignal[i] = inputSignal[i];
int m = size >> 1;
while ((m >= 1) && (j >= m))
{
j -= m;
m = m >> 1;
}
j += m;
i++;
}
}1.5.2 инициализация размерности входного сигнала
void ProcessInitialization(complex<double>* &inputSignal, complex<double>* &outputSignal, int &size)
{
// инициализация размера входного сигнала
do
{
cout << "Enter the input signal length: ";
cin >> size;
if (size < 4)
cout << "Input signal length should be >= 4" << endl;
else
{
int tmpSize = size;
while (tmpSize != 1)
{
if (tmpSize % 2 != 0)
{
cout << "Input signal length should be powers of two" << endl;
size = -1;
break;
}
tmpSize /= 2;
}
}
}
while (size < 4);
cout << "Input signal length = " << size << endl;
inputSignal = new complex<double>[size];
outputSignal = new complex<double>[size];
DummyDataInitialization(inputSignal, size);
}1.5.3 инициализация входного сигнала
void DummyDataInitialization(complex<double>* mas, int size)
{
for (int i = 0; i < size; i++)
{
mas[i] = int(rand() % 100);
}
}1.5.4 процесс очистки памяти
void ProcessTermination(complex<double>* &inputSignal, complex<double>* &outputSignal)
{
//очистка памяти
delete[] inputSignal;
inputSignal = NULL;
delete[] outputSignal;
outputSignal = NULL;
}1.5.5 выполнение операции "бабочка"
void Butterfly(complex<double> *signal, complex<double> &u,int offset, int butterflySize)
{
complex<double> tem = signal[offset + butterflySize] * u;
signal[offset + butterflySize] = signal[offset] - tem;
signal[offset] += tem;
}1.5.6 выполнение БПФ
void SerialFFTCalculation(complex<double> *signal, int size)
{
int m = 0;
for (int tmp_size = size; tmp_size > 1; tmp_size /= 2, m++);
for (int p = 0; p < m; p++)
{
int butterflyOffset = 1 << (p + 1);
int butterflySize = butterflyOffset >> 1;
double coeff = M_PI / butterflySize;
for (int i = 0; i < size / butterflyOffset; i++)
for (int j = 0; j < butterflySize; j++)
Butterfly(signal,complex<double>(cos(-j*coeff),sin(-j*coeff)),j+i*butterflyOffset,butterflySize);
}
}1.5.7 функция вывода результата (для тестирования)
void PrintSignal(complex<double> *signal, int size)
{
cout << "Result signal" << endl;
for (int i = 0; i < size; i++)
cout << signal[i] << endl;
}1.6 Последовательная сложность алгоритма
Рассмотренный алгоритм Cooley – Tukey выполняется за [math]nlog_{2}n[/math] операций комплексного сложения и [math]\frac{n}{2}log_{2}n[/math] операций комплексного умножения. Таким образом последовательная сложность алгоритма является линейно-логарифмической.
1.7 Информационный граф
1.8 Ресурс параллелизма алгоритма
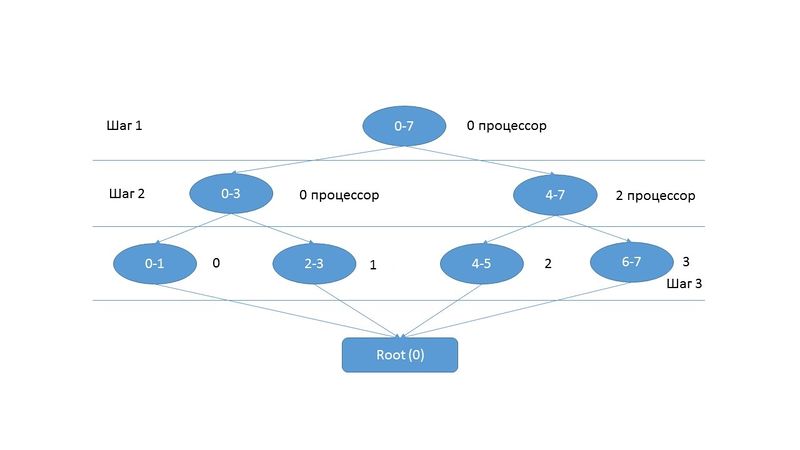
Рисунок 2 получен из информационного графа, главной идеей которого является процедура деления множеств полученных на предыдущем шаге на два равных по мощности подмножества и применение к ним БПФ. То есть процесс вычисления распределяется между [math]\frac{n}{2}[/math] процессорами. И так как при последовательной реализации алгоритма было [math]\frac{n}{2}\log_{2}n[/math] операций комплексного умножения и [math]n\log_{2}n[/math] комплексного сложения/вычитания. Получается, что при параллельной реализации алгоритма мы будем иметь [math]\log_{2}n[/math] операций комплексного умножения и [math]2\log_{2}n[/math] комплексного сложения/вычитания. При этом, если используется функция HT(Hyper threading), то параллельная сложность быстрого преобразования Фурье (базовый алгоритм Кули-Тьюки) для векторов с длиной, равной степени двойки составляет [math]\log_{2}n[/math].
1.9 Входные и выходные данные алгоритма
- Вещественное ДФП
- входные данные:
- вектор [math]\overline{a}=(a_{1},a_{2},...,a_{N})[/math], где [math]a_{i}\in \mathbb{R}[/math]
- размерность: [math]N[/math] точек
- выходные данные:
- вектор [math]\overline{b}=(b_{1},b_{2},...,b_{N})[/math], где [math]b_{i}\in \mathbb{C}[/math]
- размерность: [math]2N[/math] точек
- входные данные:
- Комплексное ДФП
- входные данные:
- вектор [math]\overline{a}=(a_{1},a_{2},...,a_{N})[/math], где [math]a_{i}\in \mathbb{C}[/math]
- размерность: [math]2N[/math] точек
- выходные данные:
- вектор [math]\overline{b}=(b_{1},b_{2},...,b_{N})[/math], где [math]b_{i}\in \mathbb{C}[/math]
- размерность: [math]2N[/math] точек
- входные данные:
1.10 Свойства алгоритма
- Соотношение последовательной и параллельной сложности является линейным. Это хорошо видно из пункта ресурс параллелизма алгоритма.
- Вычислительная мощность алгоритма является логарифмической.
- Устойчивость.
- Рассмотрим вопрос об устойчивости поближе. Так как БПФ отличается от ДПФ простым лишь сокращением одинаковых операций, то вопрос устойчивости можно рассматривать на примере ДПФ. Так, к примеру, возьмем формулу ДПФ и добавим возмущение: [math] y_{p}=\sum_{k=0}^{n-1}(x_{k}+\varepsilon )e^{\frac{-2*\pi*k*p*i}{n}}, p=\overline{0,n-1}[/math]. После чего преобразуем ее: [math]y_{p}=\sum_{k=0}^{n-1}x_{k}e^{\frac{-2*\pi*k*p*i}{n}}+\varepsilon\sum_{k=0}^{n-1} e^{\frac{-2*\pi*k*p*i}{n}}[/math] и оценим вторую сумму, которая является геометрической прогрессией со знаменателем [math]q=e^{\frac{-2*\pi*p*i}{n}}[/math]. Таким образом оцениваемая сумма будет равняться: [math]\varepsilon\frac{1-e^{\frac{-2*\pi*p*i*(n-1))}{n}}}{1-e^{\frac{-2*\pi*p*i}{n}}}[/math]. При достаточно больших размерностях входного сигнала данное выражение сводится к: [math]\varepsilon (1-e^{-2*\pi*p*i})[/math]. В тригонометрической форме данного выражения: [math]\varepsilon (cos(\frac{2*\pi*p*(n-1)}{n})-i*sin(\frac{2*\pi*p*(n-1)}{n}))[/math] видно, что принимая во внимание целочисленность индексов [math]p[/math] получается 0. Таким образом, мы можем говорить об устойчивости алгоритма в целом, и абсолютной устойчивости алгоритма в асимптотике.
- исходя из информационного графа, можно сделать вывод о сбалансированности алгоритма.
- алгоритм полностью детерминирован.
- Степень исхода вершины информационного графа не превышает двух.
2 ЧАСТЬ. Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Вычисления проводились на суперкомпьютере «Ломоносов».
Основные технические характеристики суперкомпьютера "Ломоносов":
- Пиковая производительность: 1,7 Пфлопс
- Производительность на тесте Linpack: 901.9 Тфлопс
- Число вычислительных узлов х86: 5 104
- Число графических вычислительных узлов: 1 065
- Число вычислительных узлов PowerXCell: 30
- Число процессоров/ядер x86: 12 346 / 52 168
- Число графических ядер: 954 240
- Оперативная память: 92 ТБ
- Общий объем дисковой памяти вычислителя: 1,75 ПБ
- Основной тип процессора: Intel Xeon X5570/Intel Xeon 5670, Nvidia X2070
- Число типов вычислительных узлов: 8
- Основной тип вычислительных узлов: TB2-XN
- Все узлы связаны тремя независимыми сетями:
- Системная сеть - QDR InfiniBand, 40 Гбит/сек
- Сервисная сеть - Ethernet, 10 Гбит/сек, 1 Гбит/сек и 100 Мбит/сек
- Управляющая сеть - Ethernet, 10 Гбит/сек и 1 Гбит/сек
- Сеть барьерной синхронизации и сеть глобальных прерываний, Т-Платформы
При работе была использована библиотека FFTW последней версии (3.3.5). Скрипт mpicxx с компилятором Intel. Вычислительные узлы х86. Код исследуемой программы представлен в разделе Существующие реализации алгоритма.
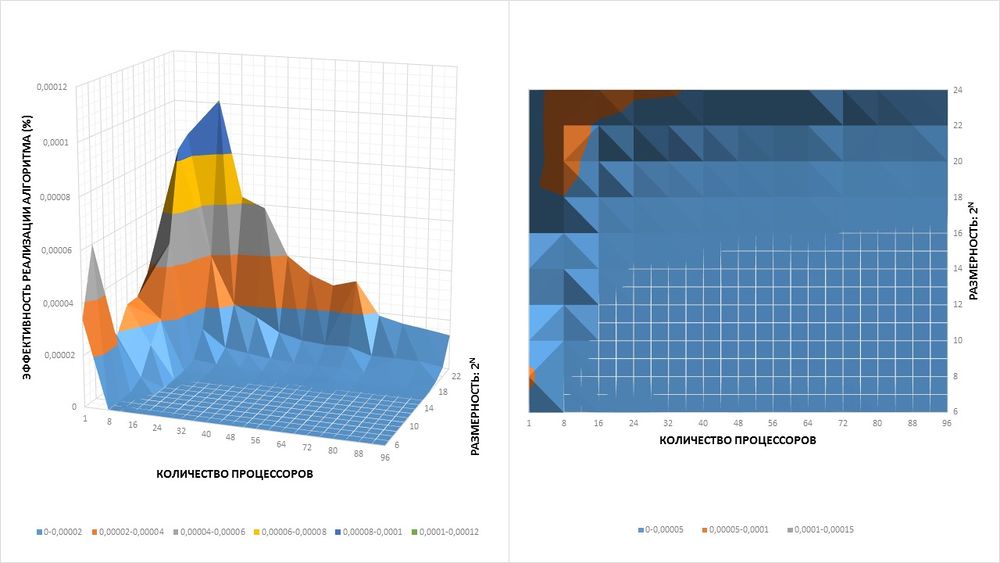
Как описывалось выше, каждый процессор получает достаточно низкий объем работы, что приводит к неэффективному распараллеливанию алгоритма (высокие затраты на передачу данных между процессорами по сравнению с вычислениями на них). Поэтому необходимо находить оптимальное количество процессоров для каждой отдельно взятой задачи. В данном примере, при размерности входного сигнала менее 262144, оптимальное количество процессоров составляет 1. При размерности 262144-4194304 оптимум достигался при 8 процессорах. И при размерности более 4194304- 16 процессоров.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Самой распространенной и известной реализацией дискретного БПФ является библиотека FFTW, разработанная Маттео Фриго и Стивеном Г. Джонсоном в Массачусетском технологическом институте. Данная библиотека существует для языков C и FORTRAN и позволяет производить вычисления в одном или нескольких измерениях. Входной сигнал может быть как действительным так и комплексным, а его размерность не обязательно должна быть степенью двойки. На данный момент последняя версия FFTW 3.3.5. Другие особенности библиотеки:
- Скорость. (Поддержка SSE / SSE2 / Altivec, начиная с версии 3.0. Версия 3.3.1 поддерживает AVX и ARM Neon.)
- Параллельные вычисления (OpenMP, MPI).
- Документация в форматах HTML, PDF.
- Данное программное обеспечение является свободным и распространяется по лицензии GNU (General Public License).
Здесь приводится пример реализации прямого БПФ для комплексных данных входного сигнала на языке C++.
#include <fftw3-mpi.h>
# include <stdlib.h>
# include <stdio.h>
#include <sys/stat.h>
#include <fcntl.h>
# include <time.h>
#include <math.h>
int main(int argc, char **argv)
{
const ptrdiff_t N0 = 4194304;
fftw_plan planForw;
fftw_complex *data, *dataOut;
ptrdiff_t alloc_local, local_ni, local_i_start, i, j, local_no, local_o_start;
int index, size;
double startwtime, endwtime;
MPI_Init(&argc, &argv);
fftw_mpi_init();
MPI_Comm_rank(MPI_COMM_WORLD, &index);
MPI_Comm_size(MPI_COMM_WORLD, &size);
/* get local data size and allocate */
alloc_local = fftw_mpi_local_size_1d(N0, MPI_COMM_WORLD, FFTW_FORWARD, FFTW_ESTIMATE,
&local_ni, &local_i_start, &local_no, &local_o_start);
data = fftw_alloc_complex(alloc_local);
dataOut = fftw_alloc_complex(alloc_local);
/* create plan */
planForw = fftw_mpi_plan_dft_1d(N0, data, dataOut, MPI_COMM_WORLD,
FFTW_FORWARD, FFTW_ESTIMATE);
/* initialize data to some function my_function(x,y) */
for (i = 0; i < local_ni; ++i)
{
data[i][0] = rand() / (double)RAND_MAX;
data[i][1] = rand() / (double)RAND_MAX;
}
if (index == 0){
startwtime = MPI_Wtime();
}
fftw_execute(planForw);
if (index == 0){
endwtime = MPI_Wtime();
printf("wall clock time = %f\n",
endwtime - startwtime);
}
fftw_destroy_plan(planForw);
MPI_Finalize();
}Скачав библиотеку и установив ее на рабочий компьютер, можно поэкспериментировать, используя вышеописанный исходный код. При этом, на стадии компиляции необходимо указывать директорию, где находятся заголовочные файлы и директорию, где находятся библиотечные файлы. Пример: mpicxx name.cpp -I/path/to/include/files -L/path/to/lib/files -lfftw3_mpi -lfftw3 -lm. Для версии 2.1.4 описание на русском языке приводится здесь.
Остальные реализации:
- GSL - GNU Scientific Library
- cuFFT
- Engineering and Scientific Subroutine Library (ESSL) and Parallel ESSL
3 Литература
[1] Бахвалов Н. С., Жидков Н. П., Кобельков. Г. М. — 6-е изд. — М. : БИНОМ. Лаборатория знаний
[2] Г. Нуссбаумер. Быстрое преобразование Фурье и алгоритмы вычисления сверток
[3] А.О. Лапаев Параллельное вычисление дискретного преобразования Фурье полинома в простом поле