Участник:Y.ryabkova/Умножение матриц методом Штрассена

Основные авторы описания: Ю.В.Рябкова

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Алгоритм Штрассена, описанный в 1969 году Фолькером Штрассеном, предназначен для умножения двух произвольных матриц при условии согласованности их размеров. В данном варианте алгоритма будет рассмотрен только частный случай умножения квадратных матриц порядка [math]n[/math] над полем вещественных чисел [math]\mathbb{R}[/math].

В 1965 году Штрассен нашел способ умножения двух матриц размера [math]2 \times 2[/math] с использованием семи умножений, в то время как классический алгоритм перемножения матриц требует восьми умножений. Стоит отметить, что данный способ не использует свойство коммутативности для операции перемножения чисел.

Теперь предположим, что [math]n = 2^L[/math], [math] L \in \mathbb{N} [/math] (далее будет показано, что это предположение не нарушает общности рассуждений), и будем рассматривать матрицы [math]A[/math] и [math]B[/math] как блочные [math]2 \times 2[/math]-матрицы с размером блоков [math]\frac{n}{2} \times \frac{n}{2} [/math]. Так как для блочных матриц правила умножения остаются теми же, как если бы на месте блока стояло число, а в методе Штрассена умножения [math]2 \times 2[/math]-матриц не используется коммутативность, этот метод подходит и для умножения блочных [math]2 \times 2[/math]-матриц. Таким образом, от задачи умножения [math]2 \times 2[/math]-матриц с семью умножениями можно перейти к задаче умножения [math]n \times n[/math]-матриц, требующей не более чем [math] O(7n^{\log_27}) [/math] операций, что асимптотически лучше классического способа умножения матриц сложностью [math]O(n^3)[/math]. На данный момент известны и более быстрые методы умножения матриц, однако алгоритм Штрассена относительно прост в реализации и эффективен на плотных матрицах не очень больших размеров, поэтому всё ещё широко используется.

1.2 Математическое описание алгоритма

Пусть [math] A, B \in \mathbb{R}^{n \times n} [/math] — заданные плотные матрицы. Вычислим матрицу [math] C \in \mathbb{R}^{n \times n} [/math], такую, что [math] C = AB [/math].

Для удобства будем полагать, что [math] n = 2^L, L \in \mathbb{N} [/math]. Это предположение не ограничивает общности рассуждений, так как если это свойство не выполнено и [math] n \lt 2^L [/math], можно рассмотреть квадратные матрицы [math]\tilde{A}[/math] и [math]\tilde{B}[/math] порядка [math] 2^L [/math] следующего вида:

[math] \tilde{A} = \begin{bmatrix} A & 0 \\ 0 & 0 \end{bmatrix}, \: \: \tilde{B} = \begin{bmatrix} B & 0 \\ 0 & 0 \end{bmatrix}, [/math]

то есть матрицы, полученные из матриц [math] A [/math] и [math] B [/math] дополнением их нулевыми строками и столбцами в позициях [math] i = \overline{n+1, 2^L} [/math] до размера [math] 2^L \times 2^L [/math]. По правилу перемножения блочных матриц:

[math] \tilde{C} = \tilde{A}\tilde{B} = \begin{bmatrix} AB & 0 \\ 0 & 0 \end{bmatrix} = \begin{bmatrix} C & 0 \\ 0 & 0 \end{bmatrix}. [/math]

Таким образом, решая задачу для матриц [math] \tilde{A} [/math] и [math]\tilde{B} [/math], получим решение исходной задачи умножения матриц [math] A [/math] и [math] B [/math] как левый верхний [math]n \times n[/math]-блок матрицы [math]\tilde{C}[/math]. Аналогичным образом можно не ограничивая общности предположить, что [math] n = s \cdot 2^L, \: L, s \in \mathbb{N} [/math].

Итак, пусть [math] n = 2^L, L \in \mathbb{N} [/math]. Рассмотрим матрицы [math] A [/math] и [math] B [/math] как блочные [math] 2 \times 2 [/math]-матрицы с квадратными блоками порядка [math]\frac{n}{2}[/math]:

[math] A = \begin{bmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{bmatrix}, \: \: B = \begin{bmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{bmatrix}. [/math]

Их произведение [math] C = AB [/math], согласно алгоритму Штрассена, вычисляется следующим образом:

[math] \begin{align*} &S_{1} = A_{11} + A_{22}, & &T_{1} = B_{11} + B_{22}, \\ &S_{2} = A_{21} + A_{22}, & &T_{2} = B_{11}, \\ &S_{3} = A_{11}, & &T_{3} = B_{12} − B_{22}, \\ &S_{4} = A_{22}, & &T_{4} = B_{21} − B_{11}, \\ &S_{5} = A_{11} + A_{12}, & &T_{5} = B_{22}, \\ &S_{6} = A_{21} − A_{11}, & &T_{6} = B_{11} + B_{12}, \\ &S_{7} = A_{12} − A_{22}, & &T_{7} = B_{21} + B_{22}, \end{align*} [/math]

[math] \alpha_{i} = S_{i} \cdot T_{i}, \: i = \overline{1,7}, [/math]

[math] C_{11} = \alpha_{1} + \alpha_{4} - \alpha_{5} + \alpha_{7}, [/math]

[math] C_{12} = \alpha_{3} + \alpha_{5}, [/math]

[math] C_{21} = \alpha_{2} + \alpha_{4}, [/math]

[math] C_{22} = \alpha_{1} + \alpha_{3} - \alpha_{2} + \alpha_{6}, [/math]

[math] C = \begin{bmatrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{bmatrix}.[/math]

Для вычисления матриц [math] \alpha_{i}, i = \overline{1,7} [/math], также требуется выполнить семь матричных умножений по формулам, данным выше, но уже для матриц порядка [math] \frac{n}{2} [/math]. Таким образом, получаем рекурсивный алгоритм, на каждом шаге рекурсии требующий семи умножений и сводящий задачу размера [math]k[/math] к задаче размера [math]\frac{k}{2}[/math]. Всего потребуется [math]\log_{2}n[/math] рекурсивных шагов, на последнем из которых задача будет сведена к перемножению двух чисел. Однако, на практике разумно продолжать рекурсивный процесс до тех пор, пока [math]k[/math] не станет достаточно малым (или, в случае [math] n = s \cdot 2^L [/math], пока [math]k[/math] кратно 2), а далее использовать классический способ умножения матриц. Именно такой вариант метода рассматривается в данном описании. Это связано с тем, что на малых матрицах алгоритм Штрассена теряет эффективность в сравнении с классическим алгоритмом умножения матриц, так как требует большого числа сложений.

Итак, пусть весь процесс перемножения матриц требует [math] m+1 [/math] рекурсивных шагов, где первые [math] m [/math] шагов выполняются в соответствии с алгоритмом Штрассена, а на последнем шаге используется классический алгоритм умножения матриц.

1.3 Вычислительное ядро алгоритма

В описанном алгоритме можно выделить два вычислительных ядра: первое соответствует операциям, выполняемым на первых [math] m [/math] рекурсивных шагах, а второе - последнему рекурсивному шагу с номером [math] m + 1[/math].

Вычислительное ядро последовательного варианта алгоритма Штрассена на каждом рекурсивном шаге, кроме последнего, можно составить из вычисления матриц [math] S_{i}, T_{i}, \: i = \overline{1, 7} [/math], и блоков матрицы [math] C [/math] из матриц [math] \alpha_{i}, \: i = \overline{1, 7} [/math] по формулам, данным в математическом описании алгоритма. Все эти вычисления представляют из себя сложения (вычитания) матриц порядка [math] k [/math], зависящего от номера шага [math] s_m [/math] следующим образом: [math] k = \frac{n}{2^{s_m}} [/math]. Операции выполняются поэлементно. Таким образом, первое вычислительное ядро алгоритма сводится к операциям сложения (вычитания) чисел на каждом рекурсивном шаге.

Вычислительное ядро алгоритма на последнем, [math] m+1 [/math]-ом рекурсивном шаге, состоит из операций перемножения двух матриц по классическому алгоритму кубической сложности, основную часть которого составляют умножения чисел.

Указанные операции составляют основную часть метода, причем с увеличением [math] m [/math] доля операций первого вычислительного ядра будет расти, а доля операций второго - падать, и наоборот.

1.4 Макроструктура алгоритма

Алгоритм Штрассена состоит из [math] m+1 [/math] рекурсивных шагов и может быть представлен в виде двух этапов.

Первый этап соответствует первым [math] m [/math] рекурсивным шагам, на каждом из которых можно выделить следующие три последовательные макрооперации:

• вычисление матриц [math] S_{i}, T_{i}, \: i = \overline{1, 7} [/math];

• рекурсивный вызов для вычисления произведений [math] \alpha_{i} = S_{i} \cdot T_{i}, \: i = \overline{1, 7} [/math], таким образом при переходе на следующий рекурсивный шаг задача размера [math] k [/math] сводится к семи задачам размера [math] \frac{k}{2} [/math];

• вычисление матрицы [math] C [/math] из матриц [math] \alpha_{i} [/math].

Второй этап соответствует последнему, [math] m+1 [/math]-ому шагу алгоритма и выходу из рекурсии. Он представляет из себя вычисление произведения двух матриц матриц порядка [math] n_{m} = \frac{n}{2^{m}} [/math] по классическому алгоритму:

[math] c_{ij} = \sum_{k = 1}^{n_{m}} a_{ik} b_{kj}, \: i,j = \overline{1, n_{m}} [/math].

1.5 Схема реализации последовательного алгоритма

Псевдокод простейшего варианта реализации последовательного алгоритма Штрассена, непосредственно вытекающего из его математического описания, может быть записан следующим образом:

	Strassen(A, B, C, k, m) ! C = A * B
           if (m == 0) call mul(A, B, C, k) ! переход к классическому алгоритму умножения матриц
           do i = 1, 7
               compute S[i], T[i] from A and B
           end do
           do i = 1, 7
               call Strassen(S[i], T[i], alpha[i], k/2, m-1)
           end do
           do i = 1, 7
               compute parts of C from alpha[i]
           end do
        end Strassen

Таким образом, на каждом рекурсивном шаге эта схема состоит из трёх последовательных этапов:

• Вычисление семи пар матриц [math] S_{i}, T_{i} [/math]. Так как они определены независимо друг от друга и хранятся в разных областях памяти, порядок их вычисления может быть произвольным, в том числе параллельным.

• Выполнение семи рекурсивных вызовов функции Strassen, по одному для каждой тройки [math] \alpha_{i} = S_{i} \cdot T_{i}[/math]. Порядок этих вызовов также может быть произвольным и параллельным.

• Вычисление матрицы [math] С [/math] из полученных после рекурсивных вызовов матриц [math] \alpha_{i} [/math].

Как видно, данная реализация требует большого количества дополнительной памяти, так как на каждом рекурсивном шаге необходимо одновременно хранить семь пар [math]\frac{k}{2}\times\frac{k}{2}[/math]-матриц [math] S_{i}, T_{i} [/math] и семь результатов их умножения [math] \alpha_{i} [/math].

Есть и другой вариант реализации последовательного алгоритма, позволяющий значительно сократить количество требуемой памяти:

	Strassen(A, B, C, k, m) ! C = A * B
           if (m == 0) call mul(A, B, C, k) ! переход к классическому алгоритму умножения матриц
           do i = 1, 7
               compute S[i], T[i] from A and B
               call Strassen(S[i], T[i], alpha[i], k/2, m-1)
               compute part of C from alpha[i]
           end do
        end Strassen

На каждом рекурсивном шаге схема этой реализации представляет собой цикл по [math]i = 1,\dotsc,7[/math], каждая итерация которого состоит из трёх последовательных этапов:

• Вычисление [math]i[/math]-ой пары матриц [math] S_{i}, T_{i} [/math].

• Выполнение рекурсивного вызова функции Strassen для вычисления [math] \alpha_{i} = S_{i} \cdot T_{i} [/math].

• Обновление блоков матрицы [math] С [/math] в соответствии с формулами алгоритма в зависимости от номера полученной после рекурсивного вызова матрицы [math] \alpha_{i} [/math].

Порядок итераций такого цикла может быть произвольным, но они должны выполняться строго последовательно. Такое требование позволяет выделить память всего для трёх [math]\frac{k}{2}\times\frac{k}{2}[/math]-матриц на каждом рекурсивном шаге: для одной пары [math] S_{i}, T_{i} [/math] и их произведения [math] \alpha_{i} [/math], и на каждой итерации цикла использовать одни и те же области памяти для хранения соответствующей тройки матриц.

1.6 Последовательная сложность алгоритма

Оба вышеописанных варианта реализации метода Штрассена требуют одинакового числа арифметических операций. В соответствии с макроструктурой алгоритма, рассмотрим каждый из его двух этапов отдельно.

Первый этап требует на первом рекурсивном шаге выполнения [math]18 \left( \frac{n}{2} \right)^2 [/math] сложений (вычитаний). При переходе на следующий рекурсивный шаг, задача будет сведена к семи аналогичным задачам, но вдвое меньшей размерности. Отсюда получаем, что на [math]k[/math]-ом шаге потребуется [math]18 \cdot 7^{k-1} \left( \frac{n}{2^{k}} \right)^2 [/math] операций. Тогда всего на первых [math] m [/math] шагах потребуется следующее число сложений (вычитаний):

[math] 18 \left( \frac{n}{2} \right)^2 + 18 \cdot 7 \left( \frac{n}{4} \right)^2 + \dotsb + 18 \cdot 7^{m-1} \left( \frac{n}{2^{m}} \right)^2 = \frac{18}{4}n^{2}\left( 1 + \frac{7}{4} + \dotsb + \frac{7^{m-1}}{4^{m-1}}\right) = 6n^2\left(\frac{7^{m}}{4^{m}} - 1 \right) [/math].

Получена сложность первого этапа алгоритма.

Второй этап включает в себя решение [math]7^m[/math] задач перемножения матриц порядка [math] \frac{n}{2^{m}} [/math] по классическому алгоритму, что требует [math]7^m \left(\frac{n}{2^{m}}\right)^3[/math] умножений и [math]7^m \left(\frac{n}{2^{m}}\right)^2\left(\frac{n}{2^{m}}-1\right)[/math] сложений, всего [math]O\left(\frac{n^3}{2^{3m}}\right)[/math] арифметических операций.

Всего последовательный алгоритм Штрассена требует:

• [math]6n^2\left(\frac{7^{m}}{4^{m}} - 1 \right) + 7^m\left(\frac{n}{2^{m}}\right)^2\left(\frac{n}{2^{m}}-1\right)[/math] сложений;
• [math]7^m\left(\frac{n}{2^{m}}\right)^3[/math] умножений.

Как видно, сложность алгоритма зависит не только от порядка матрицы [math] n [/math], но и от числа [math] m [/math] рекурсивных шагов первого этапа.

Если [math] m = L[/math], где [math]n = 2^L[/math], то есть второй этап алгоритма сводится лишь к [math]7^L[/math] умножениям двух чисел, то сложность всего последовательного алгоритма равна

[math] 6n^2\left(\frac{7^{L}}{4^{L}} - 1 \right) + 7^L\left(\frac{n}{2^{L}}\right)^3 = 6n^2\left(\frac{7^{L}}{n^{2}} - 1 \right) + 7^L = 7 \cdot 7^{L} - 6n^2 = 7 n^{\log_2 7} - 6n^2 = O\left(n^{\log_2 7}\right) \approx O\left(n^{2.81}\right) [/math].

Таким образом, получена оценка сложности последовательного алгоритма Штрассена с максимально возможным числом [math]m = L[/math] рекурсивных шагов, соответствующая максимальной оценке сложности первого этапа алгоритма для произвольного [math]m[/math]. Эта оценка асимптотически лучше оценки для классического метода перемножения матриц, требующего [math]O(n^3)[/math] операций.

Стоит отметить роль правильного выбора параметра [math] m [/math]. Из полученных оценок видно, что при малых [math] m [/math] сложность алгоритма с уменьшением этого параметра будет стремиться к кубической сложности классического метода, а значит [math] m [/math] стоит выбирать относительно близким к [math] L [/math]. Однако, при [math] m [/math], очень близких к [math] L [/math], алгоритм на последних рекурсивных шагах будет применяться на матрицах малых размеров и требовать большего числа сложений, чем классический метод, и эта разница будет увеличиваться с уменьшением размера матрицы, что соответствует увеличению [math] m [/math]. Отсюда следует, что существует некоторое оптимальное значение [math] m \in [1, L] [/math], которое минимизирует число арифметических операций всего алгоритма и выбирается исходя из минимального размера матрицы, на которой описанный в первом этапе рекурсивный алгоритм будет эффективнее классического. Также при выборе [math] m [/math] стоит учитывать роль накладных расходов на реализацию рекурсии при малых размерах матриц.

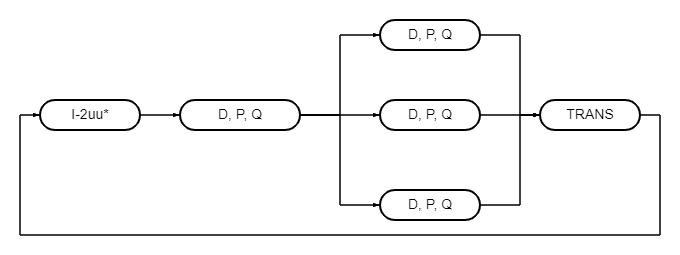
1.7 Информационный граф

Граф алгоритма зависит от параметра [math] m [/math], то есть от заданного числа рекурсивных шагов. На рисунке изображен граф при [math] m = 1 [/math], отражающий макроструктуру алгоритма (первая схема реализации последовательного алгоритма).

Рисунок 1. Операции в последовательном алгоритме Штрассена при m = 1. Вершина mul() означает вызов классического метода умножения матриц.

Как видно, на каждом уровне все операции могут выполняться параллельно и независимо друг от друга. При увеличении [math] m [/math] на единицу, число уровней будет увеличиваться на два. Например, на данном графе это означает, что после вычисления всех [math] S_{i}, T_{i} [/math] из входных данных [math] A, B[/math] будут производиться аналогичные вычисления для каждой пары [math] S_{i}, T_{i} [/math]. Таким образом, новый уровень графа будет содержать [math]2 \cdot 49[/math] макроопераций. Из аналогичных соображений после вызовов mul() из возвращаемых значений надо будет сначала вычислить [math] \alpha_{i} [/math] (семь независимых макроопераций), а уже из этих значений получить матрицу [math] С [/math].

1.8 Ресурс параллелизма алгоритма

Для реализации параллельного варианта алгоритма Штрассена небходимо последовательно выполнить следующие ярусы:

• [math] m [/math] ярусов вычисления матриц [math] S_{i}, T_{i} [/math] порядка [math]\frac{n}{2^k}[/math], где [math]k[/math] - номер яруса. Сложность этого этапа равна [math] \frac{n^2}{3}\left(1-\frac{1}{4^m}\right) [/math] операциям сложения.
• Ярус алгоритма классического умножения для матриц порядка [math] \frac{n}{2^{m}} [/math], что требует [math]\left(\frac{n}{2^{m}}\right)^3[/math] умножений и [math]\left(\frac{n}{2^{m}}\right)^2\left(\frac{n}{2^{m}}-1\right)[/math] сложений.
• [math] m [/math] последовательных ярусов вычисления матрицы произведения [math]C[/math] из полученных на предыдущем шаге матриц [math]\alpha_{i}[/math]. Сам процесс вычисления этой матрицы можно разбить на четыре параллельных и независимых вычисления её блоков (исходя из формул математического описания алгоритма), поэтому сложность всего этапа составит [math] n^2 \left(1-\frac{1}{4^m}\right) [/math].

Таким образом, сложность всего параллельного алгоритма составит [math]\frac{4 n^2}{3}\left(1-\frac{1}{4^m}\right) + \left(\frac{n}{2^{m}}\right)^3 + \left(\frac{n}{2^{m}}\right)^2\left(\frac{n}{2^{m}}-1\right) [/math] арифметических операций. При [math]m[/math], близких к [math]L[/math], эта оценка равна [math]O(n^2)[/math], то есть параллельная версия алгоритма Штрассена имеет квадратичную сложность.

Основной ресурс конечного параллелизма алгоритма - независимое вычисление матриц [math] S_{i}, T_{i} [/math] на каждом рекурсивном шаге, причем с каждым шагом их количество возрастает в семь раз. Аналогично, при выходе из рекурсии, вычисление матриц-произведений из [math]\alpha_{i}[/math] производится независимо, причем вычисление каждой из них представимо в виде независимого обновления её четырех блоков.

Более того, можно распараллелить вычисление каждой из матриц [math] S_{i}, T_{i} [/math], так как оно сводится к операции сложения матриц, а значит к независимым операциям сложения элементов или блоков матрицы.

1.9 Входные и выходные данные алгоритма

Входные данные: матрицы [math]A[/math] и [math]B[/math] порядка [math] n [/math], где, в общем случае, [math] n = s \cdot 2^L[/math]. В данной реализации алгоритма в силу блочно-параллельного выполнения операции сложения двух матриц и особенностей их хранения, дополнительно требуется [math] n = s \cdot 7^{\left[\frac{\log_7p+1}{2}\right]} \cdot 2^m[/math], где [math]p[/math] - число процессов.

Объём входных данных: [math]n^2 + n^2[/math].

Выходные данные: матрица [math]C[/math].

Объём выходных данных: [math]n^2[/math].

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Проведём исследование масштабируемости параллельной реализации алгоритма Штрассена. Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета. Изменяемые параметры запуска реализации:

• число процессоров: 1, 7, 49, 343,
• размер матрицы: 14, 28, 56, 112, 224, 392, 448, 784, 896, 1568, 1792, 3136, 3584, 6272, 7168, 12544, 14336.

На следующем рисунке приведен график производительности реализованного алгоритма при фиксированной вычислительной сложности задачи.

Рисунок 2. График производительности алгоритма Штрассена

Видно, что с увеличением числа процессоров производительность растет, однако отношение ее прироста к увеличению числа процессоров значительно меньше единицы.

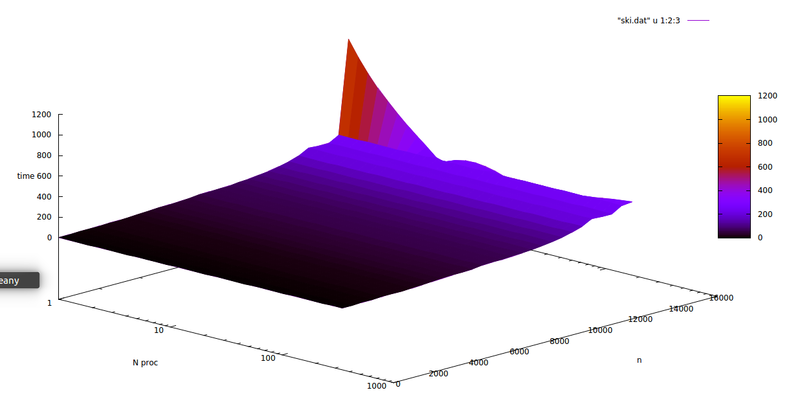
Следующий график показывает время работы алгоритма для различных входных параметров.

Рисунок 3. График времени работы алгоритма Штрассена

Время работы программы резко возрастает на больших матрицах при малом числе процессоров.