Участник:ZhenyaNikishkina/Перемножение разреженных матриц
| Умножение разреженных матриц | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(mnl)[/math] |
| Объём входных данных | [math]mn+3+nl+3[/math] |
| Объём выходных данных | [math]ml+5[/math] |
Основные авторы описания: Е.Г.Никишкина
В численном анализе и научных вычислениях разреженная матрица - это матрица, в которой большинство элементов равны нулю.[1] Не существует строгого определения доли элементов с нулевым значением для того, чтобы матрица считалась разреженной, но общим критерием является то, что количество ненулевых элементов примерно равно количеству строк или столбцов. Напротив, если большинство элементов ненулевые, матрица считается плотной.[1] Число элементов с нулевым значением, деленное на общее количество элементов (например, m × n для матрицы m × n), иногда называют разреженностью матрицы.
Концептуально разреженность соответствует системам с небольшим количеством попарных взаимодействий. Например, рассмотрим линию шариков, соединенных пружинами от одного к другому: это разреженная система, поскольку соединены только соседние шарики. Напротив, если бы одна и та же линия шариков имела пружины, соединяющие каждый шарик со всеми остальными шариками, система соответствовала бы плотной матрице. Концепция разреженности полезна в комбинаторике и прикладных областях, таких как теория сетей и численный анализ, которые обычно имеют низкую плотность значимых данных или соединений. Большие разреженные матрицы часто появляются в научных или инженерных приложениях при решении уравнений в частных производных. Разреженные матрицы встречаются при решении многих важных практических задач: структурного анализа, в теории графов, теории электрических сетей и энергосистем распределения энергии[2], при численном решении дифференциальных уравнений, математической физики, строительной механики, механики конструкций летательных и иных аппаратов; при прогнозировании метеорологических и гидрогеологических процессов[3]; при обеспечении работы графических процессоров[4], а также при изучении статического равновесия физических, технических, биологических, производственно-экономических и других типов систем.[5]
При хранении разреженных матриц и манипулировании ими на компьютере полезно и часто необходимо использовать специализированные алгоритмы и структуры данных, которые используют преимущества разреженной структуры матрицы. Для разреженных матриц были созданы специализированные компьютеры[6], поскольку они широко распространены в области машинного обучения.[7] Операции, использующие стандартные структуры и алгоритмы с плотной матрицей, являются медленными и неэффективными при применении к большим разреженным матрицам, поскольку обработка и память тратятся впустую на нули. Разреженные данные по своей природе легче сжимаются и, следовательно, требуют значительно меньшего объема памяти. Некоторыми очень большими разреженными матрицами невозможно манипулировать с помощью стандартных алгоритмов с плотной матрицей.
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
Пусть дана разреженная матрица [math]A[/math] = [math]\begin{pmatrix} 0 & 6 & 0 & 0 \\ 4 & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 7 & 0 & 1 \\ \end{pmatrix}[/math]
Существует несколько типов хранения разреженных матриц, которые позволяют оптимально использовать память и ускорить выполнение операций. Некоторые из наиболее популярных методов хранения разреженных матриц включают:
1. Список списков (List of Lists, LIL): В этом представлении разреженной матрицы каждая строка матрицы хранится в виде списка, содержащего пары (индекс столбца, значение). Этот формат удобен для построения и модификации разреженных матриц, но может быть неэффективным для матричных операций.
LIL (List of Lists) представление будет выглядеть следующим образом:
LIL(A) = [
[(1, 6)], # ненулевой элемент в 1-й строке - 6 во 2-м столбце
[(0, 4)], # ненулевой элемент в 2-й строке - 4 в 1-м столбце
[(2, 2)], # ненулевой элемент в 3-й строке - 2 в 3-м столбце
[(1, 7), (3, 1)] # ненулевые элементы в 4-й строке - 7 во 2-м столбце, 1 в 4-м столбце
]
2. Сжатое представление по строкам (Compressed Sparse Row, CSR) / Сжатое представление по столбцам (Compressed Sparse Column, CSC): В CSR и CSC форматах разреженная матрица представляется с помощью трех одномерных массивов: значения (non-zero values), индексы столбцов (column indices) и указатели на начало каждой строки (row pointers) для CSR или указатели на начало каждого столбца (column pointers) для CSC. Эти форматы являются наиболее распространенными и эффективными для матричных операций, таких как сложение, умножение и транспонирование.
CSR (Compressed Sparse Row) представление будет выглядеть следующим образом:
values = [6, 4, 2, 7, 1]
column_indices = [1, 0, 2, 1, 3]
row_pointers = [0, 1, 2, 3, 5]
CSC (Compressed Sparse Column) представление для этой же матрицы будет таким:
values = [4, 6, 7, 2, 1]
row_indices = [1, 0, 3, 2, 3]
column_pointers = [0, 1, 3, 4, 5]
3. Координатный формат (COO, Coordinate List): В координатном формате каждый ненулевой элемент матрицы представляется с помощью трех значений: индекс строки, индекс столбца и значение элемента. Этот формат удобен для добавления и изучения элементов, но менее эффективен для выполнения матричных операций по сравнению с CSR и CSC.
COO (Coordinate List) представление:
row_indices = [0, 1, 2, 3, 3]
column_indices = [1, 0, 2, 1, 3]
values = [6, 4, 2, 7, 1]
4. Диагональное представление (DIA, Diagonal Storage): В этом формате хранятся только диагонали матрицы, содержащие хотя бы одно ненулевое значение. Это достигается путем хранения значений диагоналей в двумерном массиве и массива смещений для каждой диагонали. DIA подходит для матриц с преимущественно диагональными элементами, например, для тридиагональных матриц, встречающихся при решении уравнений методом прогонки.
DIA (Diagonal Storage) представление: Поскольку матрица A содержит 4 диагонали с ненулевыми элементами, DIA представление будет включать только их:
Диагональ с индексом 1 (диагональ выше главной): [6, 0, 0];
Диагональ с индексом 0 (главная диагональ): [0, 0, 2, 1];
Диагональ с индексом -1 (диагональ ниже главной): [4, 0, 0];
Диагональ с индексом -2 (диагональ ниже главной): [0, 7].
diagonals = [math]\begin{pmatrix} * & * & 0 & * \\ * & 4 & 0 & 6 \\ 0 & 0 & 2 & 0 \\ 7 & 0 & 1 & 0 \\ \end{pmatrix}[/math]
offsets = [math]\begin{pmatrix} -2 & -1 & 0 & 1 \end{pmatrix}[/math]
Здесь diagonals - двумерный массив значений диагоналей матрицы [math] A[/math] . Порядок следования диагоналей в массиве выбирается произвольно. offsets - одномерный массив, который указывает смещение каждой диагонали относительно главной диагонали. Положительные значения указывают на диагонали, расположенные выше главной, отрицательные значения - ниже главной.
5. ELLPACK / ITPACK представление (ELLPACK / ITPACK, ELL): В ELLPACK / ITPACK формате каждая строка матрицы представлена вектором фиксированной длины, содержащим значения и индексы столбцов L наиболее длинных строк, остальные элементы дополняются нулями. Это делает этот формат легко параллелизуемым на графических процессорах, но он может быть неэффективным, если разница в количестве ненулевых элементов между самой длинной и самой короткой строками слишком велика.
ELLPACK / ITPACK (ELL) представление определяется с использованием фиксированной длины массивов для строк матрицы. В данной матрице максимальное количество ненулевых элементов в строках равно 2 (для строки 4). Будем использовать массивы длины 2.
indices = [math]\begin{pmatrix} 1 & -1 \\ 0 & -1 \\ 2 & -1 \\ 1 & 3 \\ \end{pmatrix}[/math]
values = [math]\begin{pmatrix} 6 & 0 \\ 4 & 0 \\ 2 & 0 \\ 7 & 1 \\ \end{pmatrix}[/math]
Здесь indices - двумерный массив, в котором каждая строка содержит индексы столбцов ненулевых элементов соответствующей строки матрицы [math]A[/math]. Если количество ненулевых элементов в строке меньше, чем максимальное количество для других строк, то оставшиеся значения дополняются специальным индексом(обычно -1). values - двумерный массив такой же структуры, как и массив indices, но он содержит сами ненулевые значения элементов матрицы [math]A[/math]. Если строка содержит менее максимального количества ненулевых элементов, то оставшиеся значения в строке дополняются нулями.
Выбор подходящего формата хранения разреженной матрицы зависит от решаемой задачи, преимущественно используемых операций и требований к производительности.
1.1 Общее описание алгоритма
Перемножение разреженных матриц - одна из задач в алгоритмах линейной алгебры, широко применяющаяся в различных методах. Здесь мы рассмотрим умножение [math]C = AB[/math] разреженных матриц (последовательный вещественный вариант). В реализации алгоритма умножения матриц, формат хранения разреженных матриц играет существенное значение для обеспечения эффективной производительности и оптимального использования ресурсов.
1.2 Математическое описание алгоритма
Формулы для перемножения матриц не зависят от их форматов, и операция умножения матриц всегда основана на стандартной формуле умножения матриц. Исходные данные: разреженная матрица [math]A[/math] (элементы [math]a_{ij}[/math]), разреженная матрица [math]B[/math] (элементы [math]b_{ij}[/math]).
Вычисляемые данные: разреженная матрица [math]C[/math] (элементы [math]c_{ij}[/math]).
Формулы метода:
- [math] \begin{align} c_{ij} = \sum_{k = 1}^{n} a_{ik} b_{kj}, \quad i \in [1, m], \quad j \in [1, l]. \end{align} [/math]
1.3 Вычислительное ядро алгоритма
Вычислительное ядро перемножения разреженных неособенных матриц можно составить из множественных (всего их [math]l[/math]) вычислений умножения матрицы [math]A[/math] на столбцы матрицы [math]B[/math], или (при более детальном рассмотрении), из множественных (всего их [math]ml[/math]) скалярных произведений строк матрицы [math]A[/math] на столбцы матрицы [math]B[/math]:
- [math]\sum_{k = 1}^{n} a_{ik} b_{kj}.[/math]
1.4 Макроструктура алгоритма
Как уже записано в описании ядра алгоритма, основную часть умножения матриц составляют множественные (всего [math]ml[/math]) вычисления скалярных произведений строк матрицы [math]A[/math] на столбцы матрицы [math]B[/math]
- [math]\sum_{k = 1}^{n} a_{ik} b_{kj}.[/math]
1.5 Схема реализации последовательного алгоритма
Для матричного умножения интуитивно понятно, что представление, которое может обеспечить легкий доступ к элементам каждой строки матрицы [math]A[/math] и элементам каждого столбца матрицы [math]B[/math], является идеальным способом реализации данной процедуры. Форматы CSR и CSC естественным образом индексируют элементы в виде строк и столбцов соответственно, и при использовании в сочетании друг с другом удовлетворяют данное требование. Рассмотрим матицы [math]A[/math] и [math]B[/math]: первая представлена в формате CSR, вторая представлена в формате CSC.
- Инициализировать
totalcountравным 0. - Выделить память для массива
result_localс размером, равным числу строкmatrix.rows. - Инициализировать массив
result_localнулевым количеством просмотренных элементов в каждой строке и выделить память для массивов его элементов. - Ввести распараллеленный цикл (с помощью OpenMP) по строкам первой матрицы.
- Для каждой строки
iвычислить количество ненулевых элементов в строке из первой матрицы, которая представлена в формате CSR. - Для каждого столбца
jвторой матрицы, представленной в формате CSC, выполнить следующие действия:- Инициализировать
dp(скалярное произведение) равным 0. - Установить
m1posв качестве начального индекса строкиi, аm1seen- в 0. - Вычислить количество ненулевых элементов в столбце
j(m2count) и установить дляm2posначальный индекс столбцаj, а дляm2seen- 0. - Выполнить итерацию по ненулевым элементам строки
iи столбцаj, умножая совпадающие элементы и суммируя их вdp. - Если
dpне равно 0, сохранить результат вresult_local[i].elements.
- Инициализировать
- После каждой итерации
iобновлятьtotalcountколичеством ненулевых элементов изresult_local[i]. - После завершения параллельного цикла инициализировать результирующую матрицу
resultв формате COO соответствующими значениями и выделить память для массива ее элементов. - Скопировать ненулевые элементы из
result_localвresult.elementsи освободить память, выделенную дляresult_local. - Вернуть результирующую матрицу в формате COO, содержащую произведение двух входных матриц.
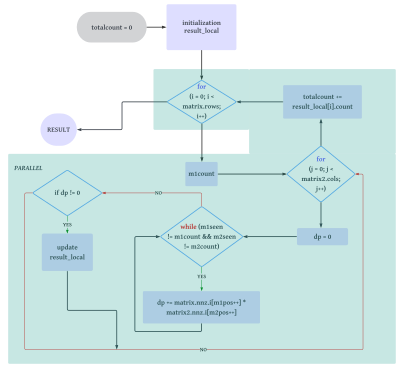
Граф представляет шаги, описанные в виде последовательности операций с точками принятия решения и параллельной обработкой, указанными для цикла на шаге 4. Описанный граф изображен на рис. 1.
1.6 Последовательная сложность алгоритма
в наихудшем случае для каждого элемента [math]A[/math] выполняется точечное произведение на каждый элемент [math]B[/math], что приводит к временной сложности [math]O(mnl)[/math], где [math]m, n[/math] - количество строк в [math]A[/math], [math]B[/math] соответственно, а [math]l[/math] - количество столбцов в [math]B[/math]. Добавление кода постобработки, необходимого для обеспечения параллелизма, требует в худшем случае [math]O(ml)[/math] времени, чтобы объединить локальные результаты вместе. Следовательно, общая сложность в худшем случае равна [math]O(mnl + ml)[/math]. В случае разреженных матриц временная сложность составляет [math]O(P(sparse)mnl)[/math], где [math]P(sparse)[/math] - вероятность того, что элемент будет ненулевым. Хотя временная сложность постобработки, требуемая для параллелизма, может показаться огромной, [math]O(ml)[/math], в общей сложности процедуры доминирует ее полиномиальный член [math]mnl[/math].
1.7 Информационный граф
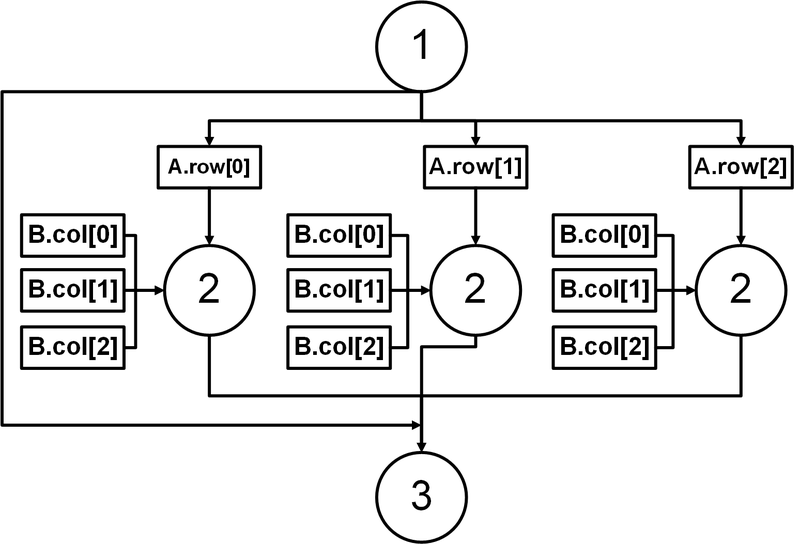
На рис. 2 изображен информационный граф алгоритма перемножения разреженных матриц. Этапы выполнения метода помечены цифрами:
1 - инициализация результата;
2 - параллельное вычисление скалярного произведения;
3 - объединение полученных результатов.
На этапе 2 параллельно для каждой строки считается скалярное произведение. При этом в каждом потоке доступ к столбцам второй матрицы осуществляется последовательно.
1.8 Ресурс параллелизма алгоритма
Для обеспечения возможности реализации параллельных вычислений потребовались изменения в коде процедуры. До модификации процедура выполняла бы два цикла for для вычисления искомого скалярного произведения между ненулевыми элементами каждой строки первой матрицы [math]A[/math] и ненулевыми элементами каждого столбца второй матрицы [math]B[/math]. Проблема заключалась в том, что каждая итерация использовала счетчик для вычисления индекса, по которому следующий элемент должен быть помещен в результирующую матрицу.
Модификация кода включала создание массива для временного хранения результирующих значений. Это устраняет зависимость, переносимую циклом, из этого счетчика. Модификация позволяет для нахождения результата на каждой итерации иметь доступ к своему собственному счетчику. В конце процедуры эти локальные результаты объединяются обратно в результирующую матрицу и освобождаются из памяти.
Объединение локальных копий результатов в формате CSR оказалось довольно неэффективным, поэтому был выбран формат COO. Каждому элементу требовались только координаты [math]x[/math] и [math]y[/math], которые были легко получены без каких-либо зависимостей. Объединение локальных результатов типа COO не было сложной задачей, поскольку они уже были естественным образом отсортированы. Для обеспечения параллелизма была использована следующая функция.
#pragma omp parallel for reduction(+:totalcount) shared(matrix,matrix2)
Данная директива используется в контексте OpenMP, который представляет собой API для многопоточного программирования на C, C++ и Fortran. Эта директива указывает компилятору на необходимость создания параллельной области, в которой цикл for будет выполняться несколькими потоками одновременно. Конкретное действие каждой части директивы можно объяснить следующим образом:
1. #pragma omp parallel: создает параллельную область, где следующие за этим кодом инструкции будут выполняться различными потоками одновременно.
2. for: указывает, что следующий за директивой цикл for должен быть распределен между потоками так, что каждый поток выполняет часть итераций цикла.
3. reduction(+:totalcount): определяет, что переменная totalcount будет использоваться для операции редукции с использованием оператора сложения. Для каждого потока будет создана локальная копия totalcount, и каждый поток будет обновлять свою копию, чтобы избежать состояния гонки. В случае, если бы использовалась одна переменная с результатом, то один из потоков после записи скалярного произведения в результат может не успеть увеличить переменную-счетчик до того, как какой-либо другой поток сделает запись в результат. В таком случае другой поток перепишет значение, созданное первоначальным потоком, и программа будет работать некорректно. После завершения всех итераций цикла значения из всех локальных копий будут сложены вместе, и их сумма будет сохранена в исходной переменной totalcount, обеспечивая тем самым корректный результат независимо от многопоточности.
4. shared(matrix,matrix2): указывает, что две входные матрицы matrix и matrix2 будут доступны всем потокам и что они разделяют общую память. Поскольку каждый поток может читать и/или записывать в эти массивы, необходимо обеспечить отсутствие состояния гонки.
В результате, при использовании этой директивы, код, следующий за ней, будет выполняться параллельно с разделением цикла for на порции для разных потоков, суммируя результат в переменную totalcount и с доступом каждого потока к общим данным в matrix и matrix2.
1.9 Входные и выходные данные алгоритма
Входные данные: матрица [math]A[/math] (элементы [math]a_{ij}[/math]), матрица [math]B[/math] (элементы [math]b_{ij}[/math]), для каждой из матриц количество строк и столбцов, а также тип данныx(int/float).
Объём входных данных: [math]mn+3+nl+3[/math]
Выходные данные: матрица [math]C[/math] (элементы [math]c_{ij}[/math]), количество строк и столбцов, тип данных, время считывания входных матриц и время выполнения операции умножения в секундах.
Объём выходных данных: [math]ml+5[/math]
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Проведём исследование масштабируемости параллельной реализации умножения разреженных матриц. Исследование проводилось на cуперкомпьютере "Ломоносов-2"[8].
Результаты экспериментов представлены на рис. 3 (для int) и рис. 4 (для float). Приведенные данные демонстрируют явное ускорение при выполнении процедуры в многопоточном режиме в отличие от однопоточного, причем с увеличением числа потоков эта разница увеличивается. Чтобы изучить это поведение более подробно, процедура была запущена на квадратных матрицах различного размера: [math]128 \times 128[/math], [math]512 \times 512[/math], [math]1024 \times 1024[/math], [math]4096 \times 4096[/math]. Для каждой из матриц наблюдается следующее: при увеличении числа потоков время выполнения операции сокращается. Также можно заметить, что время выполнения операции для матриц с элементами типа int и float практически не отличается.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
В настоящее время существуют несколько реализаций алгоритмов и библиотек для перемножения разреженных матриц. Вот некоторые из них:
1. SciPy (Python): SciPy - это библиотека с открытым исходным кодом для решения математических, научных и технических проблем. В этой библиотеке реализован класс "sparse", который предоставляет различные форматы разреженных матриц и эффективные методы перемножения для них. Документация SciPy для работы с разреженными матрицами доступна по ссылке.[9]
2. Eigen (C++): Eigen - это высокоуровневая C++ библиотека для линейной алгебры, с поддержкой перемножения разреженных матриц. Она предоставляет широкий набор функций и методов для удобной работы с разреженными матрицами. Документация Eigen по разреженной линейной алгебре доступна по ссылке.[10]
3. SuiteSparse (C): SuiteSparse - это набор связанных модулей с открытым исходным кодом для работы с разреженными матрицами. Она включает в себя несколько высокопроизводительных алгоритмов и пакетов, таких как UMFPACK, CHOLMOD, SPQR и многие другие, которые эффективно перемножают разреженные матрицы. Документация SuiteSparse доступна по ссылке.[11]
4. cuSPARSE (CUDA): cuSPARSE - это библиотека для работы с разреженными данными на графических процессорах с архитектурой NVIDIA CUDA. Она предоставляет функции для перемножения разреженных матриц, используя преимущества параллельных вычислений на GPU. Документация cuSPARSE доступна по ссылке.[12]
5. GraphBLAS (C): GraphBLAS - это C-библиотека для обработки больших графов и разреженных матриц. Она позволяет выполнять комплексные алгоритмы и анализ данных на высоком уровне абстракции, при этом используя эффективные алгоритмы перемножения разреженных матриц внутри пакета. Документация GraphBLAS доступна по ссылке.[13]
Это лишь несколько примеров реализаций алгоритмов перемножения разреженных матриц, доступных в различных языках программирования и фреймворках. В зависимости от требований можно выбрать любую из этих библиотек и использовать их функции для эффективного перемножения разреженных матриц.
3 Литература
- ↑ 1,0 1,1 Yan, Di; Wu, Tao; Liu, Ying; Gao, Yang (2017). "An efficient sparse-dense matrix multiplication on a multicore system". 2017 IEEE 17th International Conference on Communication Technology (ICCT). IEEE. pp. 1880–1883. doi:10.1109/icct.2017.8359956. ISBN 978-1-5090-3944-9.
- ↑ Тьюарсон Р. Разреженные матрицы. — М.: Мир, 1977.
- ↑ Брумштейн Ю. М, Использование псеводогидродинамической постановки в задачах фильтрации со свободной поверхностью // Естественные науки. Астрахань: Издательский дом «Астраханский университет». — 2004. — № 8. — С. 125–128.
- ↑ Dehnavi M. M., Fernández D. M., Giannacopoulos D. Finite-element sparse matrix vector multiplication on graphic processing units // IEEE Transactions on Magnetics. — 2010. — Vol. 46, № 8. — P. 2982–2985.
- ↑ Солнцева М. О., Кухаренко Б. Г. Применение методов кластеризации узлов на графах с разреженными матрицами смежности в задачах логистики // Труды МФТИ. — 2013. — Т. 5, № 3 (19). — С. 75–83.
- ↑ Cerebras Systems Unveils the Industry's First Trillion Transistor Chip
- ↑ Argonne national laboratory deploys cerebras cs1 the worlds fastest artificial intelligence computer
- ↑ Суперкомпьютерный комплекс МГУ, включая суперкомпьютер "ЛОМОНОСОВ-2"
- ↑ Документация SciPy.
- ↑ Документация Eigen.
- ↑ Документация SuiteSparse.
- ↑ Документация cuSPARSE.
- ↑ Документация GraphBLAS