Complete cyclic reduction, locality
Содержание
1 Ссылки
2 Локальность данных и вычислений
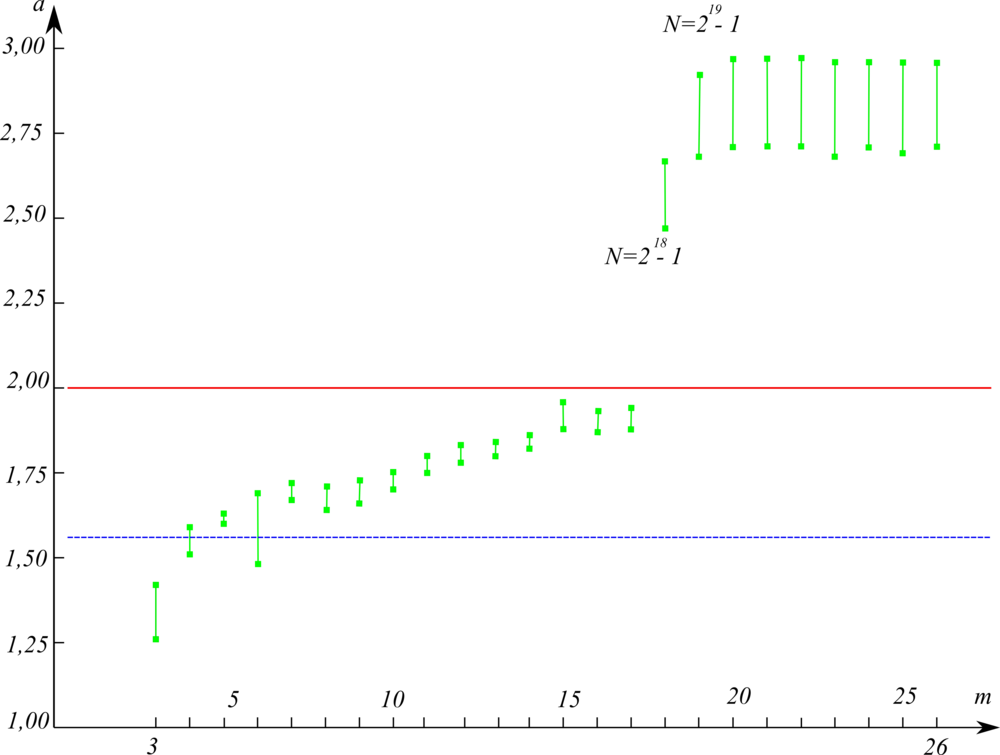
По графу видно, что, хотя и налицо "местная" локальность по вычислениям, но от яруса к ярусу расстояние между запрашиваемыми данными растёт от первых и последних ярусов алгоритма к его середине, являющимся не только узким местом алгоритма, но и имеющим наибольшую длину передачи данных между устройствами. Поэтому, хотя в циклической редукции нет той избыточной локальности, которая притормаживает работу прогонки, это преимущество, как показали замеры[1] (см. Рисунок 1), не способно компенсировать недостатки общей локальности графа циклической редукции.
2.1 Локальность реализации алгоритма
2.1.1 Структура обращений в память и качественная оценка локальности
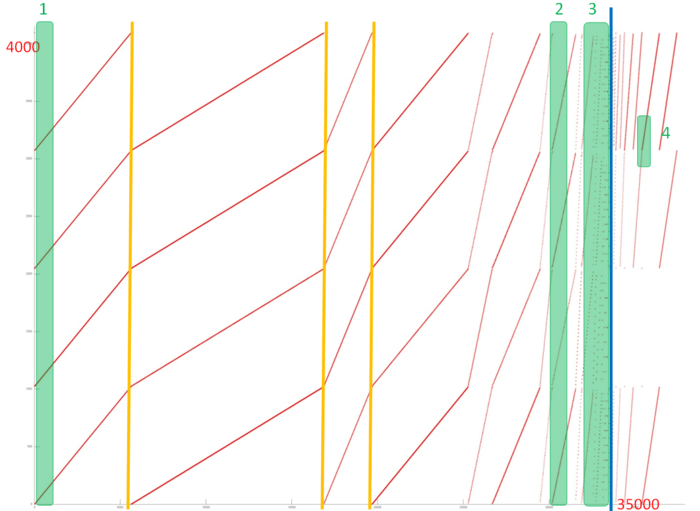
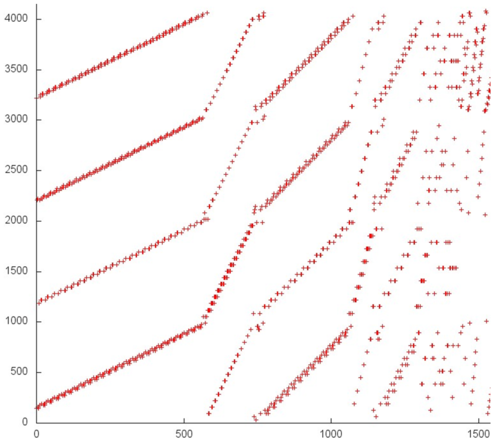
На рис. 2 представлен профиль обращений в память для реализации полного метода циклической редукции. Данный профиль достаточно интересно. Как нам известно из описания самого алгоритма, он состоит из двух частей – прямого и обратного хода. На общем профиле синяя вертикальная черта отделяет эти два этапа. Рассмотрим их в отдельности.
На первом этапе явно видны отдельные итерации (первые 3 итерации разделены желтыми линиями), каждая из которых состоит из 4 параллельно выполняемых переборов данных. Отметим, что на каждой итерации в рамках каждого перебора задействованы данные из одного и того же диапазона. Число обращений в память в каждой итерации различается, и это позволяет предположить, что характер переборов также может отличаться.
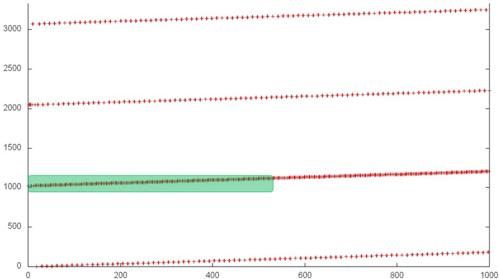
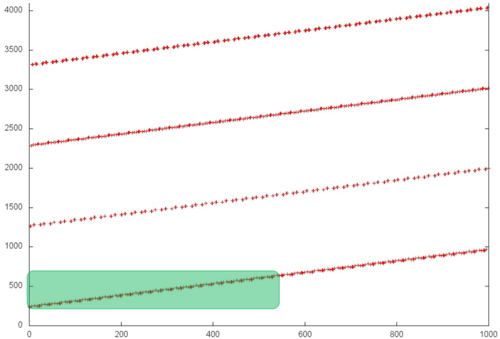
Рассмотрим фрагменты двух итераций более детально. На рис. 3 и 4 соответственно представлены фрагменты 1 и 2, обозначенные на рис. 2 зеленым. Данные фрагменты содержат по 1000 обращений. Можно увидеть, что в целом все переборы в двух фрагментах выполняются с регулярным и достаточно небольшим шагом по памяти, однако интенсивность обращений в каждом случае разная. Причем при смене итерации меняется и интенсивность обращений к одному и тому диапазону данных.
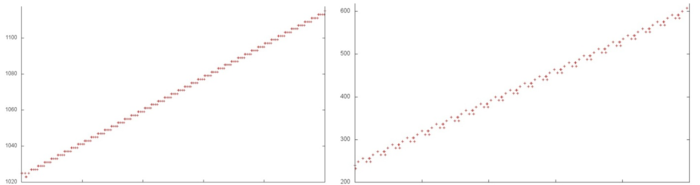
Рассмотрим еще более детально небольшие части данных фрагментов, чтобы дальше проанализировать структуру представленных переборов. На рис. 5 представлены небольшие локальные области, выделенные зеленым на рис. 3 и 4. Можно увидеть, что локальная структура обращений в целом отличается. В частности, в области, выделенной на рис. 4, шаг по памяти больше, а также выполняется меньше повторных обращений, что говорит о более низкой пространственной локальности.
В целом можно сказать, что структура итераций похожа, однако локальность несколько отличается в силу указанных выше причин. Если же говорить в среднем, такое строение итераций характеризуется от средней до высокой (в зависимости от локальной структуры) пространственной локальностью и низкой временной локальностью, поскольку данные перебираются подряд (обычно с небольшим шагом по памяти), но при этом повторно почти не используются. Отметим, что размер итераций достаточно велик, так что повторное обращение к данным на следующей итерации не приводит к улучшению локальности.
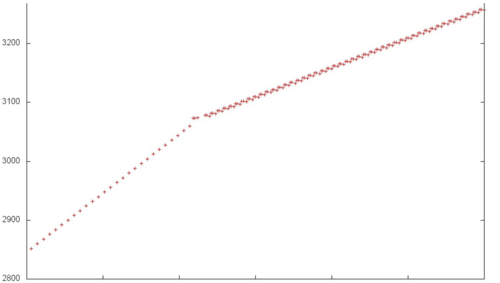
Отдельно рассмотрим самый конец первого этапа (фрагмент 3 на рис. 2), который показан на рис. 6. Здесь локальность обращений в память самая низкая, поскольку шаг по памяти в переборах становится наибольшим. В центре рисунка можно заметить область особенно низкой локальности (наиболее разрозненные обращения). Хотя данный фрагмент небольшого размера, он может серьезно снижать общую производительность взаимодействия с памятью.
Второй этап также имеет регулярную структуру. Рассмотрим на рис. 7 небольшую область более детально (фрагмент 4 на рис. 2). Из данного рисунка видно, что здесь также выполняются последовательные переборы, локальная структура которых может отличаться. Как и в рассмотренном на первом этапе случае, это приводит к различиям по пространственной и временной локальности. Стоит отметить, что угол наклона переборов на втором этапе в целом больше, чем на первом этапе (см. рис. 2), что говорит о большем шаге по памяти, и, как следствие, более низкой пространственной локальности, однако это различие может нивелироваться различиями в локальной структуре.
В целом можно сказать, что общий профиль обладает низкой временной локальностью. Пространственная локальность, скорее всего, не очень высокая, в частности, из-за неэффективной области в конце первого этапа. Однако делать предположения относительно пространственной локальности в данном случае достаточно сложно ввиду большого разнообразия локальных структур переборов.
2.1.2 Количественная оценка локальности
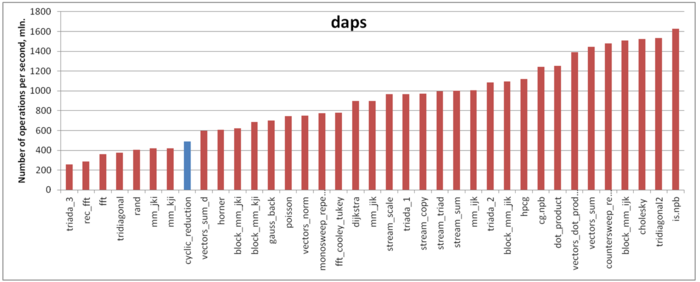
Оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.
На рисунке 8 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что производительность работы с памятью в данном случае низка и лишь чуть выше значения daps для такой неэффективной с точки зрения работы с памятью программы как тест RandomAccess (rand). В целом это соотносится с выводами, которые были сделаны нами ранее
3 Масштабируемость алгоритма и его реализации
3.1 Масштабируемость алгоритма
3.2 Масштабируемость реализации алгоритма
4 Динамические характеристики и эффективность реализации алгоритма
5 Результаты прогонов
6 Литература
- ↑ Фролов Н.А., Фролов А.В. Экспериментальные исследования влияния степени локальности алгоритмов на их быстродействие на примере решения трёхдиагональных СЛАУ // Труды 59й научной конференции МФТИ (21–26 ноября 2016 г., гг. Москва-Долгопрудный).